焊接温度场的数值求解方法

1.5.3.1 几种焊接温度场的数值求解常用热源模型（表1.5-4）

表1.5-4 几种焊接温度场的数值求解常用热源模型

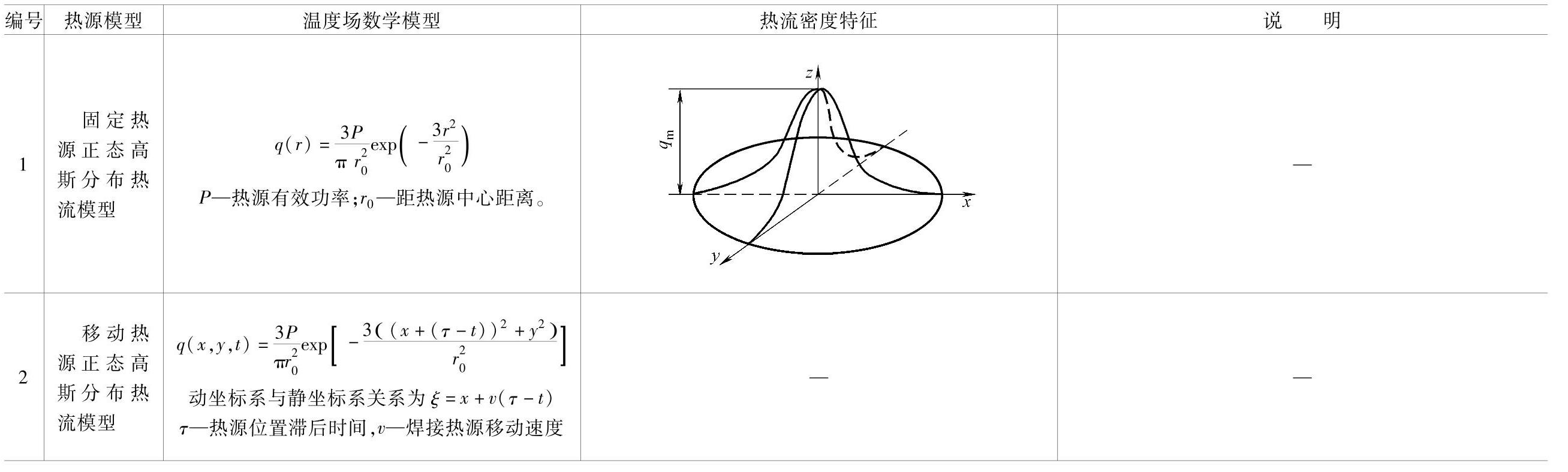
（续）

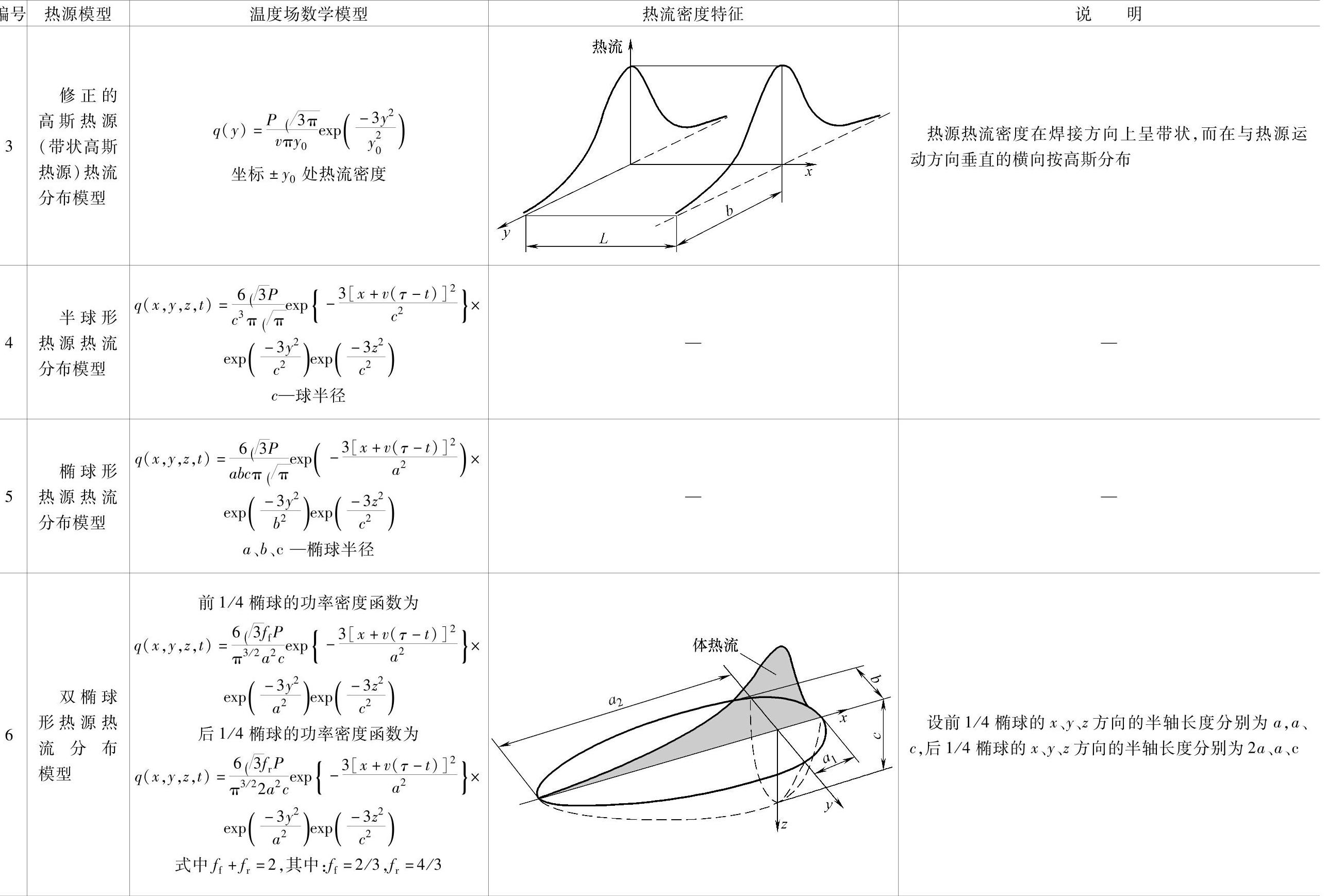
（续）

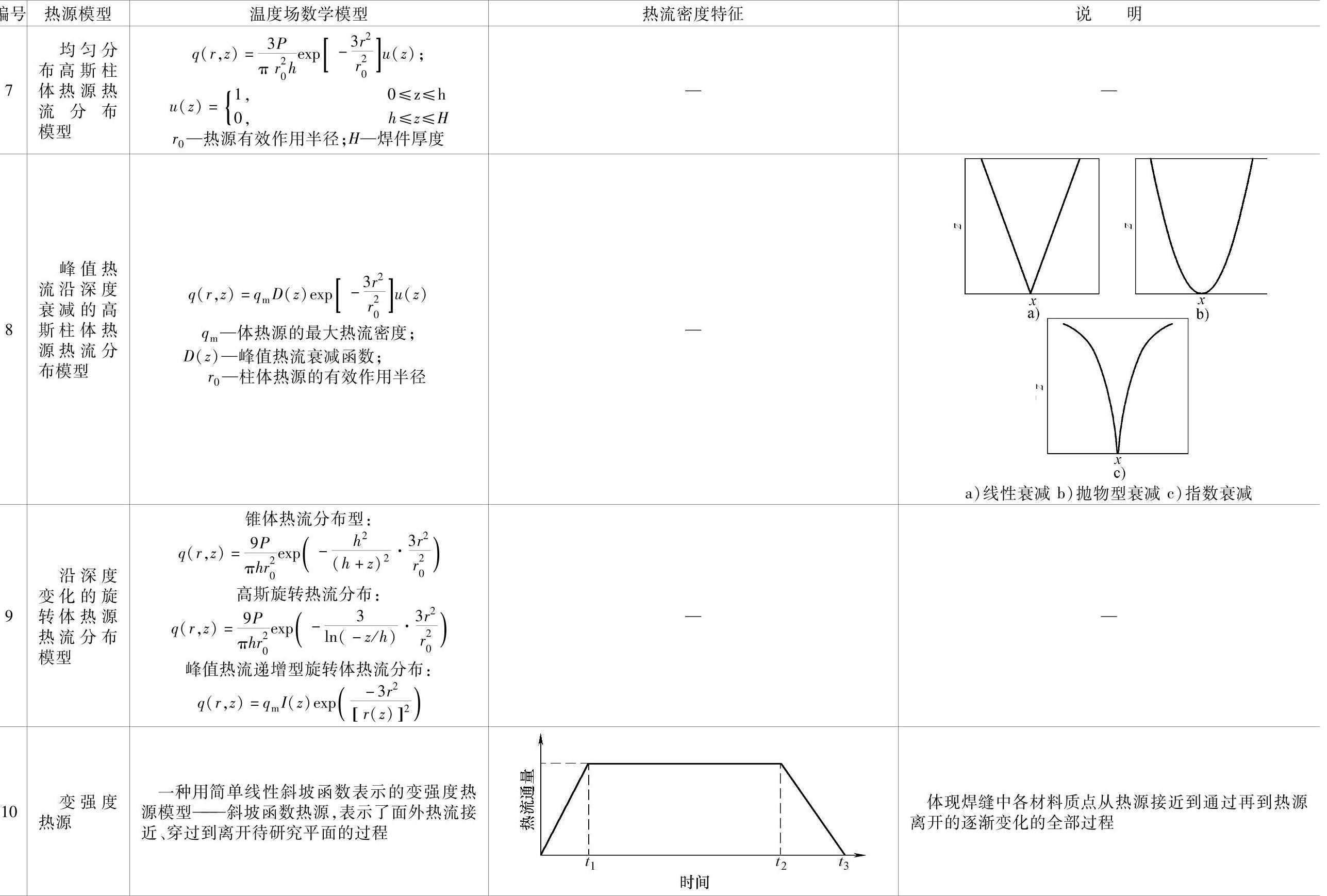
1.5.3.2几种新型组合热源热流分布模型

1.用于小孔成形深熔焊的组合热源模型

一般采用面热源和体热源两种热源相结合构成组合热源模型。表面热源一般取高斯型热流分布面热源模型，而体热源一般取峰值热流递增的旋转体热源。图1.5-2所示为一种用于激光焊和电子束焊等深熔焊的组合热源模型。

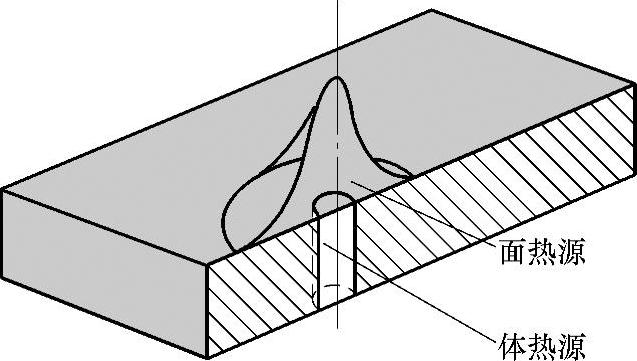
图1.5-2 面热源和体热源构成的组合热源模型示意图

面热源与体热源的总功率之和与焊接的有效功率P相当，即

P_S+P_V=P （1.5-1）

式中 P_S、P_V——面热源、体热源的功率。

将面热源功率所占总有效输入功率的比例系数称为功率分配系数，用γ表示，则有：

P_S=γP，P_V=（1-γ）P （1.5-2）

能量分配系数的取值主要取决于离焦量、热扩散系数以及焊接速度等。

将给定的面热源功率及体热源功率代入相应的高斯面热源功率密度分布模型和旋转体热源功率密度分布模型，就可以得到相应的组合热源模型。

2.用于T形接头的激光+GMAW复合热源模型

该热源模型需要考虑接头几何形状和GMAW焊枪倾角对热流分布的影响。为此，需要构建适合于描述激光焊接和GMAW的复合热源。图1.5-3为激光+GMAW复合焊接T形接头结构示意图。

图1.5-3 激光+GMAW复合焊T形接头结构示意图

θ—GMAW焊枪倾角

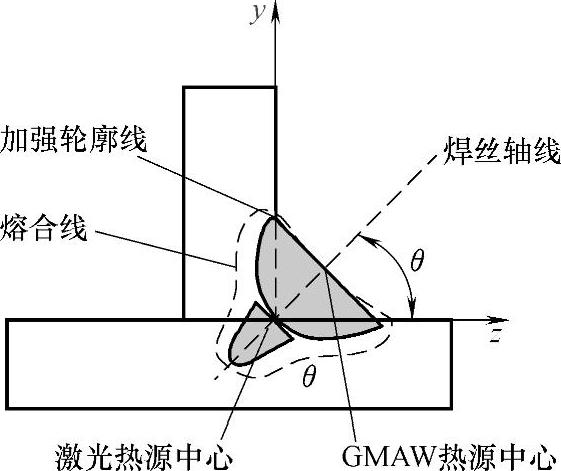
图1.5-4 热源作用位置示意图

GMAW热源采用双椭球体热源模型描述，并且考虑了短路峰值和背弧电流参数，由于焊枪倾角的存在，使用了坐标旋转。GMAW热源中心位于角接头表面中间位置，如图1.5-4所示。此种情况下的热流分布可表示为

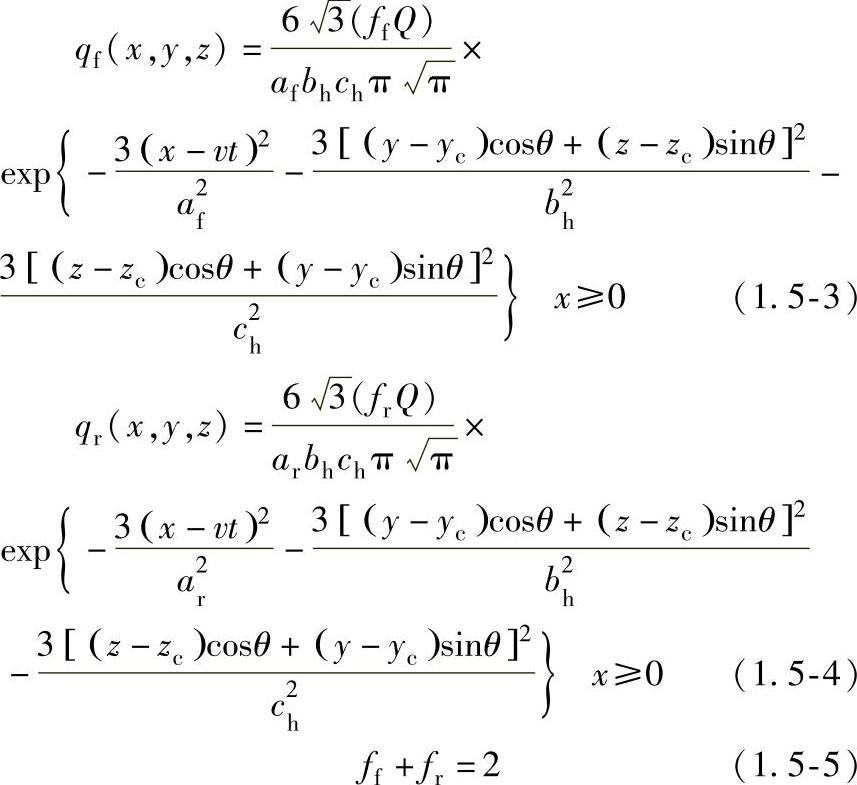
式中 q_f和q_r——热源中心前、后热流分布函数；

Q——GMAW有效热输入，在峰值和背弧期间其值不同；

v——焊接速度；

a_f、a_r、b_h、c_h——分布参数；

t——时间；

y_c，z_c——热源中心坐标；

θ——焊枪与T形接头平板之间夹角；

f_f、f_r——热流分配系数。

激光焊接用旋转体热源模型描述其峰值热流密度和分布半径沿厚度方向变化。热作用半径沿厚度线性递减而峰值密度按指数增加。由于角焊缝的接头形状，激光热源模型也采用了坐标旋转。激光焊接热源中心位于角接头根部位置（图1.5-4）。此种情况下的激光焊接热流分布可表示为

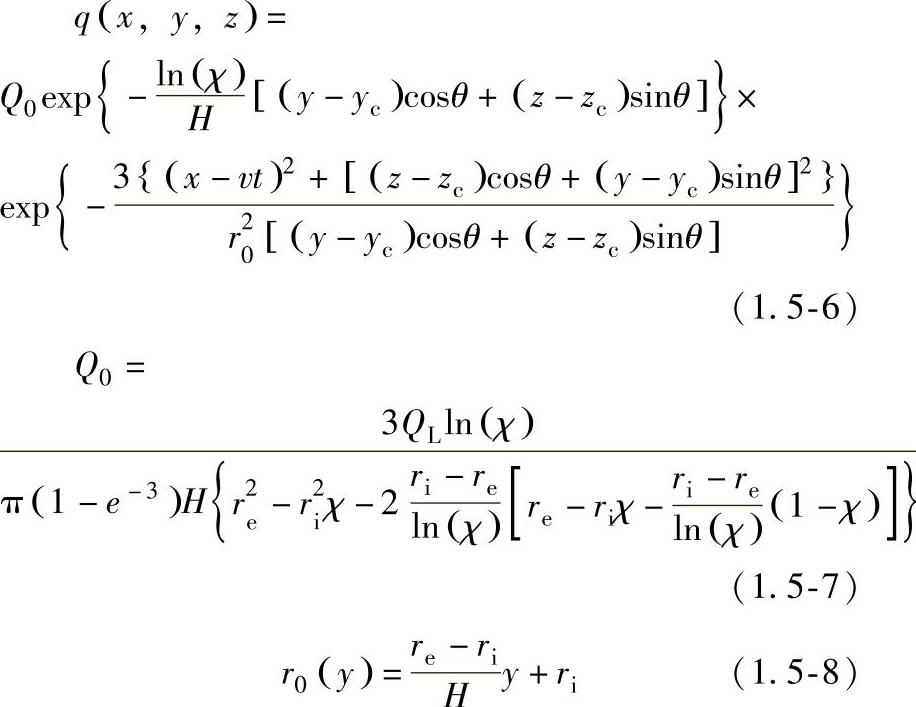
式中q（x，y，z）——激光热源热流分布函数；

H——热源高度；

r_e、r_i——热源上表面和下表面半径；

χ——上、下表面峰值功率密度分配系数；

r₀（y）——热源半径变化函数；

Q_L——激光有效功率。

将上述两个描述GMAW焊接和激光焊接的子模型复合，即构成了总的T形接头的激光+GMAW复合热源模型。而两个子模型间的相互作用，可间接地通过适当调整一些分布参数予以考虑。

1.5.3.3 焊接热传导温度场的数值模拟

1.考虑Stefan问题的运动金属薄板激光焊温度场求解

（1）基本模型和计算条件 设有一厚度为h的金属薄板，以v速度运动，上表面受功率为W的激光加热。当激光功率达到某一临界值W_cr时，局部会发生熔化。焊接材料选取于不锈钢，所以熔化过程材料密度变化很小，可认为整个焊接中金属板以恒定的速度v和密度ρ运动。对于微连接来说，熔化区域非常小（L_m≈100～300μm），意味着熔化金属在表面张力作用下处于一薄层状态。

焊接过程如图1.5-5所示，固体金属在小孔轮廓线K的左半部分被熔化，而后以液态连续流动至右侧的熔化边界，在此，金属由液态凝固成固态。金属在经过轮廓线K时，隐性热量γ被释放（凝固过程）或吸收（熔化过程）。材料的热物理性能在跨越固液边界K时是不连续的，热通量是连续的。

以焓H（J/kg）和热通量q（W/m²）表示的能量守恒方程为

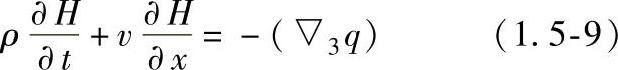
式中 ▽₃——梯度的三维运算符号；

q——热流密度。

q=-λ▽₃T （1.5-10）

式中 λ——导热系数；

T——温度。

图1.5-5 激光焊接加热与熔化过程示意图

如果板厚h小于激光束半径r_b，则厚度方向的温度变化很小，因此三维问题可简化为二维问题，设激光束功率密度服从高斯分布，则能量守恒方程可写为

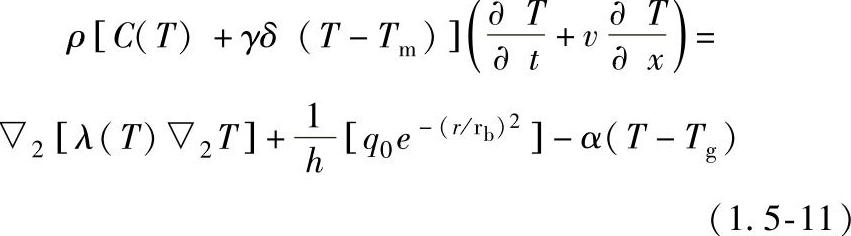
计算模型如图1.5-6所示。

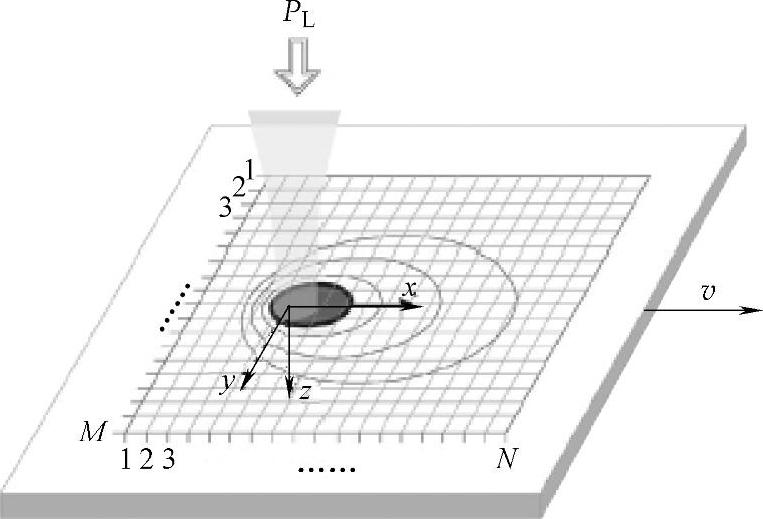
图1.5-6 计算模型示意图

（2）Stenfan问题的考虑 对于具体的焊接金属材料，熔化轮廓线K应该是熔化温度T_m（对于不锈钢T_m=1460℃），但其位置是不知道的，必须计算确定。

设材料热导率、比焓与温度的关系如图1.5-7所示。在熔化温度T_m，液态的焓值H_L比固态的焓值H_S大γ。这种焓值的跳变可用δ函数来表示：

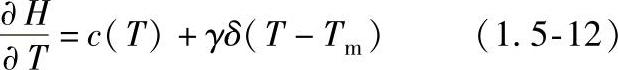
式中c（T）——比热容。

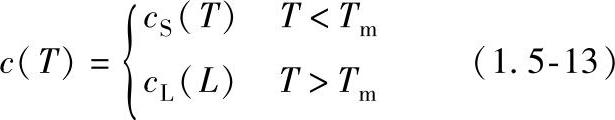
图1.5-7 计算材料热导率和比焓与温度的关系示意图

Stefan问题数值求解的有效算法是发生在相变温度的阶跃热物理量的光滑处理，即将δ函数用有限宽和有限大的光滑函数代替，因此c（T）和λ（T）可写成：

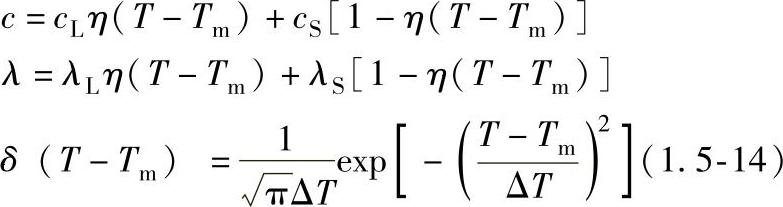
式中：

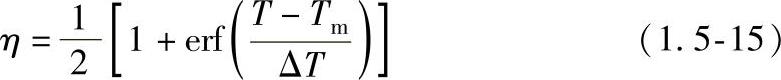
ΔT用以说明相变特征温度。为了避免计算过程的不稳定性，ΔT既不能取得过小，又不能取得过大。在不锈钢激光焊时ΔT=50～100℃。

（3）计算结果取不锈钢焊接材料的热物理参数为：

c_S=465J/kg，c_L=550J/kg，λ_S=20W/（K·m²），λ_L=40W/（K·m²），ρ=7.8×10³kg/m³，γ=277×10³J/kg，T_m=1460℃。

板厚h=25×10^-6m，板的移动速度v=0.1m/s；激光功率W_L=10W，激光束半径r_b=50×10^-6m，环境温度T_g=25℃；传热系数α=10³W/（K·m²）。

按二维模型计算。图1.5-8所示为考虑熔化和不考虑熔化时，计算所得温度在y=0线上的分布。图1.5-9所示为考虑熔化和不考虑熔化时，计算所得温度场分布。

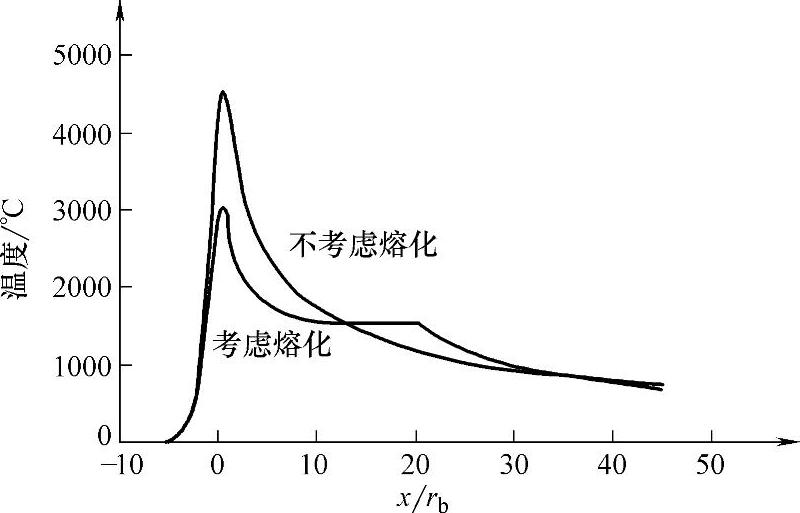
图1.5-8 按二维模型计算所得温度在y=0线上的分布

设板厚h=100×10^-6m，按三维模型计算。图1.5-10所示为考虑熔化和不考虑熔化时，计算所得板厚上、下表面y=0线上的温度分布。可见即使在考虑熔化情况下，上表面最高温度也达3000℃，大大超过了材料的汽化温度。为了表明汽化情况，计算中取最高温度为汽化温度T_max=T_e=2725℃，图1.5-11所示为考虑汽化作用的Stefan问题求解温度分布。

图1.5-12和图1.5-13所示为计算所得熔化区域几何参数随激光输入功率的变化情况。

图1.5-14所示为计算的焊道断面尺寸与实际焊道尺寸比较。

2.管道在役熔透焊接温度场计算

管线钢在役焊接采用“摆动”焊条电弧焊，可以获得较浅的熔化深度，因此热源强度分布比高斯分布更为平坦，这种效应可通过改变双椭圆形高斯热源分布来获得，数学表示如下：

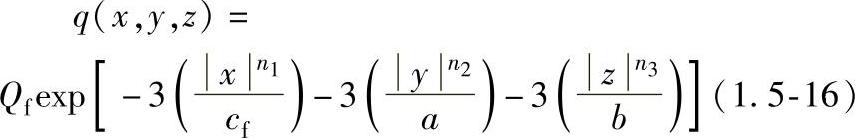
此时，热流密度分布不再是椭圆形，可用如下的方程表示：

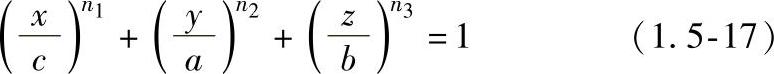
Q_f可通过数值积分来求得：

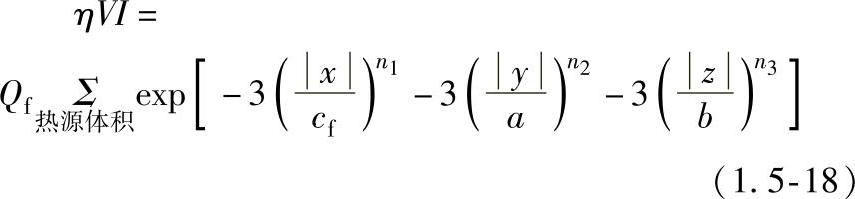
图1.5-15 所示为高斯热流分布（n₁=2，n₂=2）与非高斯热流分布（n₁=2，n₂=10）比较。计算实体模型和坐标系如图1.5-16所示。

图1.5-9 考虑熔化和不考虑熔化时，二维情况计算所得温度场分布

a）考虑熔化 b）不考虑熔化

图1.5-10 按三维模型计算所得温度在y=0线上的分布

注：线性模型是不考虑熔化，Stefan问题是考虑熔化。

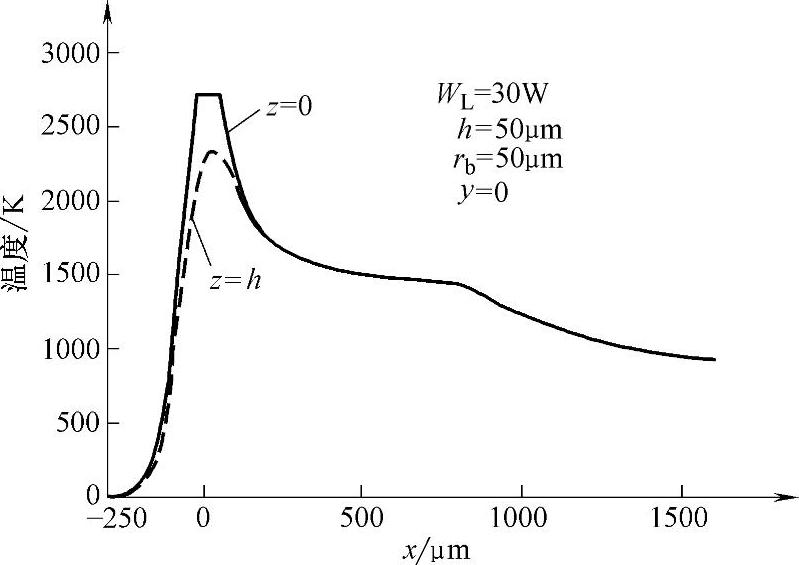
图1.5-11 考虑汽化作用的Stefan问题求解温度分布

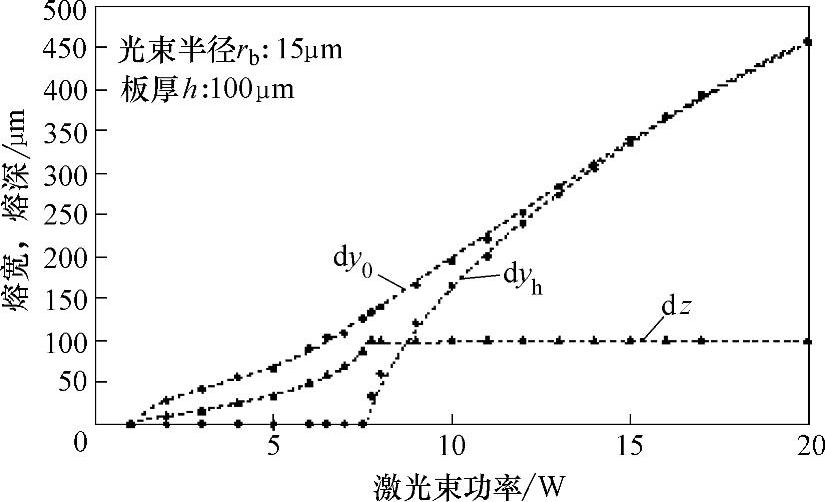
图1.5-12 光束半径r_b为15μm情况下，熔化区域几何参数与激束功率的关系

dy₀—上表面熔宽 dy_h—下表面熔宽 dz—熔深

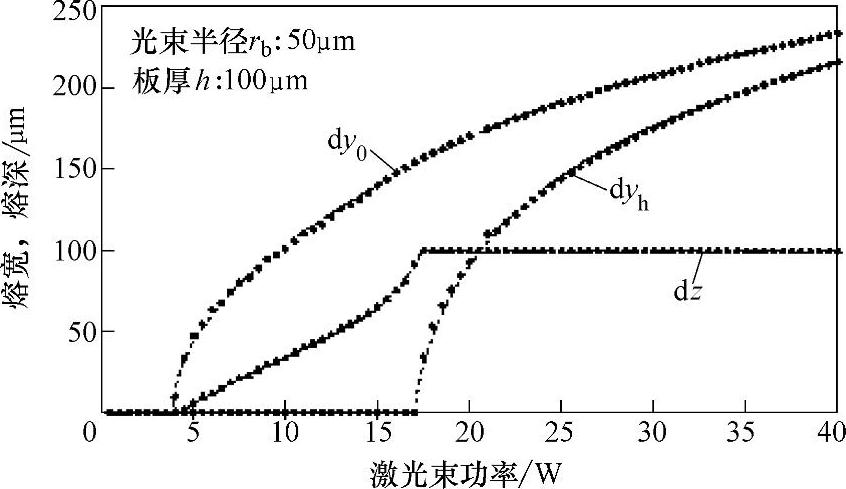
图1.5-13 光束半径r_b为50μm情况下，熔化区域几何参数与激光束功率的关系

dy₀—上表面熔宽 dy_h—下表面熔宽 dz—熔深

采用三维有限元方法计算。除管道内表面外，模拟实体其他表面对流传热系数取h_c=0.12×10^-4W/（m²·K），辐射热损失忽略不计。材料热物理参数与温度有关，但与微观组织无关。焊接参数、管体几何参数和流动条件由爱迪生焊接实验室的试验给出，模拟计算用来给出焊缝t_8/5冷却时间。图1.5-17和图1.5-18所示为计算的瞬态温度场和t_8/5冷却时间。

3.钛合金薄板带热沉的TIG焊温度场

采用三维有限元数值模拟钛合金TC4薄板焊接过程中的温度场。以低应力无变形焊接法为对象，系统构成如图1.5-19所示。

（1）计算模型 TC4钛合金平板试件的尺寸为320mm×300mm×2mm。有限元网格如图1.5-20所示，其中最小单元尺寸为1mm×1mm×2mm，共有3460个单元，7292个节点。

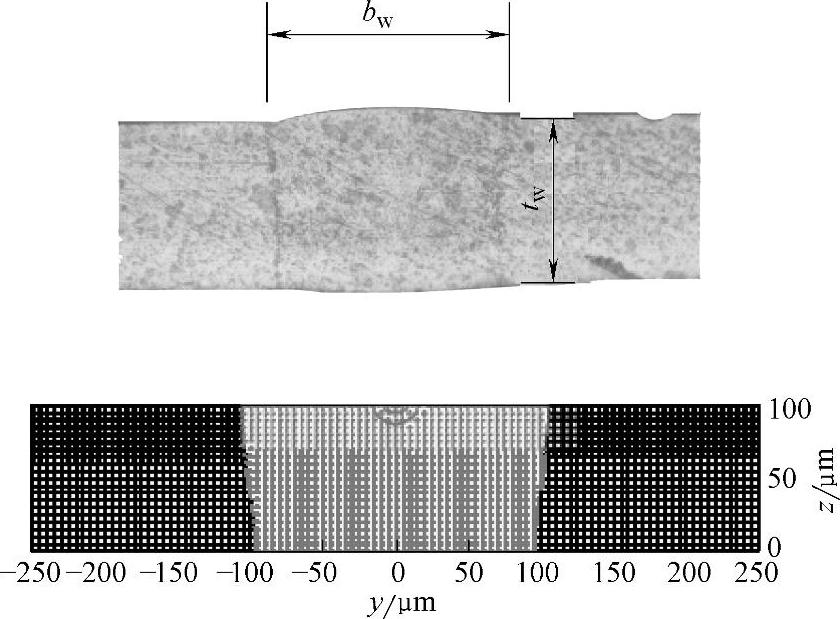
图1.5-14 计算的焊道断面尺寸与实际焊道尺寸比较 b_w=150μmt_w=100μm

图1.5-15 z=0平面的热流密度分布

a）n₁=2，n₂=2 b）n₁=2，n₂=10

图1.5-16 计算实体模型和坐标系

a）圆周角焊缝 b）马鞍形坡口焊缝

图1.5-17 计算所得t=4s时的瞬态温度场分布

注：b）为a）的局部放大图。

图1.5-18 三维瞬态模型计算、三维准稳态模型计算和试验测定的t_8/5冷却时间比较

图1.5-19 动态控制低应力无变形焊接装置示意图

1—冷却喷嘴 2—焊嘴 3—夹具 4—焊件 5—垫板

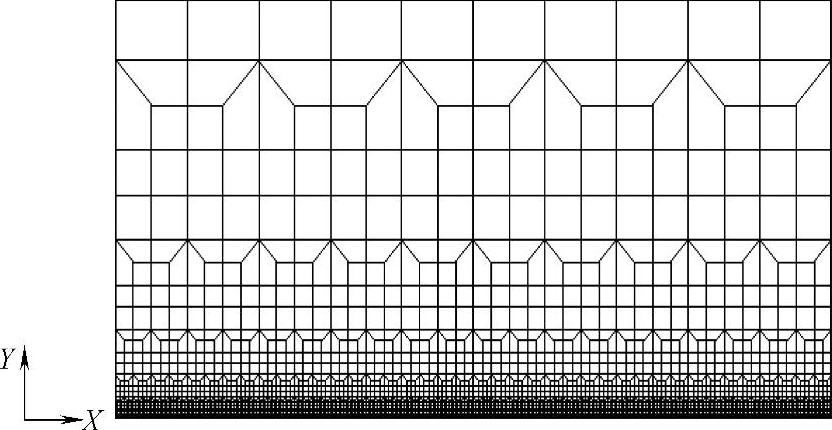
图1.5-20 有限元网格

（2）热源及热沉模型 焊接电弧的热流分布按高斯模型描述。焊接过程中热沉的冷却介质采用氩气雾化冷却水，在有限元数值计算中，试件与雾化冷却水之间的换热以单个圆形射流冲击传热模型来模拟。在数值计算中热沉和热源都以一定的焊接速度移动。

（3）计算参数 对常规和添加辅助热沉的自动钨极氩弧焊分别进行有限元分析。焊接电流I=200A，焊接电压U=10V，焊接热源的热效率取η=47.8%，试件背面无铜垫板。热源及热沉的行走速度均为3.5mm/s，两者中心相距25mm。热沉冷却介质喷嘴直径D为1.3mm，冷却介质流量为280mL/min，除热沉外，常规焊与动态低应力无变形焊接（DC-LSND焊）数值模拟的工艺参数均相同，计算以TC4钛合金为对象，材料热物性参数是温度的函数。

（4）计算结果及分析 图1.5-21所示为常规焊和DC-LSND焊温度场，表示了焊接进行至62.5s，电弧中心行走至x=219mm时，上表面的温度场分布。

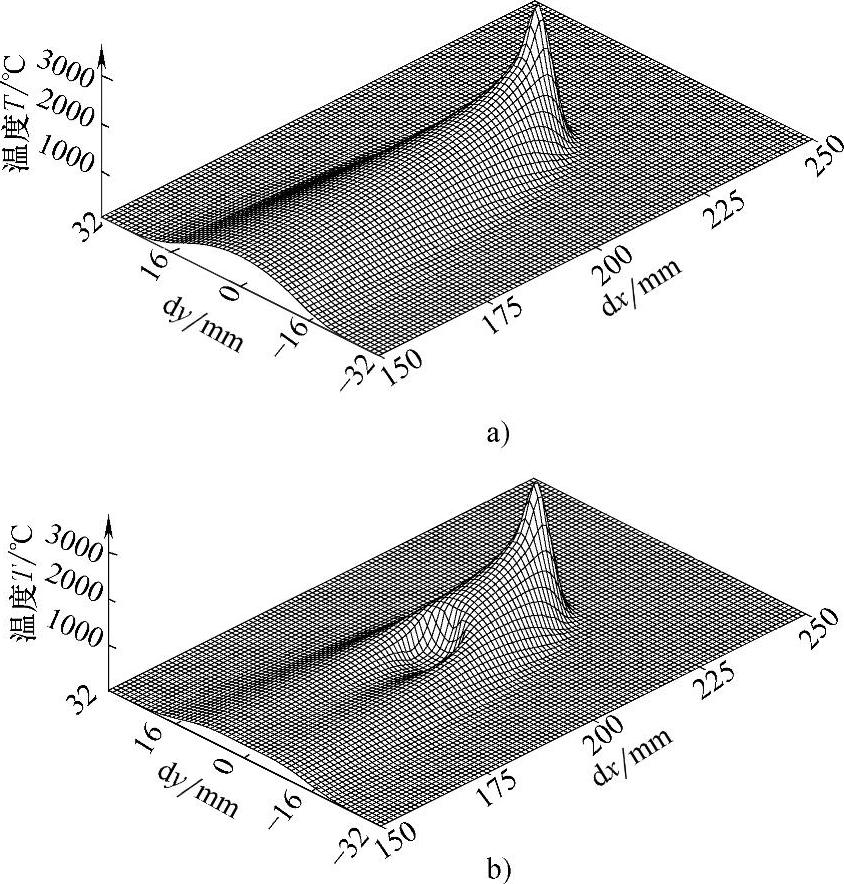
图1.5-21 常规焊和DC-LSND焊温度场

a）常规焊上表面温度分布 b）DC-LSND焊上表面温度分布

图1.5-22所示为常规焊及DC-LSND焊进行至62.5s时的等温线。

图1.5-23所示为常规焊和DC-LSND焊接过程中位于x=192mm的横断面上，距焊缝中心线的距离分别为0mm、3mm、5mm、10mm、16mm时的热循环曲线。

1.5.3.4 焊接熔池流体流动和传热过程数值模拟

1.基本数学模型

（1）控制方程 以TIG焊熔池流体流动和传热过程作为研究对象。在电弧热源的作用下，被焊金属局部发生熔化，形成熔池。模拟熔池内的液态金属在浮力、电磁力、表面张力、电弧等离子流力的作用下产生流体流动。

基本假设：①熔池中高温金属的流动为层流、不可压缩牛顿流体；②除表面张力、比热容和热导率外，其余热物理常数与温度无关；③熔池中液态金属流动的驱动力有表面张力、浮力和电磁力，而不考虑电弧等离子体流动的拖拽力，这是由平表面假设决定的；④Boussinesq假设成立，即除浮力项外所有其他项中的密度认为是常数；⑤来源于焊接电弧的热流密度分布和电流密度分布服从高斯（Gaussian）分布。

设有一热流密度为q₀的电弧热源以恒定速度U_t沿固定坐标系（ξ，y，z）中的ξ轴移动，根据固定坐标系与动坐标系（x，y，z）的关系，x=ξ+U_tt，以及上述基本假设，可得以电弧热源中心为坐标原点的移动坐标系下熔池中流体流动和传热的控制方程组。

连续方程：

x方向动量守恒方程：

y方向动量守恒方程：

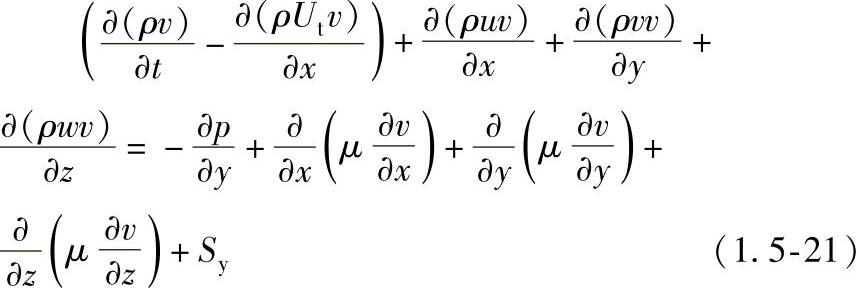
z方向动量守恒方程：

能量守恒方程：

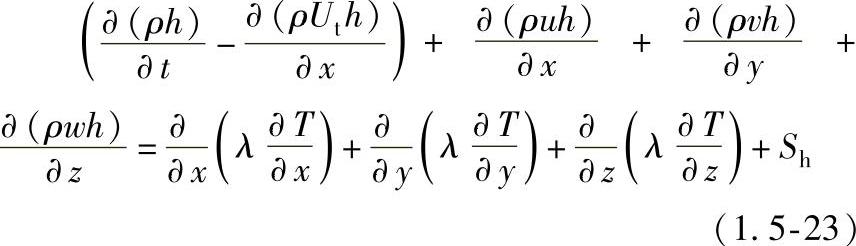
式中 u，v和w——x，y和z方向的速度；

ρ——密度；

μ——黏度；

λ——热导率；

p——压力；

h——焓；

S_x、S_y、S_z、S_h——源项。

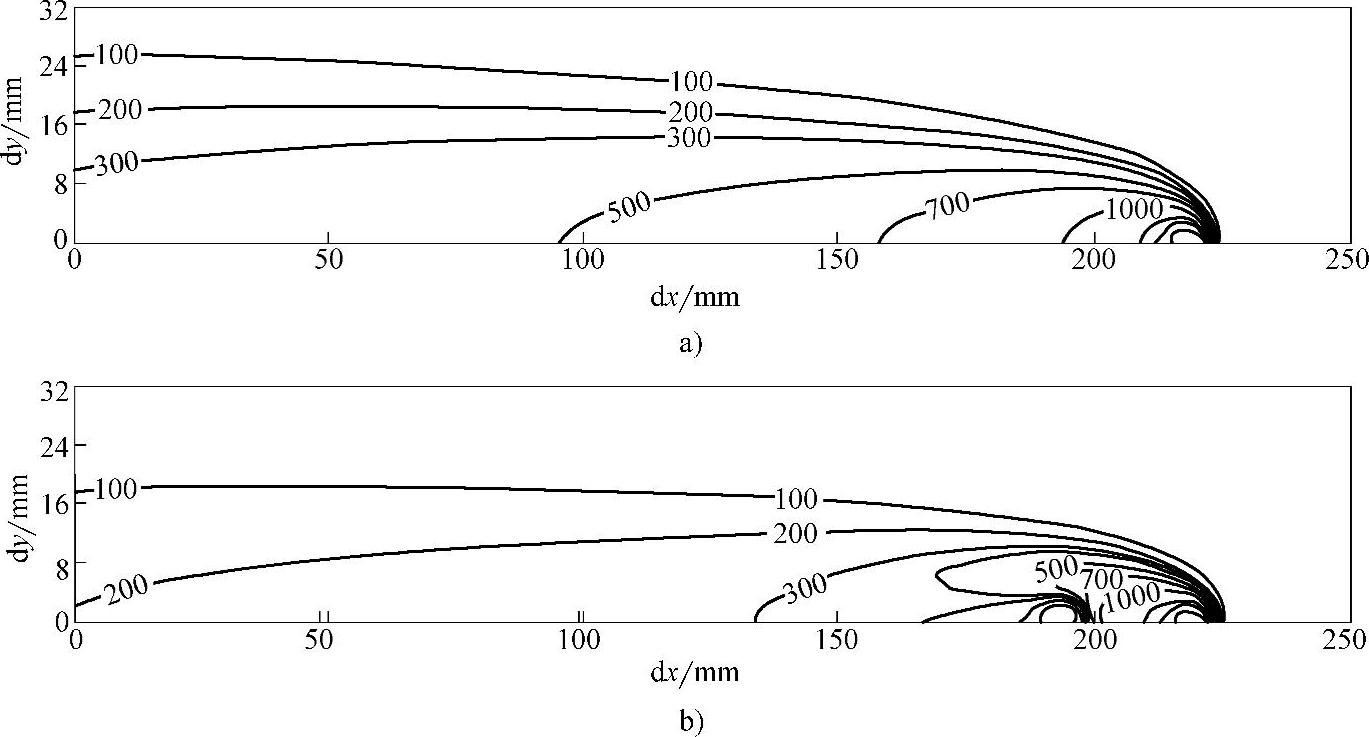
图1.5-22 常规焊和DC-LSND焊温度场等温线

a）常规焊温度场等温线 b）DC-LSND焊温场等温线

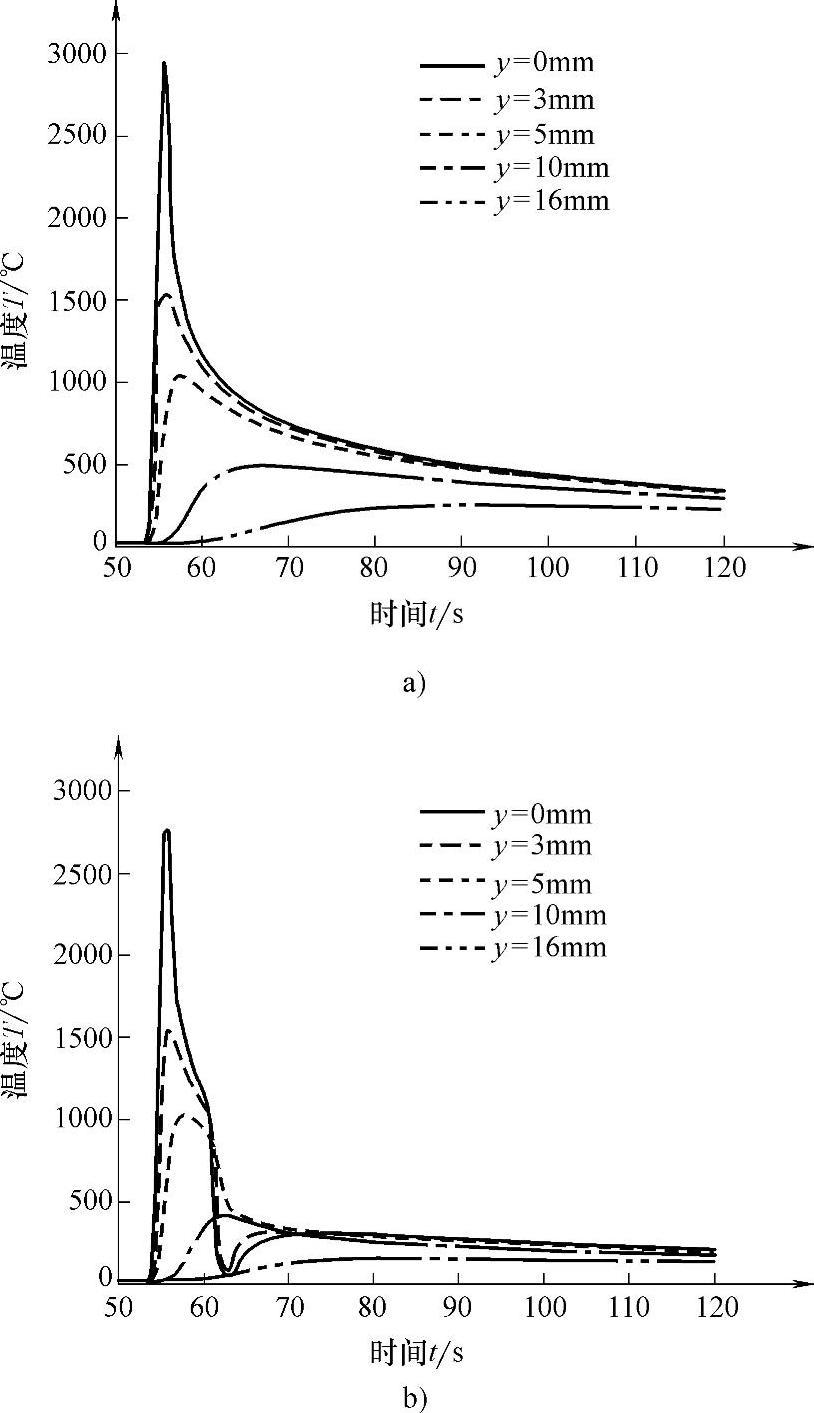
图1.5-23 距焊缝中心不同距离点的热循环

a）常规焊不同位置点的热循环 b）DC-LSND焊不同位置点的热循环

相变问题的处理采用焓-孔隙率方法，则上述动量方程的源项取如下形式：

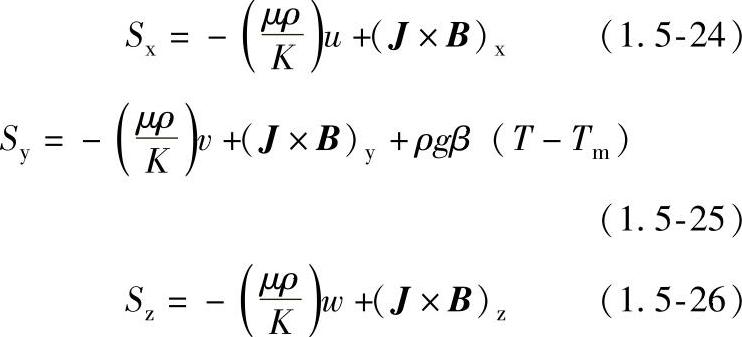
假设渗透率K仅是液相分数的函数，并且遵循Kozeny-Carman方程（1.5-27），且假设渗透率各向同性。

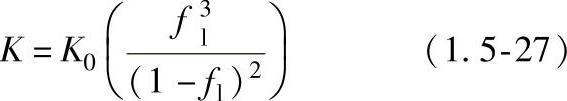
式中 K₀——与枝晶形貌有关的常数；

f_l——液相体积分数，它与温度的关系按线性化处理：

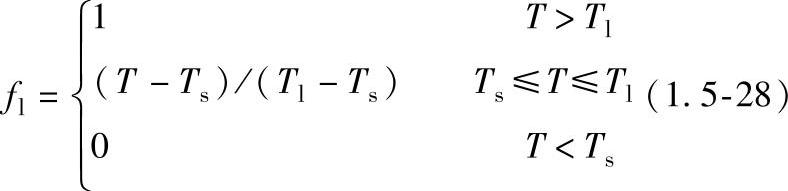
能量守恒方程（1.5-23）写成了比焓的形式：

h=（1-f_l）c_sT+f_lc_lT+ΔH （1.5-29）

式中 c_s和c_l——固相和液相比热容。

ΔH——比焓的熔解热部分，它与温度的关系为

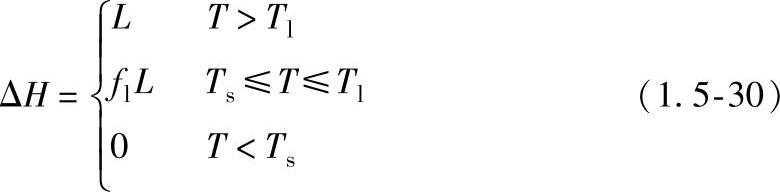
式中 L——熔热；

T_l和T_s——固相线和液相线温度。

（2）电磁力的计算式（1.5-24）～式（1.5-26）中的电磁力的计算需要求解一组稳态的Maxwell方程：

▽J=0

J=-σ▽φ

▽²φ=0

▽B=μ₀J （1.5-31）

式中 J——电流密度矢量；

σ——电导率；

φ——电势；

B——磁感应强度矢量；

μ₀——磁导率。电磁力是通过J×B在x、y、z三个方向上的分量而加入到动量方程源项中的。

（3）边界条件 对于计算区域来说，（u，v，w，T）变量的边界取值如下。

上表面：

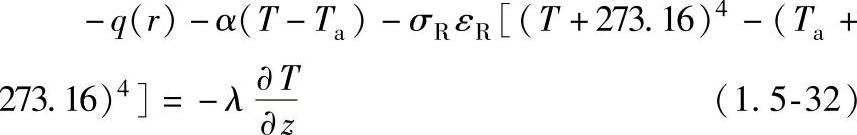
式中 α——表面传热系数；

ε_R——发射率；

σ_R——Stefan-Bolzmann常数；

T_a——环境温度。

热流密度服从高斯分布

式中r_b——有效加热半径。

电流密度也服从高斯分布

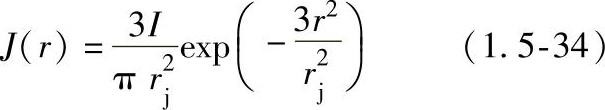
式中 r_j——电流密度分布半径。

在平表面假设条件下，表面张力按式（1.5-35）计算

式中 μ——黏度；

σ_S——表面张力温度系数。

上表面w=0。

侧表面和底表面：对流热损失条件成立

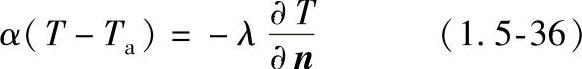
式中 n——散热面的法向单位矢量。

速度条件满足u=v=w=0。

（4）数值模拟程序的实现在对控制方程组的求解中，Patanker和Spaldig提出了一种SIMPLE（Semi-implicit method for press-linked equation）的有限差分算法。这种方法对于解速度压力耦合场非常有效。

根据稳态电流假设，电流和流体流动是相互独立的，因此首先计算电磁力，然后将其作为体积力加到动量方程中，而后耦合求解连续性方程、动量方程和能量方程。

SIMPLE算法的基本运算步骤如下：

1）给出或承接上一时间步长的速度场、温度场和压力场。

2）计算动量方程的系数，暂时在动量方程中略去压力梯度项后求解动量方程，求得一组近似的速度场。

3）将近似的速度场代入压力方程，求解近似的压力场。

4）将近似的压力场代入动量方程求解速度场u^∗、v^∗、w^∗。

5）将速度u^∗、v^∗、w^∗代入压力修正方程，求得p′，将p′代入速度修正方程修正速度场。

6）返回步骤2），重复上述过程直至收敛。

7）时间增量一个时间步长。

8）返回步骤1），直至达到预定时间。

2.激光深熔焊熔区的流体流动与传热

（1）计算模型的确立 激光深熔焊过程会形成穿透小孔，小孔周围熔化金属的复杂流动主要由表面张力、浮力以及气化金属逃逸小孔时产生的摩擦力（图1.5-24）引起。该模型中计算变量以无因次形式表示，以减少求解变量和独立分析无因次参量对熔区的影响。

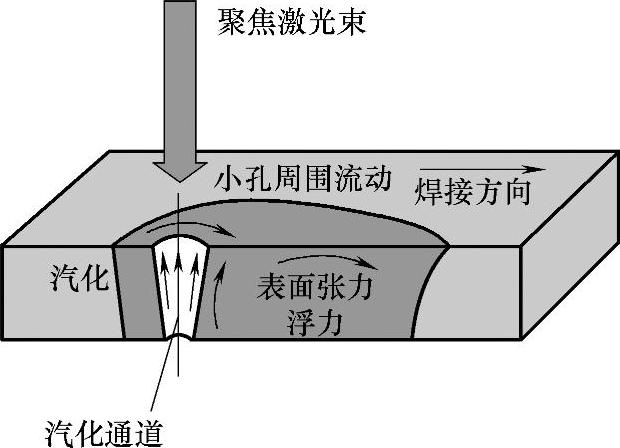
图1.5-24激光深熔焊时熔区相关现象示意图

设焊接熔池表面为平面，与激光束中心和汽化通道相关联的坐标系用极坐标（R，φ，Z）表示，计算区域包括焊接熔池和周围区域，如图1.5-25所示。在熔化区域温度与速度场耦合，而在熔池以外，速度即为焊接速度。在熔池区域，需求解能量守恒、动量守恒和质量守恒方程，以获得温度和速度分布。

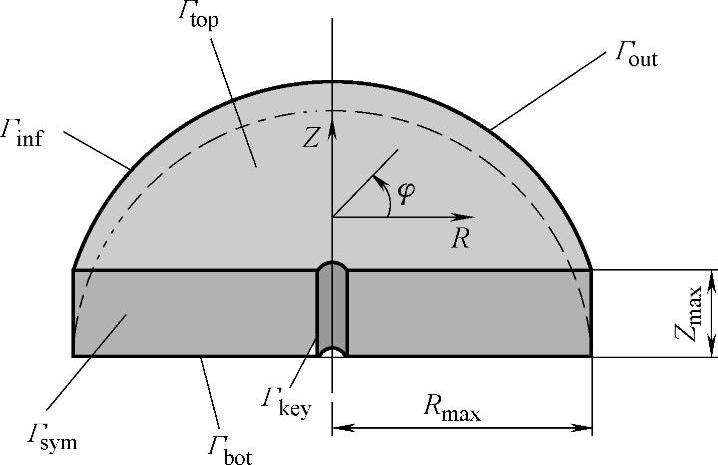
图1.5-25激光深熔焊时温度场计算区域示意图

控制方程组和边界条件用有限差分法求解，图1.5-26所示为小孔附近非均匀网格划分情况。

图1.5-26小孔周围的网格划分

（2）控制方程与边界条件 用无因次形式表示的控制方程组如下：

能量方程：

动量方程：

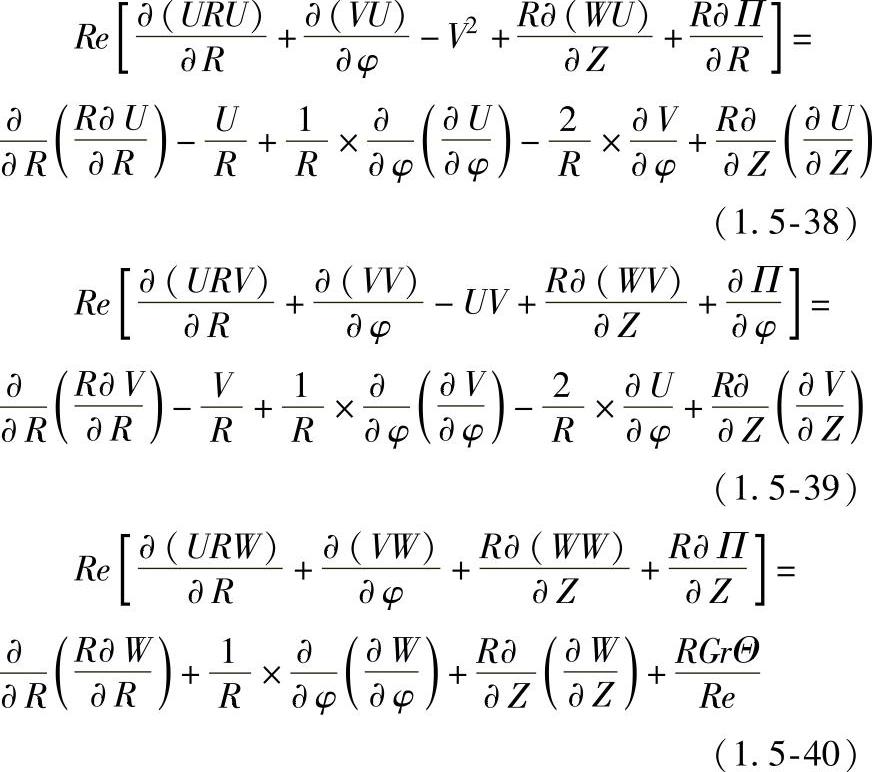
连续方程：

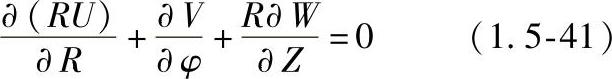
式中 Pe——贝克莱数；

Re——雷诺数；

Gr——格拉晓夫数，三者关系为。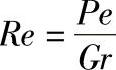

无因次温度定义为：Θ=（θ-θ_u）/（θ_v-θ_u）

式中 θ_v——汽化温度；

θ_u——环境温度。

无因次压力定义为：Π=p/（ρ₀v²₀）(www.xing528.com)

式中 v₀——焊接速度；

U，V，W——用焊接速度v₀处理的无因次速度。

边界条件为

熔化区以外的速度等于焊件的运动速度；小孔表面温度等于汽化温度；熔化区材料热物理参量，密度ρ^∗、比热容c^∗、热导率λ^∗取平均值，而与温度无关，只考虑它们在固态下与温度的关系；熔解热L的影响通过增加比热容来考虑：

当活性元素存在时，表面张力温度系数是活性元素含量和温度的函数。对于二元合金系，表面张力与温度和活性元素含量的关系可表示为

式中 A——常数；

R——气体常数；

γ_m——纯金属在熔化温度T_m时的表面张力；

k₁——与偏聚熵有关的常数；

ΔH⁰——标准吸附热；

a_i——表面活性元素的活度（质量分数）；

——第i种活性元素的局部摩尔能；

Γ_s——饱和表面过剩值；

K_seg——氧元素平衡吸附系数。

表面张力温度系数的公式可表示为

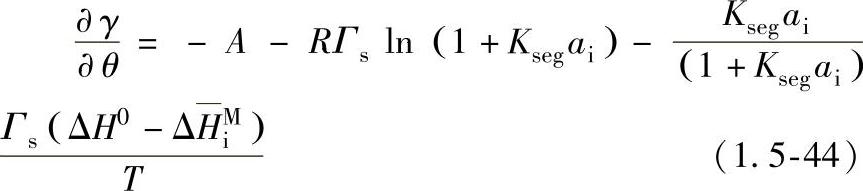
∂γ/∂θ是温度和活性元素含量的函数。纯金属时，∂γ/∂θ为负值。含有表面活性元素的合金体系中，∂γ/∂θ与温度T、平衡偏聚常数K_seg、表面活性元素的含量a_i有关。

该计算中只考虑活性元素硫的影响，图1.5-27所示为不同硫含量情况下，Fe-S系中表面张力温度系数与温度的关系。

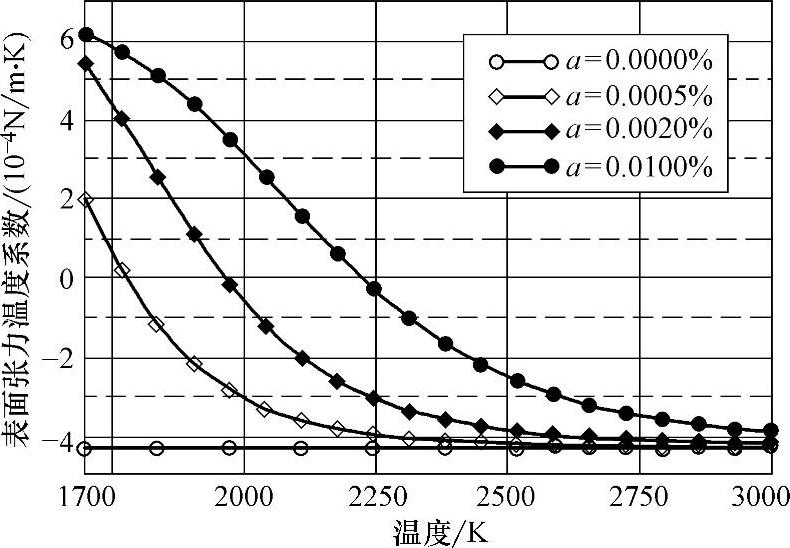
图1.5-27 不同硫含量情况下，Fe-S系中表面张力温度系数与温度的关系

（3）计算结果 对于一个确定的材料，密度ρ、比热容c、热导率λ，无因次熔化温度Θ_m和相变数Ph为已知，则无因次温度Θ（R，φ，Z）仅是特征参量Pe、Pr、Re、Gr、Ma、W_key和Z_max的函数。无因次变量的定义如下：

为了考察不同变量对熔区的影响，计算中将其他参量保持不变，而仅改变一个参量。首先，设Ma=Gr=W_key=0，则意味着忽略表面张力、浮力、摩擦力。这种情况下，无因次温度是二维的，仅与Pe有关。

图1.5-28所示为Pe=1和Pe=4，无因次熔化温度Θ_m=0.5和Pr=0.1情况下计算的无因次温度场和速度场。

图1.5-29所示为浮力、表面张力和摩擦力单独因素影响的计算结果，Pe=0.1、Pr=0.1、Θ_m=0.5、Z_max=5.0条件下，改变其他参数计算的温度场和速度场分布。

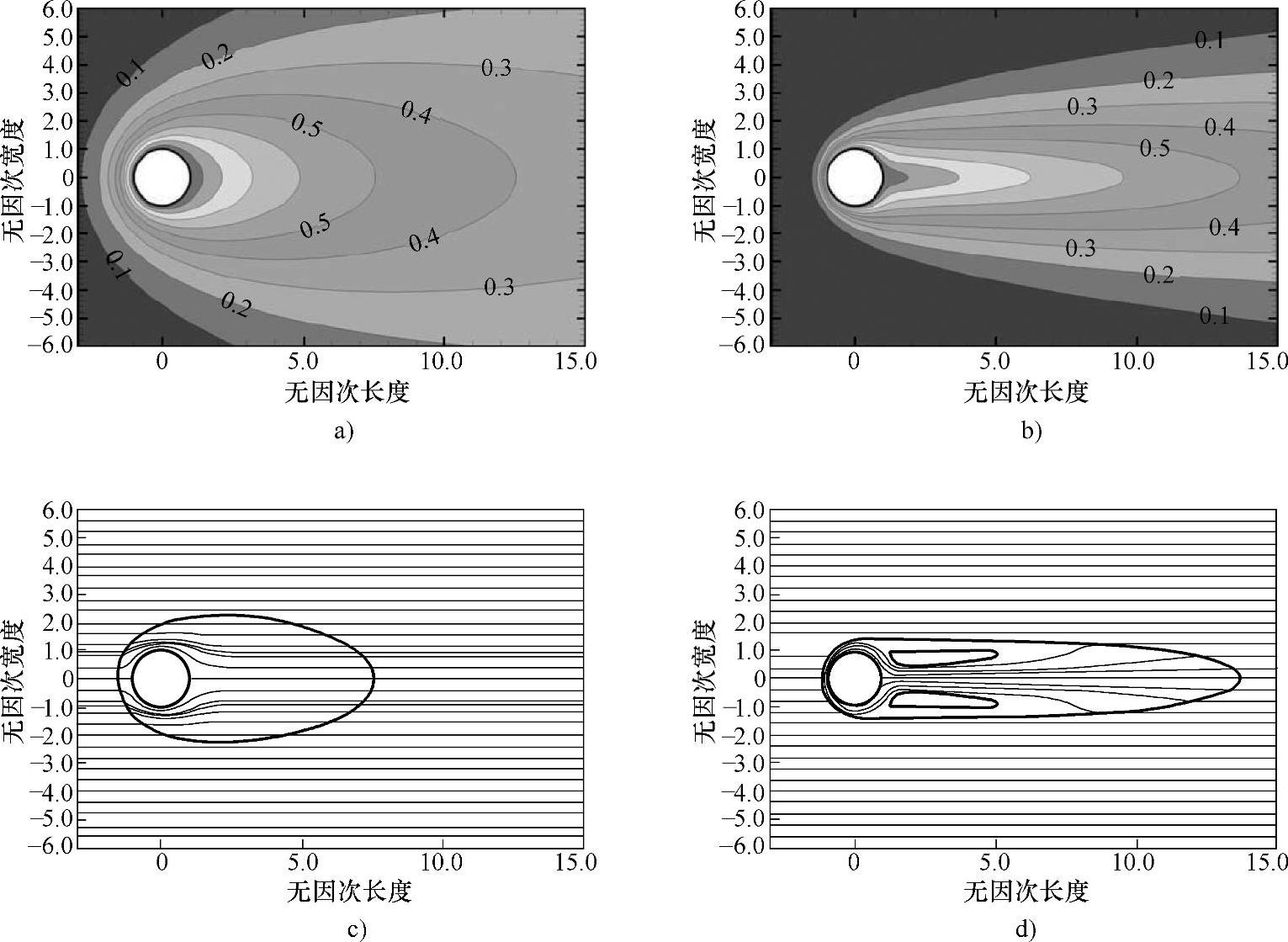
图1.5-28 Θ_m=0.5和Pr=0.1情况下计算的无因次温度场和速度场

a）、c）Pe=1 b）、d）Pe=4

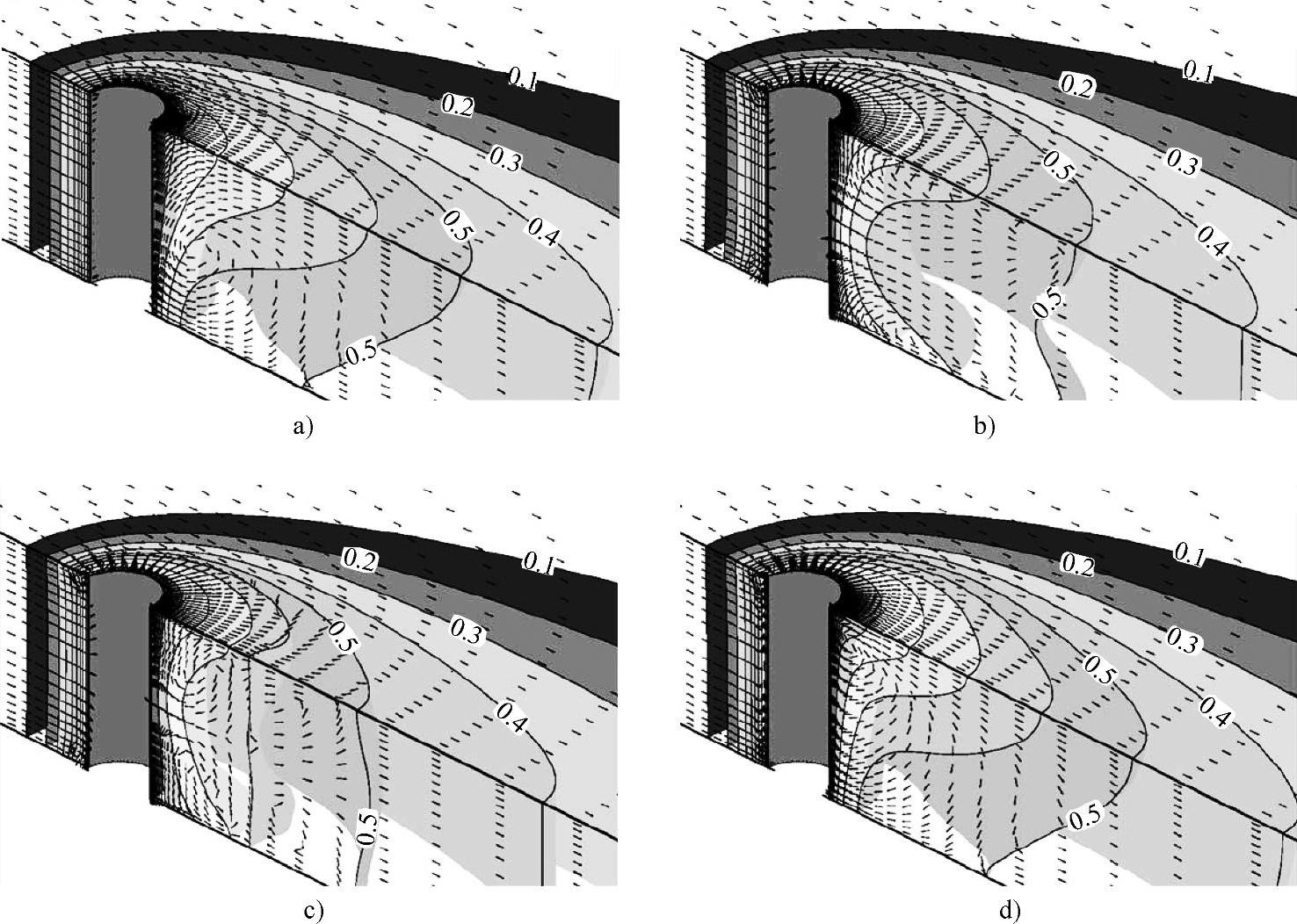
图1.5-29 在Pe=0.1、Pr=0.1、Θ_m=0.5、Z_max=5.0条件下，改变其他参数计算的温度场和速度场分布

a）浮力的影响：Gr=1000、Ma=W_key=0 b）表面张力的影响：a=0.000、Ma=1000、Gr=W_key=0 c）表面张力的影响：a=0.004、Ma=1000、Gr=W_key=0 d）摩擦力的影响：W_key=10、Gr=Ma=0

3.脉冲TIG焊电弧温度场的数值模拟

（1）计算模型的建立 采用直流正极性接法，电极直径为3.2mm。基本假设如下：

1）纯氩气氛条件下的电弧处于热力学平衡态。

2）电弧是轴对称的，流体流动为层流。

3）黏度耗散忽略不计。

4）电流波形为理想的直流方波脉冲。

在此假设条件下，可得计算的控制方程与边界条件。

连续方程：

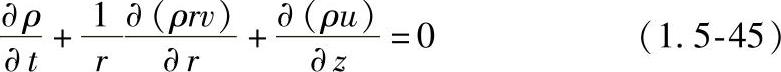
径向动量守恒方程：

y方向动量守恒方程：

能量守恒方程：

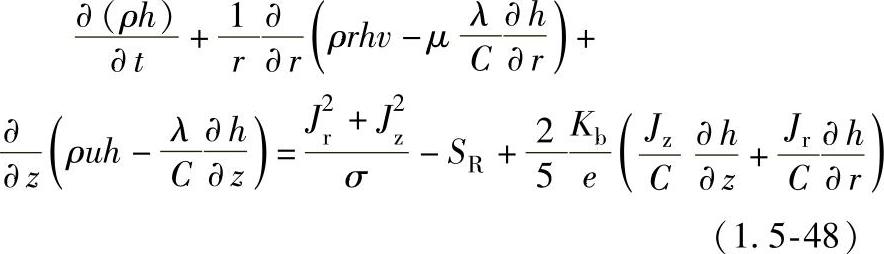
焓定义为

动量方程的电磁力和能量方程焦耳热的计算需要知道电流密度J和磁感应强度B。这需要求解电磁场的麦克斯韦方程组。

欧姆定律：

轴对称条件下，电流连续方程可表示为：

磁场强度由安培定律计算：

计算区域如图1.5-30所示。

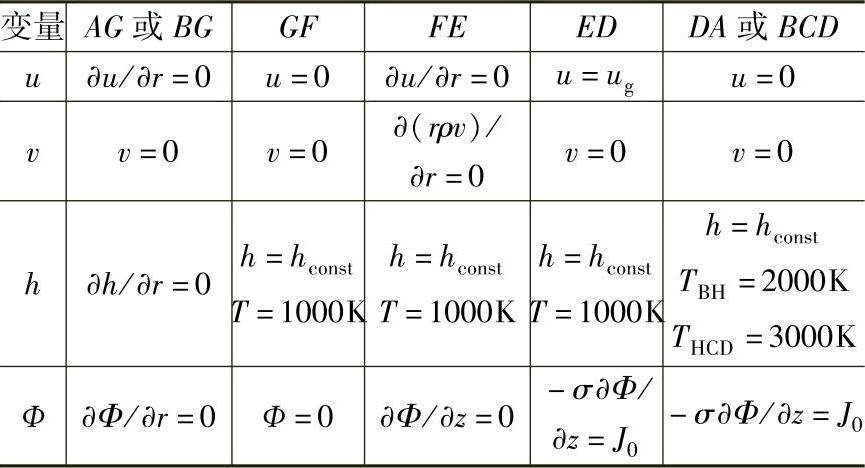
计算选取的边界条件见表1.5-5。

图1.5-30 脉冲焊接电弧计算区域

表1.5-5 计算选取的边界条件

在DE边界，径向速度为零，轴向速度分量按管道流方程确定，即：

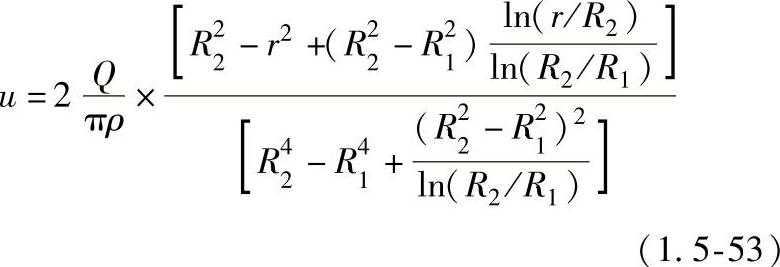
式中 Q——保护气体流量；

R₁——电极半径；

R₂——保护嘴的内半径。

计算模型的网格剖分如图1.5-31所示，阴极和阳极表面网格布局较密，以更好地计算独立变量的快速变化。

（2）数值计算 采用适体坐标变换法将物理平面（r，z）的控制方程转换为计算平面（ξ，ζ）的控制方程，而后进行离散求解。为此，将控制方程用统一控制方程来表示：

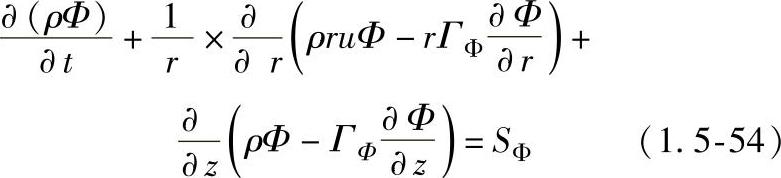
式中 Φ——通用变量，取不同的量时，表示不同的方程：Φ=1时为连续性方程，Φ=u和v时分别为径向和轴向的动量方程，Φ=h时为能量方程（焓的形式）。

Γ_Φ和S_Φ——与不同方程对应的广义扩散系数和广义源项。

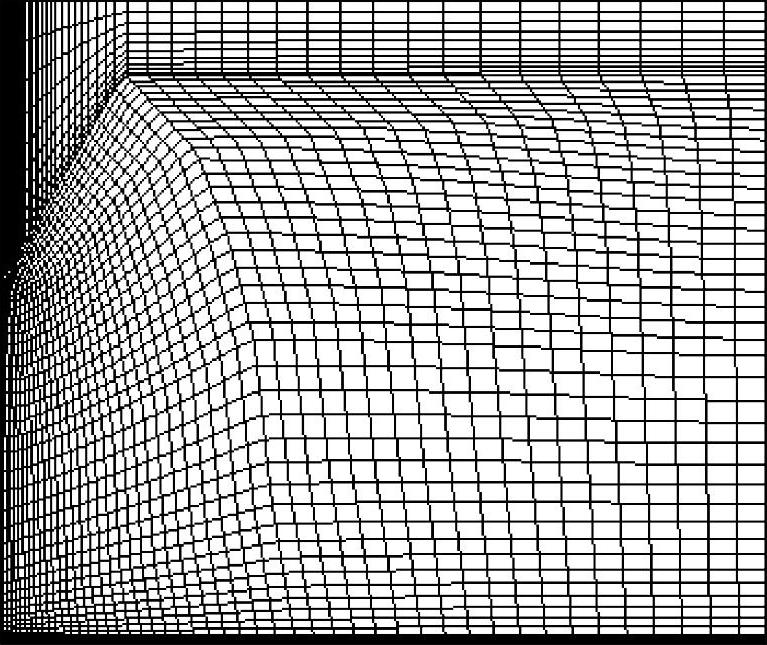
图1.5-31 计算模型的网格剖分

式（1.5-54）的转换形式如下：

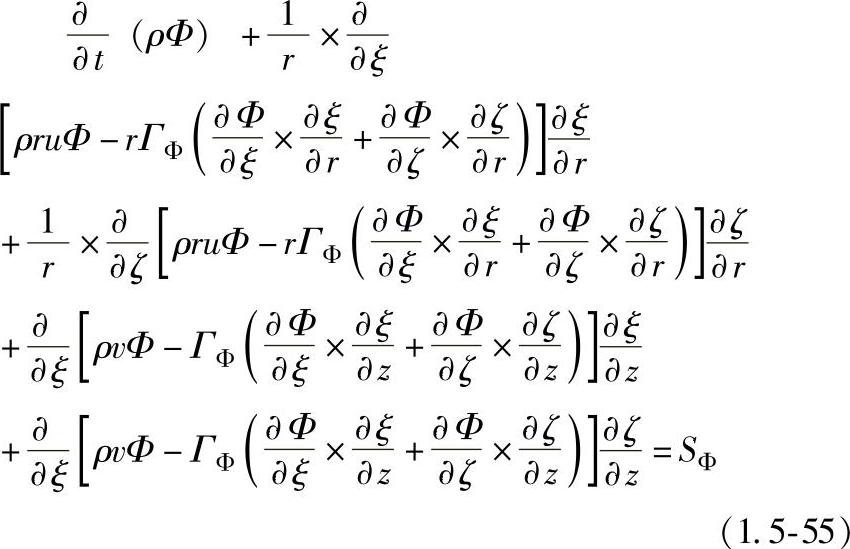
式中：

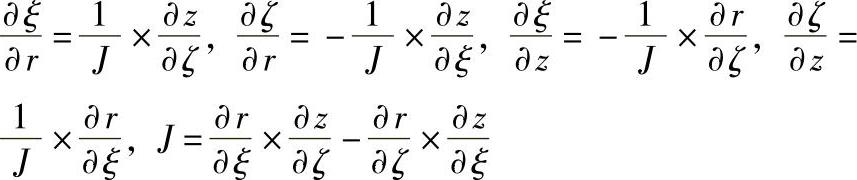
为简化转换系数的计算，计算平面的网格尺寸（Δξ，Δζ）取单位长度。

（3）计算结果 图1.5-32所示为计算所得低频脉冲TIG焊电弧的温度分布。图1.5-33所示为计算和实验所得不同脉冲电流条件下，阴极表面电弧压力的变化。图1.5-34所示为10000K等温线在电流突变过程中的变化。

4.TIG焊接电弧与熔池系统的双向耦合数值模拟

以TIG定点焊接电弧与熔池作为研究整体，建立电弧-熔池系统的统一数学模型，通过动态交互边界条件的不断更新，实现电弧-熔池系统双向耦合求解。

（1）基本假设 基本模型如图1.5-35所示。

1）对于焊接电弧的主要假设如下：

图1.5-32 计算所得低频脉冲TIG焊电弧的温度分布

I_p=100A I_b=25A 弧长L=2mm f=1Hz δ=0.5 θ=60°

①电弧是轴对称的，且处于层流状态。

②电弧等离子体处于局部热平衡状态。

③等离子体具有光学薄层特性，即辐射的重新吸收和总辐射相比可忽略不计。

④浮力和黏性热耗散忽略不计。

2）对于焊接熔池的主要假设如下：

①流体流动和传热是轴对称的，熔池内的流体为不可压层流体。

②除表面张力温度系数、比热容和热导率外，其余热物理常数与温度无关。Boussinesq假设成立。

③电弧压力只与熔池表面的下凹有关。

（2）控制方程 根据以上假设，在圆柱坐标下，用以描述TIG焊接电弧-熔池系统的统一模型控制方程组通用形式为：

式中的广义扩散系数Γ_Φ和广义源项和S_Φ具体表达式见表1.5-6和表1.5-7。

（3）电磁力、电弧控制方程的焦耳热和电子运动引起的能量输送项 电弧和熔池控制方程中的电磁力是以-J_zB_θ和J_rB_θ的形式分别加入到径向和轴向动量方程中的，电弧能量控制方程中焦耳热和电子运动引起的能量输送项也包含了J_z和J_r，因此需要求解相应的电磁场方程。

电流连续方程：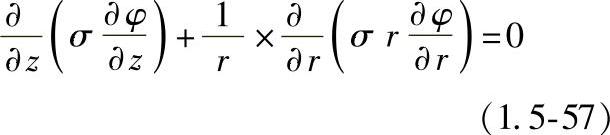

欧姆定律：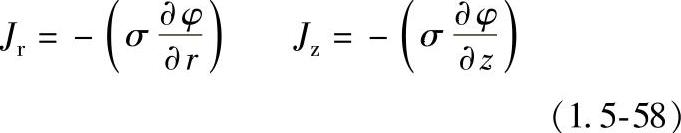

安培定律：

图1.5-33计算和实验所得不同脉冲电流条件下，阴极表面电弧压力的变化

a）计算值b）实验值

图1.5-34 脉冲电弧10000K等温温线的变化

a）I_p到I_b变化 b）I_b到I_p变化

I_p=100AI_b=25AL=2mmf=1Hzδ=0.5 θ=60°

（4）糊状区内流体流动 液/固混合区的流体流动按多孔介质处理，在径向和轴向动量方程中分别引入一个与温度有关的Darcy项-Ku、-Kv。渗透率K按下式计算：

在液相区，K=0，动量方程中的速度即为实际流速；在固相区，K→∞，动量方程中的瞬态项、对流项、扩散项相对于Darcy阻力项其值很小，整个方程由Darcy项控制，迫使速度趋于零。在糊状区，Darcy项的作用取决于液相体积分数的大小，因此速度随液相体积分数变化。

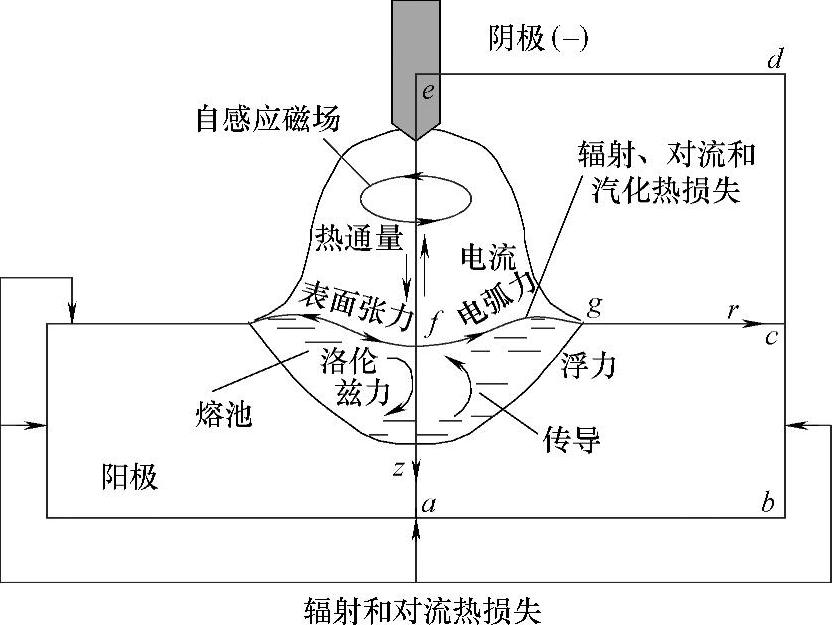
图1.5-35 TIG焊接示意图

注：abcdefa为计算区域

表1.5-6 TIG焊接电弧控制方程中的广义扩散系数和广义源项

表1.5-7 熔池熔化过程控制方程中的广义扩散系数和广义源项

（5）液相分数 在计算焊接熔池的能量方程中，源项中液相体积分数f_l按式（1.5-61）计算：

（6）表面张力 在熔池加热表面上，表面张力沿表面的变化与流体内的剪切应力相平衡：

表面张力γ与温度T和表面活性元素活度之间的关系按式（1.5-63）计算：

γ=γ_m-A_γ（T-T_m）-RTΓ_sln[1+K_sega_i] （1.5-63）

其中：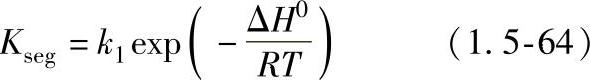

液态金属表面张力温度系数可通过式（1.5-63）对温度求导获得：

在稀释的液态Fe基合金中，Cr和Ni对硫（S）活度系数f_S的影响可用相互作用系数来表示。

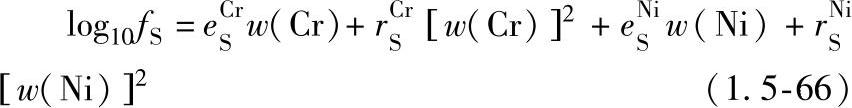
AISI 304不锈钢中Cr和Ni与S的一阶和二阶相互作用系数分别为

如果仅考虑表面活性元素（S）的作用，则方程（1.5-66）中S的活度和活度的导数可表示为

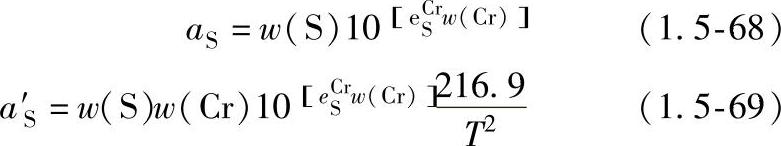
（7）熔池表面变形 焊接熔池的上表面在电弧压力、重力和表面张力作用下达到动态平衡。表面形状可用力平衡方程确定：

式中，。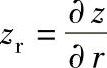

在计算过程中，非线性微分方程式（1.5-70）的差分格式用迭代法求解。通过不断更新拉格朗日乘子λ_L以使计算结果满足这一约束方程。

（8）边界条件 由于模型的对称性，计算区域取整个模型的一半。在熔池与电弧的中心线上按对称边界条件计算；在计算试样的加热表面、侧表面和底表面上的热损失为

q_loss=hc（T-T_a） （1.5-71）

式中，h_c按式（1.5-72）计算。

h_c=24.1×10^-4εT^1.61 （1.5-72）

（9）数值求解 研究采用适体坐标变换法将物理平面（r，z）的控制方程转换为计算平面（ξ，ζ）的控制方程，而后进行离散求解。

转换形式的统一模型方程组用控制容积积分法进行有限差分离散。扩散项用二阶中心差分离散，对流项用混合格式离散。在每一时间步长内，首先根据熔池自由表面形状，对电弧模型的求解区域和试样模型的求解区域进行网格剖分。而后求解电弧的控制方程组，计算电弧子系统的电流密度场、电磁力、温度场和流场，进而计算试样加热表面的电弧压力、热流密度、电流密度和电弧拖拽力，并将此作为熔池计算的输入条件，转入焊接试样控制方程组的求解，计算电流密度场、电磁力、温度场、确定熔池形状、计算熔池内的流体流动等，再迭代求解更新熔池自由表面形状，确定新的电弧计算区域和熔池计算区域形状，如此反复，直至电弧-熔池系统的循环迭代求解满足自由表面力的约束方程和控制方程变量的迭代收敛条件后，进入下一时间步长的计算。

焊接熔池固/液边界的确定采用了以下求解步骤，即焊接试样温度场和流场的计算采用了两套网格体系。首先根据温度场的计算结果，插值确定固液边界，再对熔池区进行网格剖分，并将温度场的计算结果插值到熔池计算区域网格结点上，而后求解动量方程以获得熔池内的速度场。

在数值计算中相互耦合的u、v、h、p代数方程组分两层迭代求解。外层为不同变量方程组系数的耦合迭代，内层是同一变量方程组的迭代求解。在外层迭代中，要对各变量离散方程的源项和系数用求解的变量之值不断更新。内层迭代采用ADI线扫描+双块修正。速度压力耦合采用SIMPLE算法。收敛判据为

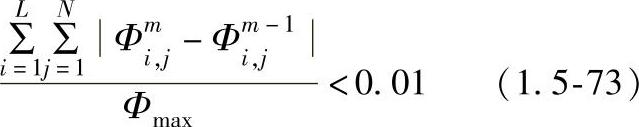
式中 L、N——r、z方向的结点总数；

m——迭代次数。

（10）计算结果 由于AISI304不锈钢材料具有较完整的热物理参数，并且有较多的计算分析和试验结果，所以以AISI304不锈钢为研究对象，氩气作为保护气体。计算选用的焊接参数：弧长5mm，焊接电流200A，电弧电压18V，电极锥角60°，电极直径3.2mm，电极尖角半径0.2mm，保护气体流量10.0L/min，试样半径10mm，试样厚度7.0mm，计算材料硫含量0.003%（质量分数）。

图1.5-36为不同加热时刻电弧温度场、熔池内流场和熔池形状计算结果。

5.脉冲GTAW熔池行为和焊缝成形的三维数值模拟

用建立的三维非稳态数值模型，研究脉冲电流钨极气体保护电弧焊（GTAW）的熔池输运现象及其对焊缝成形的影响。模拟熔池内瞬态速度和温度分布、熔池形态变化以及焊缝形状，分析脉冲电流频率对焊波的影响。

（1）控制方程 图1.5-37为GTAW平板堆焊过程的示意图。假定电弧热和电弧压力呈高斯分布，据此建立如下的非稳态控制方程组。连续性方程：

动量方程：

能量方程：

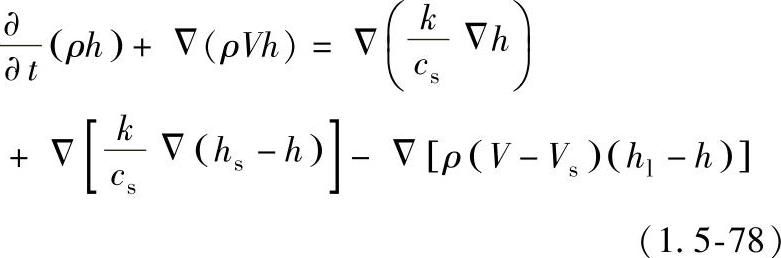
式（1.5-74）～式（1.5-78）中的符号说明如下：

p——压力；

u、v、w——x、y、z方向的速度；

V——速度矢量；

J——电流密度矢量；

B——磁感应强度；

β_T——表面传热系数；

T——温度；

ρ——材料的密度；

μ_l——黏性系数；

c——比热容；

k——热导率；

K——渗透函数；

h——比焓；

C——惯性系数；

f_s、f_l——固、液态体积分数；

g——重力加速度；

V_r——两相区内液相与固相的相对速度矢量，V_r=V_l-V_s；

下标s和l分别表示固态和液态。

图1.5-36 计算所得不同加热时刻焊接电弧温度场和熔池形状与尺寸

a）加热0.5s b）加热1.0s c）加热1.5s d）加热2.0s

（2）自由表面的跟踪 利用流体体积（VOF）法跟踪自由运动表面，该方法引入流体体积分数F（x，y，z，t）表示单位容积内流体所占的比例，满足以下方程：

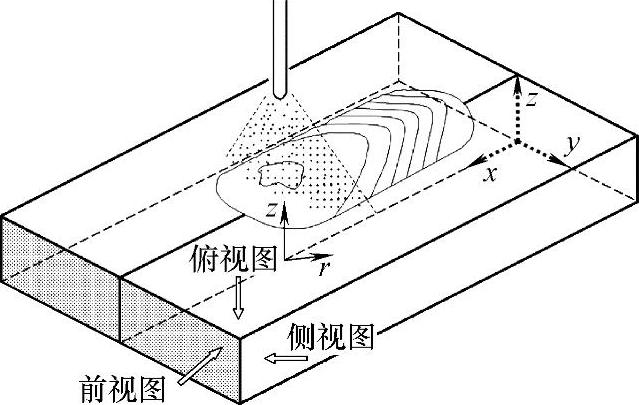
图1.5-37 GTAW平板堆焊过程的示意图

若F=1，对应的单元格内充满金属；若F=0，单元格内没有金属；而当F为0～1之间时，则表示金属的自由表面位于该单元格内。这样，可利用F计算自由表面单元及其法线方向，确定熔池的自由表面轮廓。

（3）边界条件

1）沿自由表面垂直方向上的压力p应满足：

p=p_arc+γκ （1.5-80）

式中 p_arc——电弧压力，；

κ——自由表面的曲率。

2）自由表面切线方向上，温度相关的Marangoni切应力表示为

式中s——正切于自由表面的矢量。

3）在焊件顶部，假设热流方向均垂直于焊件表面。因此焊件顶部的温度边界条件为

式中 I——电流；

η——电弧传热效率；

u_w——电弧压力；

σ_q——电弧热流分布参数。

由对流、辐射和蒸发产生的热损失为

式中 H_ev——液-气相变的汽化热；

W——熔化金属的蒸发率。

4）对称面y=0

5）其他表面

式中 n为x、y或z方向。

（4）电磁力 假定电场为准静态及电导率为常数，电流方向指向负z方向，电势φ满足麦克斯韦方程：

在焊件的上表面满足以下条件：

式中 σ_e——电导率；

σ_c——电流分布参数。

获得电势的分布之后，r-z方向上的电流密度J_r、Jz和自感应角向磁感应强度B_θ可由式（1.5-88）和式（1.5-89）计算：

式中 μ₀——磁导率。

电磁力三个方向上的分量由式（1.5-90）计算：

（5）数值方法 对控制方程及边界条件进行迭代计算。在每一时间步长内进行如下动作：

1）更新参数计算电流连续性方程，获得该时刻的电流和电磁力分布。

2）更新自由表面上的作用力以及热流强度分布，计算动量和能量方程。

3）解VOF方程，获得新的金属自由表面形状，更新计算区域各单元内的物性参数和边界条件。

4）更新时间并将电弧中心移至新的位置，返回至步骤1）重复上述过程，直至计算结束。

计算区域的尺寸为x×y×z=300mm×30mm×10mm。由于计算区域沿x-z平面对称，实际中仅计算一半区域，网格点为610×76×82（x×y×z）。熔池沿焊接方向移动，计算中使用了自适应的非均匀网格，熔池附近具有更密的网格。计算中平均时间步长为10^-4s。

（6）计算结果 计算以304L不锈钢平板（长300mm、宽30mm、厚6mm）为对象，钨极焊丝连同电弧沿x轴正方向匀速移动。连续电流为130A，电压为12.2V；脉冲电流的峰值电流为200A（电压12.5V），基值电流为42A（电压11.2V），脉冲频率包括4个等级（分别为1Hz、2Hz、5Hz、10Hz），占空比为0.55；焊接速度为0.34cm/s。

为避免可能的末端影响，焊接从x=10.0mm处开始；此时，时间设为t=0s。

图1.5-38为连续电流下，焊件内温度和速度的分布侧视图；图1.5-39为脉冲电流（f=1Hz）下，焊件内温度和速度分布的变化侧视图；图1.5-40所示为脉冲电流频率对焊波的影响；图1.5-41所示为脉冲GMAW凝固焊缝表面形状的计算结果和实验结果比较。

图1.5-38 连续电流下，焊件内温度和速度的分布侧视图

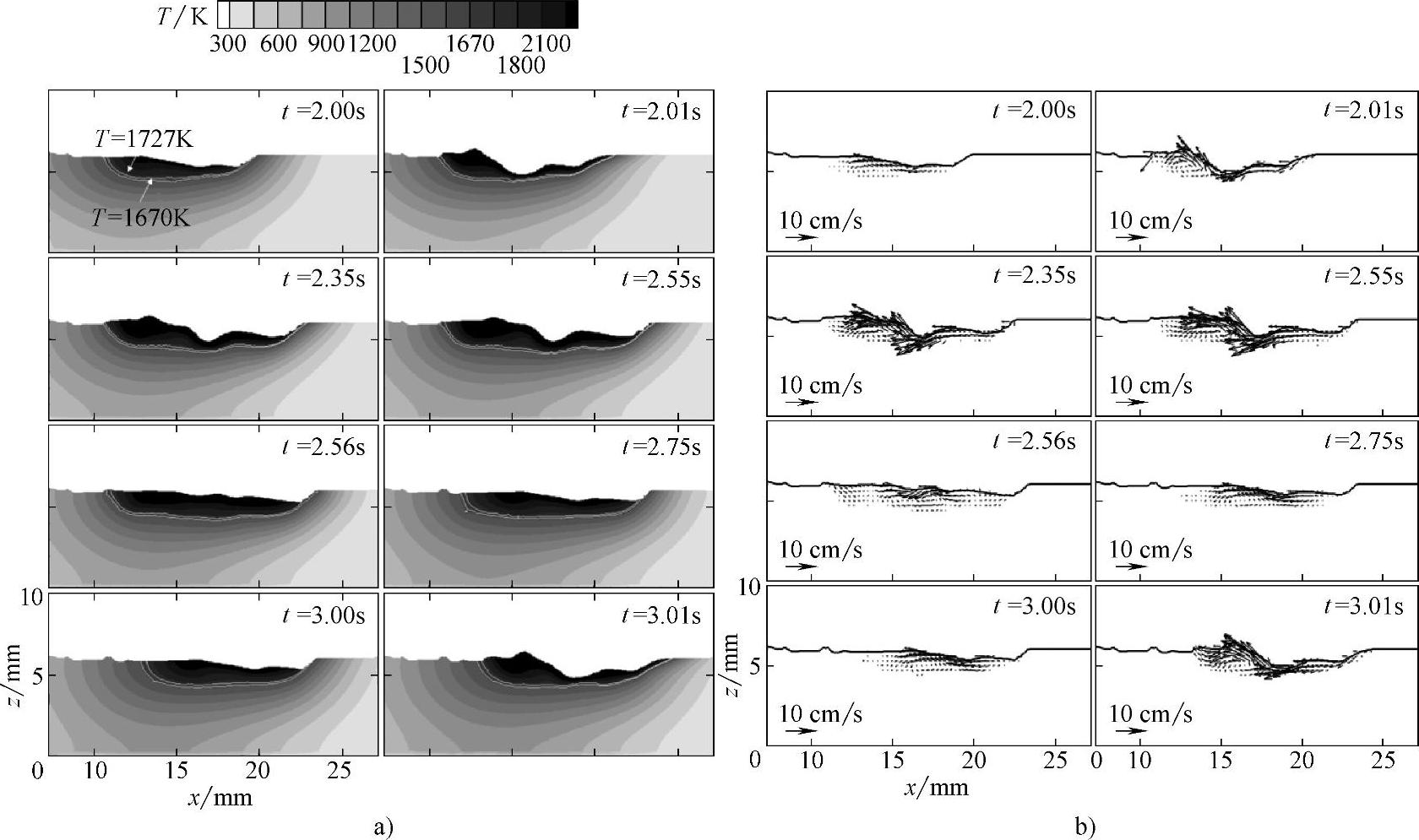
图1.5-39 脉冲电流（f=1Hz）下，焊件内温度和速度分布的变化侧视图

a）温度 b）速度

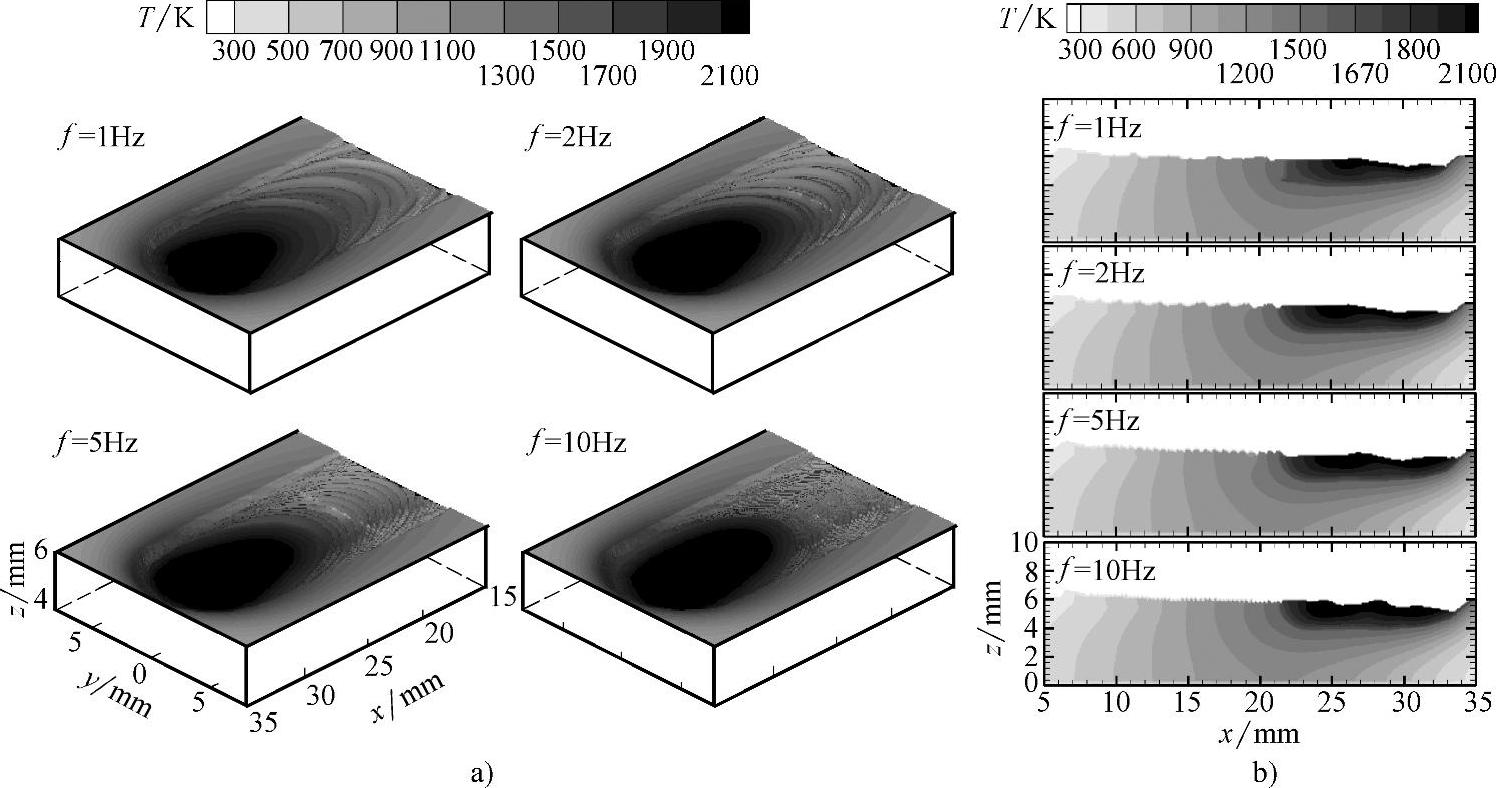
图1.5-40 脉冲电流频率对焊波的影响

a）三维焊缝形状及温度分布 b）温度分布侧视图

t=6.00s

图1.5-41 脉冲GMAW凝固焊缝表面形状的计算结果和实验结果比较

a）计算结果 b）实验结果