控制系统可以通过调整开环增益满足稳态性能指标要求,但相位裕量过小,不满足相对稳定性要求,需要采用超前校正环节进行校正。
1.相位超前校正原理及其频率特性
超前校正环节的等效RC电路如图5-30所示,其传递函数为
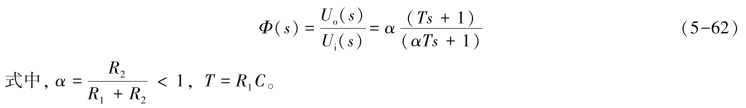
超前校正环节的幅频特性和相频特性分别为
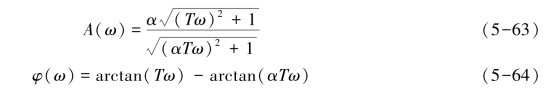
因α总小于1,则相位角φ(ω)总是大于0°,所以又把该校正器称为相位超前校正环节。
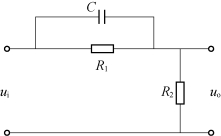
图5-30 超前校正环节的等效RC电路
为了直观表达超前校正环节的幅值特性和相频特性,现在假设式(5-62)中T=0.2,因α<1,α分别取0.2、0.5、0.8时,执行以下MATLAB程序,绘制相位超前校正环节的Bode图,如图5-31所示。MATLAB程序如下


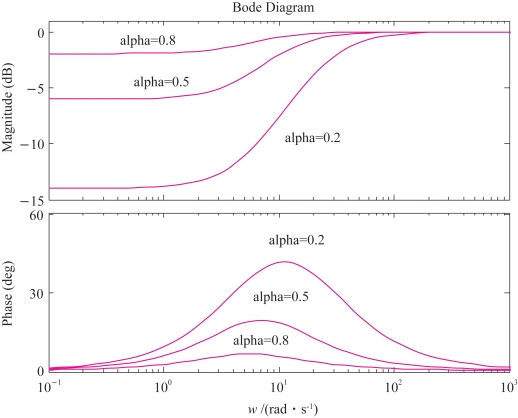
图5-31 超前校正环节的Bode图
2.采用Bode图进行相位超前校正
【例5-6】已知单位负反馈控制系统的开环传递函数为(https://www.xing528.com)
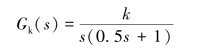
要求系统的稳态速度误差系数Kv=20 s-1,相位裕量γ≥50°,幅值裕量Kg≥10 dB,试设计系统的超前校正环节。
解 根据
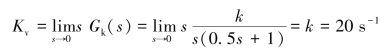
可求出k=20,即
![]()
因为H(s)=1,所以前向通道传递函数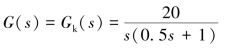
MATLAB程序如下

利用以上程序可绘制系统校正前后的Bode图,如图5-32所示。求得未校正系统的幅值裕量Gm1=1.785 2e+003,相位裕量Pm1=17.966 0°<γ,当α=0.237 5时,校正后系统满足设计要求,超前校正环节造成对数幅频特性在ωm=8.949 8 s-1点处的上移量am=10lg α=-6.242 9 dB,ωm就是校正后系统的剪切频率ωcp=8.949 7 s-1,对应的T=0.229 3 s,为了补偿超前校正造成的幅值衰减,原开环增益要加大K1倍,使K1α=1,故K1=1/0.237 5=4.21;校正后的幅值裕量Gm=439.418 7,即20×log10(439.418 7)=52.857 6 dB,相位裕量Pm=50.628 5°,已满足设计要求。
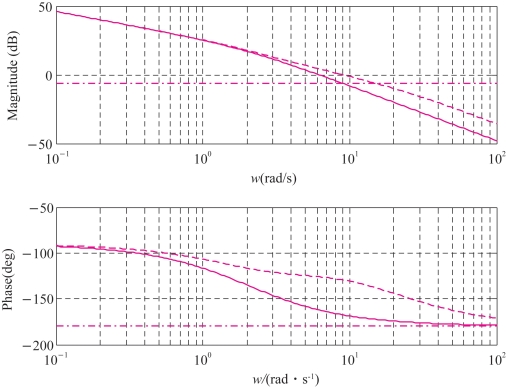
图5-32 校正前后系统的Bode图
相位超前校正环节的传递函数为
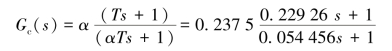
校正后,系统的传递函数为
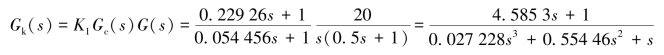
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




