PID控制器优化策略

从前面的讨论可以知道，PD控制器可以为系统提供阻尼，但稳态响应不受影响；PI控制器可以同时改善相对稳定性和稳态误差，但系统的上升时间要加大。PID控制器可同时利用PD和PI控制器的优点。PID控制器就是同时采用PD、PI控制器，综合二者的优点，其设计过程也可以分为PD设计和PI设计两个过程。PID控制器的设计过程大致如下。

（1）认为PID控制器由一个PI控制器和一个PD控制器串联而成，如图5-27所示。PID的传递函数可以做如下变形

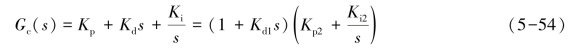
PID中有3个参数需要设计，因此把PD部分的比例环节设置为单位量1，式（5-54）中左右参数之间的关系如下

（2）设计PD校正器先考虑只有PD控制器的情况，选择Kd1使得满足相对稳定性要求。在时域，相对稳定性要求可以由最大超调量衡量；在频域，则可以由相位裕量衡量。如果单独使用PD校正器可满足系统的性能指标，则设计结束，否则考虑增加PI校正器。

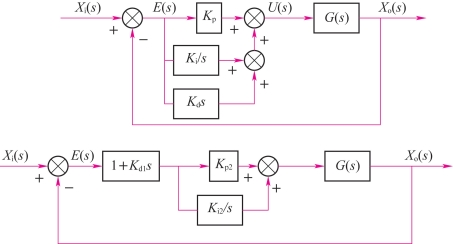
图5-27　PID控制器

（3）设计PI校正器，选择参数Ki2和Kp2，满足所有的相对稳定性要求。

作为一种选择，也可以先设计PI控制器来满足相对稳定性要求，然后，再设计PD控制器。下面的例子将说明如何设计PID控制器。

【例5-5】单位反馈系统（某飞机高度控制系统）的开环传递函数为

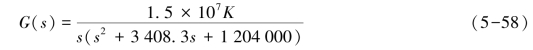
根据闭环系统的时域性能指标要求，设计系统的PID控制器。性能指标如下：

由输入信号产生的稳态误差＜0.000 43；

最大超调量＜5%；

上升时间＜0.005 s；

调整时间＜0.005 s。

解　PID控制器设计如下。

（1）为满足稳态误差要求，取K=181.17，此时最大超调量为78.88%。

（2）设计PID控制器的PD部分。当K=181.17，具有PD控制器时，参考式（5-54）系统的前向传递函数为

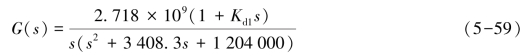
只要确定Kd1即完成了PD控制器的设计。

由于高阶系统很难用解析表达式来描述性能指标与传递函数系统之间的关系，因此需要借助设计工具如MATLAB来完成设计。表5-5给出了Kd1变化时，系统时域指标最大超调量MP、上升时间tr、调整时间ts，频域指标幅值裕量h、相位裕量γ、谐振峰值Mr。

表5-5　具有PD校正器的三阶系统的闭环性能指标

(www.xing528.com)

续表

因此，PD控制器对该三阶系统的校正效果如下：

①系统最大超调量的最小值为11.37%，此时Kd1大约为0.002；

②上升时间得到改善；

③Kd1太高会增加最大超调量，增加调整时间（因为阻尼比太小）。

表5-5中，Kd1=0对应没有校正器时的指标，即式（5-59）对应的指标。发现如果原系统具有非常低的阻尼或不稳定，则PD控制器在改善系统的稳定性方面效果不佳。PD控制器校正效果差的另外一种情况是被校正系统的相频特性曲线在幅值穿越频率附近太陡，由于（PD控制器所引发的）幅值穿越频率的增加，原相位裕量会快速减小，大大削弱PD控制器的校正效果。

从频域角度分析，由于PD控制器的使用，相频特性曲线始终在-180°轴上方，其相位穿越频率为无限大，因此幅值裕量变为无限大，此时相位裕量成为系统的主要相对稳定性指标。当Kd1=0.002时，相位裕量达到最大约为58.42°，同时Mr达到最小的1.07。当Kd1在0.002以上继续增加时相位裕量减小，这与时域得出过大的Kd1将会减小系统的阻尼的结论相一致。

（3）设计PID控制器的PI部分。

下一步，我们再加入PI控制器，前向传递函数变为

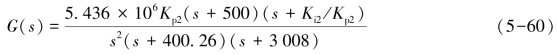
以尽量选择相对已有零-极点比较小的Ki2/Kp2为原则，取Ki2/Kp2=15，式（5-60）变为

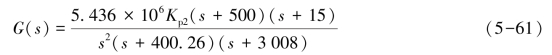
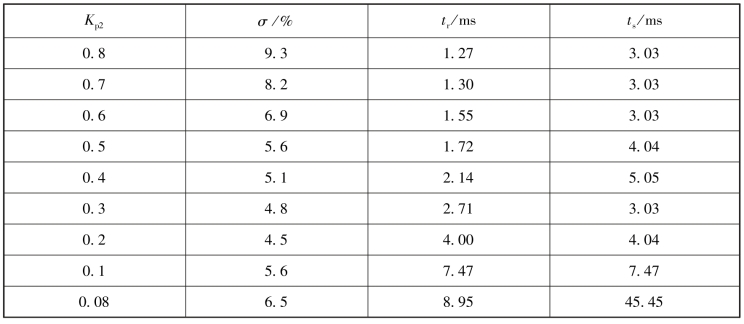
用与前面相同的方法得到表5-6，表中给出了在Ki2/Kp2=15前提下，Kp2变化时，式（5-61）对应的闭环系统的时域指标值。从表中发现最好的Kp2值应该在0.2到0.4之间。

表5-6　经PID校正的三阶系统的单位阶跃响应指标

续表

选择Kp2=0.3，Kd1=0.002，Ki2=4.5，利用式（5-55）～式（5-57）可以得到PID的参数

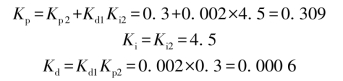
图5-28是本例中经过PID、PD控制器校正前后系统的单位阶跃响应的比较，图5-29是本例中经过PID、PD控制器校正前后系统的开环传递函数的Bode图比较。

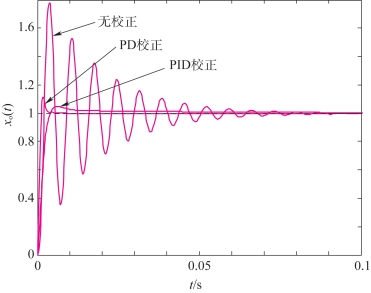
图5-28　PID、PD控制器校正前后阶跃响应比较

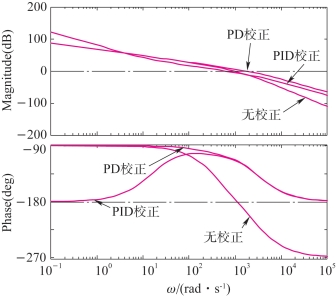
图5-29　PID、PD控制器校正前后Bode图比较