如何使用PD控制器？

1.PD控制器的特性

1）PD控制器的构成

图5-16所示为具有PD控制器的控制系统，假设被控对象为标准二阶系统，即有

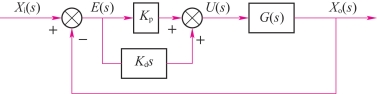
图5-16　具有PD控制器的控制系统

PD控制器的传递函数为

加到被控对象的控制信号为

式中，Kp、Kd分别是比例常数和微分常数。

图5-17所示为利用电路实现PD控制器，在图5-17（a）中，Kp、Kd分别为

图5-17（a）中电路简单一些，但Kp、Kd不能独立进行选择。

图5-17（b）中Kp、Kd分别为

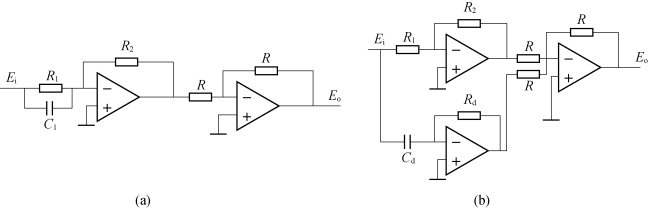
图5-17　运算放大器实现PD控制器的电路

图5-17（b）的电路比图5-17（a）的电路稍微复杂一点，但两个参数可以独立选择。关于如何来更好地设计电路来实现控制器，这里不做进一步讨论。

经过校正以后的系统开环传递函数为

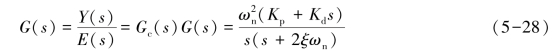
2）PD控制的时域解释

由于de（t）/dt反映的是e（t）的斜率，因而PD控制是一种预测控制，即通过计算e（t）的斜率，PD控制器可以预测误差的方向并利用它来改善控制过程。通常，就线性系统而言，单位阶跃响应的输出xo（t）或误差信号e（t）的斜率越大，系统的超调量也越大。微分控制测量到e（t）的即时斜率，提前预测到系统的过量超调，在此超调发生以前为系统提供合适的修正。

只有当系统的稳态误差随时间发生变化时，微分控制才会影响到系统的稳态误差。如果系统的稳态误差相对于时间是一个常数，微分控制为系统所提供的控制量为0。但如果稳态误差随着时间持续增加，微分控制则会向系统提供与de（t）/dt成正比的控制量，从而减小误差的幅值。

从式（5-28）可以看出，PD控制器不会影响到系统的型别，所以对于单位反馈系统而言，PD控制器不会影响到稳态误差。

3）PD控制器的频域解释

PD控制器的传递函数为

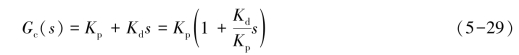
在频域设计PD控制器，很容易用Bode图来说明设计方法。图5-18所示为Kp=1时的PD控制器的Bode图。通常Kp可以和系统的某个前向增益结合，所以认为PD控制器的直流增益为单位增益并不影响对问题的讨论。从图5-18可以清楚地看出，PD控制器具有明显的高通滤波器特征，其相位超前的特征可以用来增加系统的相位裕量，但同时它的幅频特性提高了系统的穿越频率。设计PD控制器时，把它的角频率ω=Kp/Kd放到适当的位置，使得在新的幅频特性的穿越频率点，系统的相位裕量得到一定的提高。对于一个给定的系统，该Kp/Kd有一个取值范围可供选择，可用于调整系统的阻尼。另外一个要考虑的实际问题是Kp和Kd的值会影响到PD控制器的实现。PD控制器在频域中的另外一个明显的影响是由于高通特性，多数情况下会增加系统的频宽ωb，减少系统的上升时间。同样由于其高通特性，PD控制器会加强系统中来自输入的高频噪声干扰。

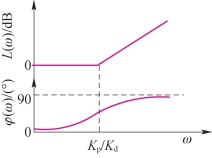
图5-18　PD控制器的Bode图

4）PD控制效果

适当设计PD控制器，可以解决系统不稳定或系统的稳定裕量太小的问题，另外，PD控制器可以从以下几个方面影响系统的性能：

（1）增加系统的阻尼、减少系统的超调量；

（2）减少上升时间和调整时间；

（3）增加带宽ωb；

（4）增加幅值裕量Kg、相位裕量γ、谐振峰值Mr；

（5）可能加强高频噪声。

电路实现PD控制时需要较大的电容，即PD控制器参数不合适将会导致实现困难。

【例5-3】飞机高度控制系统如图5-19所示，其前向传递函数如下

要求系统具有以下性能指标：

单位阶跃斜坡输入引起的稳态误差≤0.000 443；

最大超调量≤5%；(www.xing528.com)

上升时间≤0.005 s；

调整时间≤0.005 s。

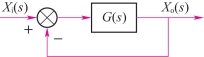
图5-19　飞机高度控制系统

解　在没有校正的情况下（或者说只有比例校正），为了满足给定的稳态误差要求，K至少为181.17，但在这种情况下，系统的阻尼比仅为0.2，最大超调量达52.7%。

现在考虑在系统的前向通道中用PD控制器对系统进行校正，改善系统的阻尼特性和超调特性，同时保持系统的单位阶跃响应误差不超过0.000 443。

2.PD控制器时域设计

对于例5-3，为满足误差不超过0.000 443，需要K=181.17。此时，包含PD控制器在内的系统的前向传递函数（即系统开环传递函数）为

系统的闭环传递函数为

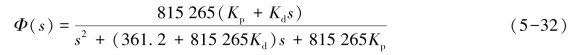
系统的速度系数为

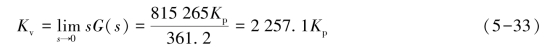
由单位斜坡输入引起的稳态误差为

从式（5-32）中发现PD控制器的效果如下：

（1）使得闭环传递函数增加了一个零点-Kp/Kd；

（2）闭环传递函数的阻尼项有所增加。即闭环传递函数的s项的系数由原来的361.2增加到361.2+815.265Kd。

特征方程如下

根据稳态误差要求，取Kp=1，这时，系统的阻尼比为

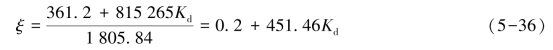
此式明显地说明了Kd为系统提供阻尼的效果。可以根据式（5-36）来设计满足闭环系统阻尼比的Kd。比如，Kd=0.001 1时，阻尼比为0.7，Kd=0.001 77时，阻尼比为1。

从式（5-32）可以看出，PD控制器的引入使得系统的开环传递函数多了一个零点-Kp/Kd，对此二阶系统而言，在Kd从0开始逐渐变大的过程中，该零点逐渐向坐标原点靠拢，对系统原有的极点s=0有越来越强的抵消作用，而系统的开环传递函数也越来越接近一个惯性环节，该惯性环节的极点就是s=-361.2。

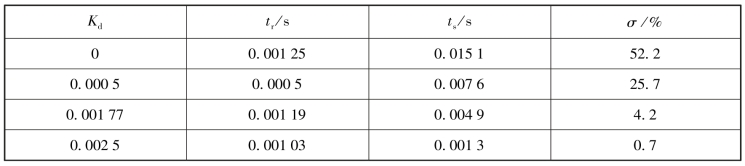
图5-20所示为例5-3的PD控制器的校正效果，包括没有PD控制和有PD控制器（Kp=1，Kd=0.001 77），几个参数的值可以利用时域计算方法通过MATLAB计算得到。有PD控制器时，系统的超调量为4.2%，虽然以临界阻尼条件选择了Kd，但由于闭环零点-Kp/Kd的影响，系统仍然有超调。表5-1列出的是当Kp=1，Kd取不同的几个值时闭环系统的上升时间、调整时间和最大超调量。从表5-1可以看出，当Kd≥0.001 77以后，表中的各项指标都可以满足要求。需要提醒的是Kd只要满足系统要求即可，因为Kd过大不仅会导致高频干扰，在实现PD控制器时也会遇到困难。

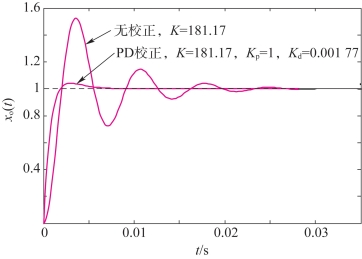
图5-20　例5-3的PD控制器的校正效果

表5-1　例5-3的具有PD校正器的单位阶跃响应主要指标

总之，PD控制器减少了最大超调量、上升时间和调整时间。

3.PD控制器频域设计

现在开始频域设计的讨论。不同的PD控制器的校正频域效果如图5-21所示，图中Kp=1，当Kd=0时，即为无PD校正时G（s）的Bode图，这种情况下，相位裕量为22.8°，谐振峰值Mr为2.522，系统处于欠阻尼状态。现给定性能指标如下：

单位阶跃斜坡输入引起的稳态误差≤0.004 43；

相位裕量≥80°；

谐振峰值Mr≤1.05；

频宽bω≤2 000 rad/s。

首先令Kp=1，然后确定参数Kd。因为只有一个参数Kd需要设计，因此可以使用非常简单的列表方法设计。具体做法：给出Kd的不同值，利用计算机软件计算出需要关心的指标参数，作成表格，根据表格选择合适的参数Kd。这种设计方法简单、容易操作，非常适合工程实际中高阶系统的设计。

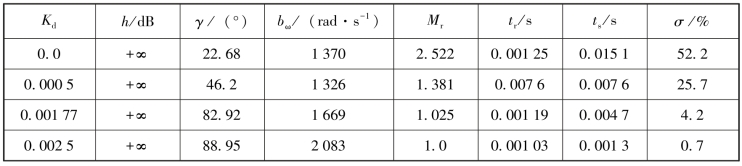
图5-21包含了Kp=1，Kd=0、0.000 5、0.001 77和0.002 5时G（s）的Bode图，经过这几个不同参数的PD控制器校正以后的系统的频域指标列在表5-2中，之所以用这几个参数是为了和时域的设计结果比较。这些Bode图和指标参数可以非常容易利用MATLAB设计工具得到，具体方法在其他的章节中有说明。

从图5-21发现，未校正（Kd=0）时系统幅值裕量始终为无穷，因此相对稳定性用相位裕量来衡量。当Kd=0.001 77时（对应于临界阻尼情况），相位裕量为82.93°，谐振峰值为1.025，频宽为1 669 rad/s，频域所要求的所有性能指标都可以达到。PD控制器还使得系统的穿越频率和带宽增大，相位穿越频率变得无穷大（-180°）。

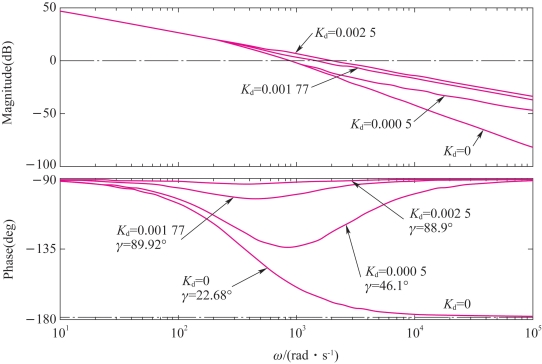
图5-21　不同的PD控制器的校正频域效果（Kp=1）

表5-2　例5-3中PD控制器在频域的校正效果（Kp=1）