相位滞后校正方法优化

1.相位滞后校正装置的特性

图5-6所示为RC相位滞后校正网络，其传递函数为

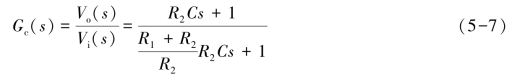
设

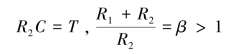
则

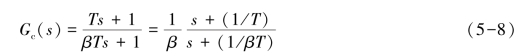
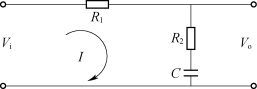
图5-6　相位滞后校正网络

相位滞后校正网络的Bode图如图5-7所示，由于传递函数式（5-8）中βT＞T，故对数幅频渐近曲线具有负斜率段，相频曲线出现负相移。负相移表明当正弦信号输入时，稳态输出电压在相位上滞后于输入，故称相位滞后校正网络。相位滞后校正网络的幅频特性为

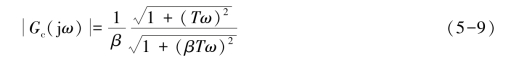
相频特性为

相位滞后校正网络的最大滞后角度φm及其对应的频率ωm为

由图5-7可以看出，相位滞后校正环节是一个低通滤波器。相位滞后校正的作用主要是利用它的负斜率段，使被校正系统高频段幅值衰减，幅值交界频率左移，从而获得充分的相位裕量，其相位滞后特性在校正中作用并不重要。因此，相位滞后校正环节的转折频率1/（βT）和1/T均应设置在远离幅值交界频率、靠近低频段的地方。

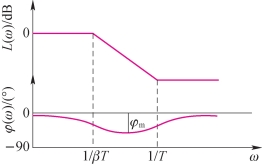
图5-7　相位滞后校正网络的Bode图

2.基于频率响应法的相位滞后校正

相位滞后校正的主要作用是在高频段造成衰减，从而使系统获得足够的相位裕量，相位滞后特性在滞后校正中不重要。

用频率响应法为图5-5所示的系统设计相位滞后校正装置的步骤如下：

（1）假设有下列相位滞后校正装置(www.xing528.com)

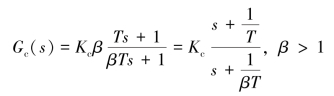
定义

于是

已校正系统的开环传递函数为

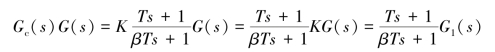
式中，G1（s）=KG（s）

确定增益K，使系统满足给定静态误差常数的要求。

（2）如果经过增益调整的未校正系统G1（jω）=KG（jω）不满足有关相位裕量和增益裕量的性能指标，则应寻找一个频率点，在这一点上，开环传递函数的相位等于-180°加要求的相位裕量。要求的相位裕量等于指定的相位裕量加5°～12°（增加5°～12°是为了补偿相位滞后校正装置的相位滞后）。选择此频率作为新增益交界频率。

（3）为了防止由相位滞后校正装置造成的相位滞后的有害影响，相位滞后校正装置的极点和零点必须配置得明显低于新增益交界频率，因此选择转角频率ω=1/T（相应于相位滞后校正装置的零点）低于新的增益交界频率一倍频程到十倍频程（如果相位滞后校正装置的时间常数不会很大，则转角频率ω=1/T可以选择在新的增益交界频率之下十倍频程处）。把校正装置的极点和零点选择得足够小，相位滞后就发生在低频范围内，从而将不会影响到相位裕量。

（4）确定使幅值曲线在新的增益交界频率处下降到0 dB所必需的衰减量。这一衰减量等于-20lg β，从而可以确定β值。另一个转角频率（相应于相位滞后校正装置的极点）可以由ω=1/（βT）确定。

（5）利用（1）、（4）中确定的K和β值，根据下式计算常数Kc

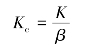
【例5-2】设单位负反馈系统原有的开环Bode图如图5-8中曲线L1、φ1所示，试分析其稳定性，并提出校正措施。

解　由图5-8可见，在中频段截止频率ωc1附近为-60 dB/dec，故系统动态响应的平稳性很差或不稳定，对照相频曲线可知，系统接近于临界情况。

将系统串联接入相位滞后校正环节，并将相位滞后校正环节的转折频率T-1、（βT）-1设置在远离ωc1的地方，这时校正后系统的开环对数频率特性如图5-8中曲线L2、φ2所示。由于校正环节的相位滞后主要发生在低频段，故对中频段的相频特性曲线几乎无影响。因此校正的作用，是利用了网络的高频衰减特性，减小系统的截止频率，由图5-8中的ωc1变为ωc2，从而使稳定裕量增大，保证了稳定性和改善振荡性。因此可以认为，相位滞后校正是以牺牲快速性来换取稳定性和改善振荡性的，同时由于校正后系统高频段衰减了因而校正后的系统具有较好的抑制高频干扰的能力。

图5-8中的曲线L1所对应的开环增益是根据稳态精度的要求而设计的，故由校正后的曲线L2可知，校正后系统既满足了稳态精度的要求又满足了稳定性振荡性的要求，较好地解决了这一对矛盾。

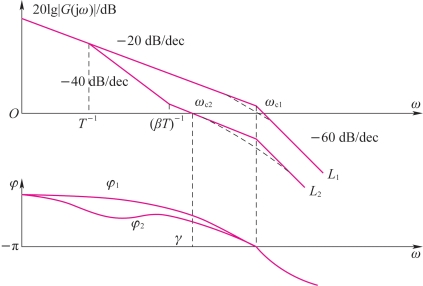
图5-8　例5-2的Bode图

综上，当控制系统具有良好的动态性能，而稳态误差较大时，低频段采用相位滞后校正可既保持原有的动态性能，又可使系统的开环增益大幅增加，以满足精度要求，但会减小截止频率，使响应时间增加。