如何确定最小相位系统的传递函数结构形式？

【例4-11】图4-55所示为由频率响应法获得的某最小相位系统的对数幅频曲线和对数幅频渐近特性曲线，试确定系统传递函数。

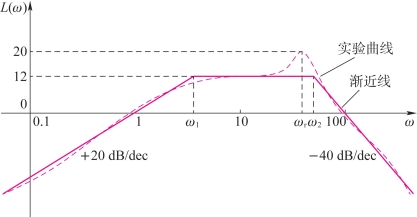
图4-55　对数幅频曲线和对数幅频渐近特性曲线

解　（1）确定系统积分或微分环节的个数。因为对数幅频渐近特性曲线的低频渐近线的斜率为-20ν dB/dec，而由图4-55知低频渐近线斜率为+20 dB/dec，故有ν=-1，系统含有一个微分环节。

（2）确定系统传递函数结构形式。由于对数幅频渐近特性曲线为分段折线，其各转折点对应的频率为所含一阶环节或二阶环节的交接频率，每个交接频率处斜率的变化取决于环节的种类，本例中共有两个交接频率：ω=ω1处，斜率变化-20 dB/dec，对应惯性环节；ω=ω2处，斜率变化-40 dB/dec，可以对应振荡环节，也可以为两个惯性环节，本例中，对数幅频特性在ω2附近存在谐振现象，故应为振荡环节。

因此所测系统应具有下述传递函数

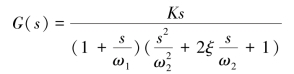
其中参数ω1，ω2，ξ及K待定。

（3）由给定条件确定传递函数参数。根据低频渐近线列方程为

得

由给定点（ω，La（ω））=（1，0）及ν=-1得K=1。

根据低频段直线列方程

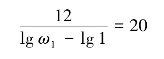(www.xing528.com)

根据高频段直线列方程

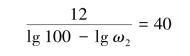
得

由前文知，在谐振频率ωr处，振荡环节的谐振峰值为

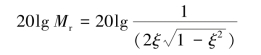
而根据叠加性质，本例中20lg Mr=20-12=8 dB，故有

解此方程，得ξ1=0.979，ξ2=0.203

因为只有0＜ξ＜0.707时存在谐振峰值，故应选ξ=0.203。

于是，所测系统的传递函数为

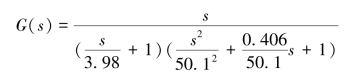
值得注意的是，实际系统并不都是最小相位系统，而最小相位系统可以和某些非最小相位系统具有相同的对数幅频特性曲线，因此具有非最小相位环节和延迟环节的系统，还需依据上述环节对相频特性的影响并结合实测相频特性予以确定。