优化闭环频率特性的文章标题

1.闭环频率特性

为了研究自动控制系统的性能指标，仅知道系统的开环频率特性是不够的。为此有必要进一步研究系统的闭环频率特性。控制系统的闭环频率特性可以通过闭环传递函数直接求得，也可以通过开环频率特性得到。

设控制系统的闭环传递函数为

式中，G（s）为前向通道的传递函数；H（s）为反馈通道的传递函数。

则闭环频率特性为

式中，M（ω）为闭环频率特性的幅值；φ（ω）为闭环频率特性的相位。

一般情况下，求解系统的闭环频率特性十分复杂，工程上通常采用向量法。

图4-46所示的单位反馈系统，其闭环传递函数为

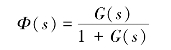
将s=jω代入上式，就可得到系统的闭环频率特性表示为

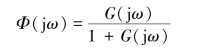
式中，G（jω）为单位负反馈系统的开环频率特性。

图4-46　单位反馈系统

设系统开环频率特性如图4-47所示。

图4-47　系统开环频率特性

以及

可见，只要给出系统开环频率特性G（jω），就可在ω=0→∞的范围内逐点绘制系统闭环频率特性。用这种方法求取闭环频率特性，几何意义清晰，容易理解，但过程较麻烦。

2.等M圆（等幅值轨迹）

将系统开环频率特性写成复数形式：G（jω）=P+jQ，则系统闭环频率特性(www.xing528.com)

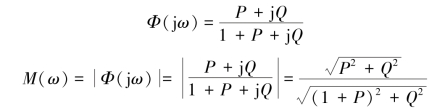
上式两边同时平方，整理可得

对于给定的M值，这是一个圆的方程。M为不同值时的一簇圆，称为G平面上的等M圆或等幅值轨迹，如图4-48所示。由图可看出，等M圆在G平面上是沿实轴对称的，它们的圆心均在实轴上。当M=1时，它是一条过点（-1/2，j0）且平行于虚轴的直线（无穷大圆弧）；当M＞1时，等M圆在P=-1/2直线的左边，随着M的增大，等M圆越来越小，最后收敛于（-1，j0）点。当M＜1时，等M圆在P=-1/2直线的右边，随着M的减小，等M圆越来越小，最后收敛于原点。

对单位反馈系统而言，根据G（jω）曲线与等M圆簇的交点得到对应的M值和ω值，便可绘制出闭环幅频特性M（ω）。

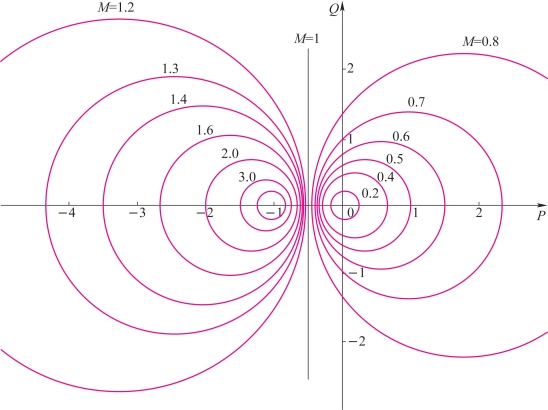
图4-48　等M圆

3.等N圆（等相位轨迹）

用类似的方法进一步研究系统闭环相频特性φ（ω）及其在G平面上的图形，有

上式也是一个圆的方程。当N或φ（N=tan φ（ω））为一定值时，它在G平面上是一个圆，改变N或φ的大小，它们在G平面上就构成了如图4-49所示的一簇圆，这簇圆的圆心都在虚轴左侧与虚轴距离为1/2且平行于虚轴的直线上，称这簇圆为等N圆或等相位轨迹。由图4-49可看出，等N圆中每个圆都通过坐标原点和（-1，j0）点，且等N圆实际上是等相位正切的圆，当相位增加±180°时，其正切相等，因而在同一个圆上。需要指出，等N圆实际上并不是一个完整的圆，而只是一段圆弧，例如φ（ω）=60°和φ（ω）=180°的圆弧是同一个圆的一部分。因此，用等N圆来确定闭环系统的相位时，就必须确定适当的φ值。应从对应于φ（ω）=0°的0频率开始，逐渐增加频率直到高频，所得到的闭环相频曲线应该是连续的。

对单位反馈系统而言，根据G（jω）曲线与等N圆簇的交点得到对应的N值和ω值，便可绘制出闭环相频特性φ（ω）。

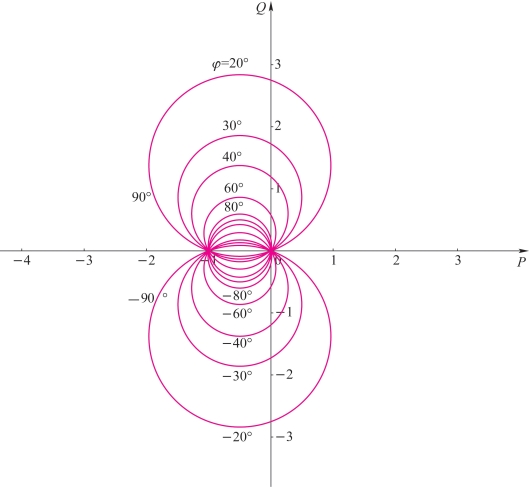
图4-49　等N圆

4.尼科尔斯（Nichols）图

尼科尔斯（Nichols）图，也称对数幅相频率特性图。它是将对数幅频特性和相频特性两条曲线合并成的一条曲线，是一种以ω为参变量，横坐标为相频特性（单位一般为°），纵坐标为对数幅频特性（单位一般为dB）的图示法，如图4-50所示。

图4-50　尼科尔斯（Nichols）图

尼科尔斯图由两簇曲线组成，一簇是对应于闭环频率特性的幅值（20lg M）为定值时的轨迹；另一簇则是对应于闭环频率特性的相位φ为定值时的轨迹。在绘有等M圆和等N圆的对数幅相平面上，画出系统的开环对数频率特性曲线。该曲线与等M圆和等N圆的交点即给出了每一频率下闭环系统的对数幅值和相位。

5.非单位反馈系统的闭环频率特性

上面以单位反馈系统为例，介绍了利用等M圆和等N圆求取闭环频率特性的方法。对于一般的非单位反馈系统，如图4-51（a）所示，可等效成如图4-51（b）所示的方框图，其中单位反馈部分的闭环频率特性可按上述方法求取，再与频率特性1/H（jω）相乘，即可得到总的闭环频率特性。

图4-51　非单位反馈控制系统

（a）一般非单位反馈系统方框图；（b）等效方框图