Bode稳定性判据：基本原理与应用

开环频率特性G（jω）H（jω）可以用奈氏图表示，也可以用Bode图表示，这两种图形有如下对应关系。

（1）奈氏图上的单位圆（圆心为坐标原点，半径为1），在Bode图的幅频特性上是零分贝线，因为单位圆上故

（2）奈氏图上的负实轴在Bode图的相频特性上是-180°水平线，因为负实轴上的点，相位是-180°。

根据上边“穿越”的概念，开环奈氏图对（-1，j0）以左的实轴穿越时，G（jω）H（jω）向量应具备两个条件：幅值大于1，相位等于-180°。把这两个条件转换在开环Bode图上，就是L（ω）＞0 dB时，相频曲线穿过-180°线一次，称为一次穿越，L（ω）＜0 dB时无所谓“穿越”。

正穿越为角度增大，在奈氏图上，自上而下穿过时幅角增大为正穿越。在Bode图上，L（ω）＞0dB下的相频曲线自下而上穿过-180°线时幅角增大为正穿越，反之，相频曲线由上而下穿过-180°线角度减小，为负穿越。

根据上述对应关系，对数频率特性的奈氏判据表述如下。

系统稳定的充要条件是：在开环Bode图上L（ω）＞0 dB的所有频段内，相频特性曲线φ（ω）在-180°线上正负穿越次数之差等于P/2。

如果恰在L（ω）=0 dB处相频曲线穿过-180°线，系统是临界稳定状态。

用上述判据可知图4-42所示两个开环Bode图对应的系统，在闭环状态下都是稳定的。

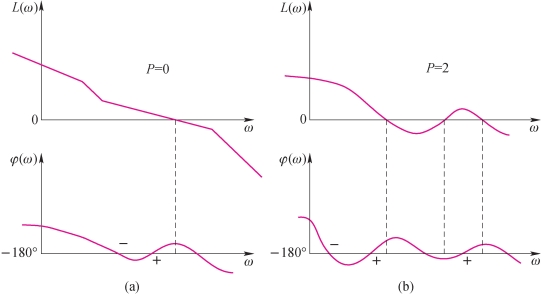
图4-42　开环Bode图(www.xing528.com)

遇到开环传递函数中含有积分环节时，应当按128页2）中所述开环有s=0的极点的情况处理，将Bode图中对数相频曲线的起始端（ω→0端）与其他环节（除去积分环节）在ω→0时的相位和φ0连接起来，再检查是否穿越-180°线。此时如果φ0起于-180°，算半次穿越，其正负仍按相位增加为正，相位减小为负。举例说明如下。

【例4-9】试用Bode图判断具有下列开环传递函数的非最小相位系统的稳定性。

解　（1）传递函数化成标准形式

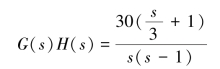
（2）作出开环Bode图。把开环传递函数分解成4个基本环节：①放大环节K=30，20 lg 30=29.5 dB；②积分环节1/s；③一阶微分环节（s/3+1），转折频率为3，其相频曲线如图4-43中曲线③所示；④一阶不稳定环节1/（s-1），转折频率为1，它的幅值与惯性环节1/（s+1）的幅值相同，但ω从0→∞变化时1/（s-1）的幅角是由-180°变化到-90°，其相频曲线如图4-43中曲线④所示。在图4-43中画出G（jω）H（jω）的对数幅频渐近线[图中标以L（ω）]和对数相频特性曲线[图中标以φ（ω）]。

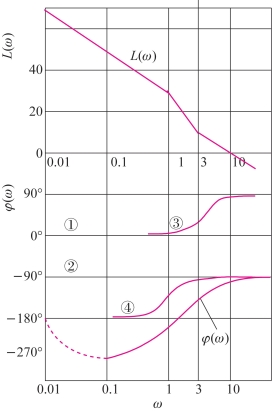
图4-43　的Bode图

（3）判断闭环系统的稳定性。

开环传递函数中有一个右极点，P=1。

根据上述奈氏判据检查L（ω）＞0 dB的频率范围内相频曲线在-180°线上的穿越情况。相频曲线起于-270°线，终于-90°线，有一次正穿越。但此时应考虑开环传递函数中有s=0的极点的情况，须做相应的处理。该系统开环传递函数中含有一个积分环节，而其他3个环节在ω→0时的相位和为φ0=-180°。所以应当由-180°与相频特性起始端连起来再进行判断。连接部分如图4-42中虚线所示，它相当于开环奈氏图中的辅助线（增补段）。经过增补以后的相频曲线起于-180°线向下行，所以计入半次负穿越。最后按稳定判据：正穿越次数-负穿越次数=1-1/2=P/2，所以，这个非最小相位系统是稳定的。但是，若不按开环有s=0极点的情况处理，必然得到错误的结果。