如何使用Nyquist稳定判据

前面介绍的稳定性判据，都是基于系统的微分方程或传递函数等参数模型。但在工程中，比较原始、直接的资料是用实验得到的频率特性等实验数据，而且，频率特性具有更清晰的物理意义。所以，工程技术人员更希望直接用实验得到的系统频率特性等来分析、设计系统。1932年，美国贝尔（Bell）实验室的Nyquist提出了一种应用开环频率特性曲线来判别闭环系统稳定性的判据，即Nyquist稳定判据，简称奈氏判据。

在系统初步设计和校正中经常采用频率特性的图解方法，这就为用Nyquist图或Bode图判断系统的稳定性带来了方便。因为这时系统的参数尚未最后确定，一些元件的数学表达式常常是未知的，仅有在实验中得到的频率特性曲线可供采用。应用奈氏判据，无论是由解析法还是由实验方法获得的开环频率特性曲线，都可用来分析系统的稳定性。

奈氏判据仍是根据系统稳定的充分必要条件导出的一种方法。欲使系统稳定，必须满足系统特征方程的根（即闭环极点）全部位于[s]平面的左半部，奈氏判据正是将开环频率特性G（jω）H（jω）与系统的闭环极点联系起来的判据。

利用奈氏判据不但可以判断系统是否稳定（绝对稳定性），也可以确定系统的稳定程度（相对稳定性），还可以用于分析系统的动态性能以及指出改善系统性能指标的途径。因此，奈氏判据是一种重要而实用的稳定性判据，工程上应用十分广泛。

1.理论基础

由于闭环系统的稳定性取决于闭环特征根的性质，因此，运用开环频率特性研究闭环系统的稳定性时，首先应明确开环频率特性与闭环特征方程之间的关系，然后，进一步寻找它与闭环特征根之间的规律性。

假设控制系统的一般结构方框图如图4-27所示。

图4-27　控制系统的一般结构方框图

系统的开环传递函数为

式中M（s）、N（s）为s的多项式，其s的最高幂次分别为m、n，且n≥m。

闭环特征方程可写成

可见，N（s）及N（s）+M（s）分别为开环和闭环特征多项式。将它们的特征多项式联系起来，引入辅助函数F（s），即

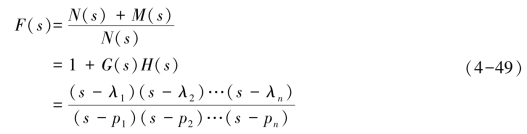
以s=jω代入上式，则有

式（4-49）和式（4-50）确定了系统开环频率特性和闭环特征多项式之间的关系。可以看出，1+G（s）H（s）的极点pi（i=1，2，…，n）即开环传递函数G（s）H（s）的极点；而1+G（s）H（s）的零点λi（i=1，2，…，n）正是闭环传递函数的极点，建立这个关系是证明奈氏判据的第一步。

奈氏判据的理论基础是复变函数中的幅角定理，也称映射定理，它是幅角定理在工程控制中的具体应用，下面首先介绍幅角定理。

假设复变函数F（s）为单值，且除了[s]平面上有限的奇点外，处处都为连续的正则函数，也就是说F（s）在[s]平面上除奇点外处处解析，那么，对于[s]平面上的每一个解析点，在[F（s）]平面上必有一点（称为映射点）与之对应。

例如，系统的开环传递函数为

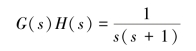
其辅助函数是

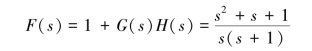
除奇点s=0和s=-1外，在[s]平面上任取一点，如

则

如图4-28所示，在s=-10平面上有点F（s1）=0.95-j0.15与[s]平面上的点s1对应，F（s1）就叫作s1=1+j2在[F（s）]平面上的映射点。

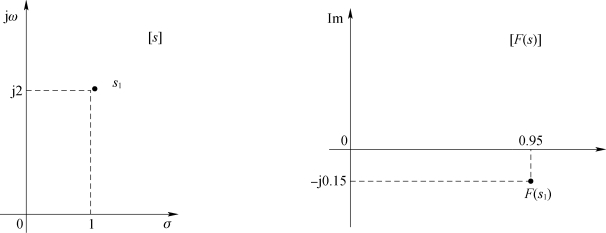
图4-28　[s]平面上的点在[F（s）]平面上的映射

（a）[s]平面；（b）[F（s）]平面

如果解析点s1在[s]平面上沿封闭曲线ΓS（ΓS不经过F（s）的奇点）按顺时针方向连续变化一周，那么辅助函数F（s）在[F（s）]平面上的映射也是一条封闭曲线ΓF，但其变化方向可以是顺时针的，也可以是逆时针的，这要依据辅助函数F（s）的性质而定，如图4-29所示。

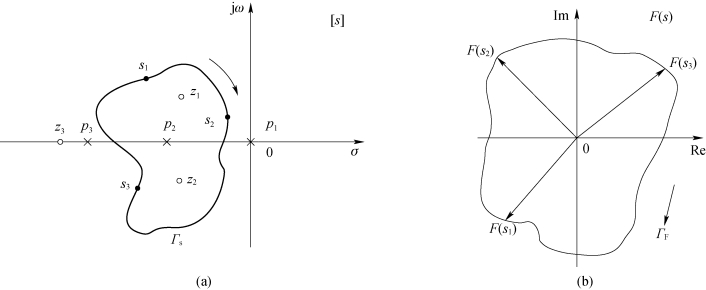
图4-29　[s]平面到[F（s）]平面的映射

（a）[s]平面；（b）[F（s）]平面

幅角定理（映射定理）：设F（s）在[s]平面上，除有限个奇点外，为单值的连续正则函数，若在[s]平面上任选一封闭曲线ΓS，并使ΓS不通过F（s）的奇点，则[s]平面上的封闭曲线ΓS映射到[F（s）]平面上也是一条封闭曲线ΓF。当解析点s按顺时针方向沿ΓS变化一周时，则在[F（s）]平面上，ΓF曲线按逆时针方向旋转的周数N（每旋转2π弧度为一周），或ΓF按逆时针方向包围[F（s）]平面原点的次数，等于封闭曲线ΓS内包含F（s）的极点数P与零点数Z之差。即

式中，若N＞0，则ΓF按逆时针方向绕[F（s）]平面坐标原点N周；若N＜0，则ΓF按顺时针绕[F（s）]平面坐标原点N周；若N=0，则ΓF不包围[F（s）]平面坐标原点。

在图4-29中，[s]平面上有3个极点p1、p2、p3和3个零点z1、z2、z3。被ΓS曲线包围的零点有z1、z2两个，即Z=2，包围的极点只有p2，即P=1，则

说明ΓS映射到[F（s）]平面上的封闭曲线ΓF顺时针绕[F（s）]平面原点一周。

由幅角定理，我们可以确定被封闭曲线ΓS所包围的辅助函数F（s）的极点数P与零点数Z的差值（P-Z）。

封闭曲线ΓS和ΓF的形状是无关紧要的，因为它不影响上述结论。

关于幅角定理的数学证明请读者参考有关书籍。

2.Nyquist轨迹及其映射

为了分析反馈控制系统的稳定性，只需判断是否存在[s]平面右半部的闭环极点。根据复变函数中的保角映射关系，对于[s]平面上的一条连续封闭曲线，在[1+G（s）H（s）]平面上必有一条封闭曲线与之对应。在证明奈氏判据时，取[s]平面上的封闭曲线ΓS，包围整个[s]平面的右半部，即沿着虚轴由-j∞→+j∞，再沿着半径为∞的半圆构成封闭曲线，如图4-30所示。

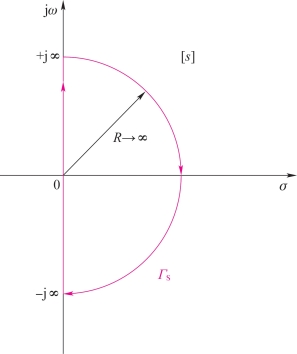
图4-30　[s]平面上的封闭曲线

若将F（s）=1+G（s）H（s）的零点zi（i=1，2，…，n）和极点pi（i=1，2，…，n）画在[s]平面上，那么，F（s）实部为正的极点和零点都被封闭曲线ΓS包围进去，即ΓS包围了系统所有实部为正的开环极点和闭环极点（下面简称开环右极点和闭环右极点）。

下面来看ΓS的映射曲线ΓF。

ΓS由两部分曲线组成，一部分为[s]平面上沿虚轴的部分，另一部分为无穷大半圆部分。按照幅角定理，这两部分曲线都将映射到F（s）平面上，共同构成ΓF，按照ΓF绕F（s）平面原点的旋转情况即可确定包围次数N。

（1）当ΓS为[s]平面上沿虚轴的部分，变量s沿[s]平面的虚轴从-∞到+∞变化时，即s=jω，映射到[1+G（s）H（s）]平面上就是1+G（jω）H（jω）曲线。而G（jω）H（jω）曲线正是系统的开环奈氏图。

在平面[1+G（s）H（s）]和[G（s）H（s）]之间的实轴坐标相差1，[1+G（s）H（s）]平面（简写为[1+GH]平面）的坐标原点正是[G（s）H（s）]平面（简写为[GH]平面）上的（-1，j0）点。如果由ΓS映射的曲线在[1+GH]平面上包围其坐标原点，在[GH]平面上则包围（-1，j0）点，即当1+G（jω）H（jω）=0时，有G（jω）H（jω）=-1。

（2）曲线的另一部分即无穷大半圆部分，此时

故ΓS无穷大半圆部分映射到[GH]平面上为坐标原点（当n＞m时），或[GH]平面的实轴上某定点K（当n=m时），这两种情况都对某点的包围情况不构成影响。

所以ΓF的绕行情况只需考虑G（jω）H（jω）开环奈氏图。

3.Nyquist稳定判据

前面已经指出，F（s）的极点数等于开环传递函数G（s）H（s）的极点数，因此当从[F（s）]平面上确定了封闭曲线ΓF的旋转周数N以后，则在[s]平面上封闭曲线ΓS包含的零点数Z（即系统的闭环极点数）便可简单地由下式计算出来

式中，Z为闭环右极点个数，正整数或0；P为开环右极点个数，正整数或0；N为ω从-∞→+∞变化时，G（jω）H（jω）封闭曲线在[GH]平面内包围（-1，j0）点的次数。当N＞0时，是按逆时针方向包围的情况；当N＜0时，是按顺时针方向包围的情况；当N=0时，表示曲线不包围（-1，j0）点。

由式（4-53），则可根据开环右极点个数P和开环奈氏图对（-1，j0）点的包围次数N，来判断闭环右极点数Z是否等于0。若要系统稳定，闭环不能有右极点，即必须使Z=0，也就是要求N=P。令开环传递函数G（s）H（s）的分母为0，可求得开环右极点数；N的确定则须画出开环奈氏图，ω从-∞→0→+∞的开环奈氏图是一条关于实轴对称的封闭曲线，只要画出ω从0→∞的那一半曲线，按镜像对称原则便可得到ω从-∞→0的另一半曲线，如图4-31所示。奈氏图对（-1，j0）点的包围情况N即可得出。有了P和N，便可确定Z。

图4-31　ω从-∞→∞的奈氏图

为了简单起见，通常只画出ω从0→∞的G（jω）H（jω）曲线，当仅用正半部分奈氏图判别系统的稳定性时，包围次数应当增加一倍才符合式（4-53）的关系，即把式（4-53）改写为

式中，N为ω从0→∞的G（jω）H（jω）曲线对（-1，j0）点包围的次数，N的正负及P、Z的意义同式（4-53）。

按式（4-54），闭环系统稳定时，即当Z=0时应满足

或

归纳上述，按式（4-56）的关系给出奈氏判据的结论：当ω从0→∞变化时，开环频率特性曲线G（jω）H（jω）逆时针包围点（-1，j0）的次数N如果等于开环右极点数的一半P/2，则闭环系统是稳定的，否则系统不稳定。

应用奈氏判据判断系统稳定性的一般步骤如下。

（1）绘制ω从0→∞变化时的开环频率特性曲线，即开环奈氏图，并在曲线上标出ω从0→∞增加的方向。根据曲线包围（-1，j0）点的次数和方向，求出N的大小及正负。为此可从（-1，j0）点向G（jω）H（jω）曲线上作一矢量，并计算当ω从0→∞变化时这个矢量相应转过的“净”角度，规定逆时针旋转方向为正角度方向，并按转过360°折算N=1，转过-360°折算N=-1。要注意N的正、负及N=0的情况，N的计算如图4-32所示。

图4-32　N的计算

（a）N=-1；（b）N=0

（2）由给定的开环传递函数确定开环右极点数P，并按奈氏判据判断系统的稳定性。若N=P/2，则闭环系统稳定，否则不稳定。如果-ωτ曲线刚好通过（-1，j0）点，表明闭环系统有极点位于虚轴上，系统处于临界稳定状态，归入不稳定情况。

4.应用举例

在应用奈氏判据时，根据开环传递函数是否包含s=0的极点（即开环传递函数中是否包含积分环节），可分为以下两种情况。

1）开环传递函数中没有s=0的极点

【例4-4】单位负反馈系统的开环传递函数为

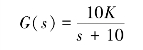
试用奈氏判据判断K=4和K=-4情况下系统的稳定性。

解　作出K=4和K=-4时的开环奈氏图，如图4-33所示。

K=4时，开环奈氏图如图4-33（a）所示，可以明显看出曲线不包围（-1，j0）点，所以N=0。由开环传递函数可知，开环极点为s=-10，因此开环无右极点，P=0。(www.xing528.com)

由奈氏判据知，系统在K=4时是稳定的。

图4-33　的奈氏图

（a）K=4；（b）K=-4

当K=-4时，开环奈氏图如图4-33（b）所示，这时开环极点没有变化，但曲线顺时针包围（-1，j0）点半周，即

可见在K=-4时系统不稳定。

例4-4说明，系统在开环无右极点的情况下，闭环是否稳定须用判据判断以后才能知道，并不存在开环稳定（P=0），闭环一定稳定的必然关系。

【例4-5】已知单位反馈系统开环传递函数

试判别闭环系统的稳定性。

解　作出开环奈氏图，如图4-34所示。由图可见，G（jω）正向包围（-1，j0）点半圈，即N=1/2；由G（s）可知开环是不稳定的，有一个正根，即P=1，故N=P/2，闭环系统稳定。

图4-34　的奈氏图

从例4-4、例4-5可以看出，开环系统稳定，但若各部件以及被控对象的参数选择不当，很可能保证不了闭环系统的稳定性；而开环系统不稳定，只要合理地选择控制装置，完全能使闭环系统稳定。

【例4-6】设系统的开环传递函数为

判断闭环系统的稳定性。

解　系统的开环频率特性为

当ω=0时

当ω=∞时

该系统开环奈氏图的大致形状如图4-35所示。曲线从正实轴上的K点开始，顺时针旋转穿过3个象限，沿-270°线终止于原点。K值较小时，如曲线①所示，不包围（-1，j0）点，N=0。

图4-35　三阶系统的开环奈氏图

当K值增大到K′，曲线的相位不变，仅幅值增大，如曲线②所示，顺时针包围（-1，j0）点一周，即N=-1。因为开环无右极点，P=0。所以，在曲线①所示情况下，闭环系统稳定，在曲线②所示情况下，系统不稳定。可见开环增益K的增大，不利于系统的稳定性。从系统稳态误差的角度来说，K的增大有利于稳态误差的减小。为了兼顾精度和稳定性，需要在系统中加补偿环节。

2）开环传递函数中有s=0的极点

当系统中串联有积分环节，即开环传递函数有s=0的极点时，需将奈氏判据进行如下处理。

在[s]平面上的封闭曲线ΓS向[1+GH]平面上映射时，ΓS是沿虚轴前进的，现在原点处有极点，ΓS曲线应以该点为圆心，以无穷小为半径的圆弧按逆时针方向绕过该点，如图4-36所示。由于绕行半径为无限小，因此可以认为所有不在原点上的右极点和右零点仍能被包括在ΓS封闭曲线之内。这时开环右极点数P已不再包含s=0处的极点。

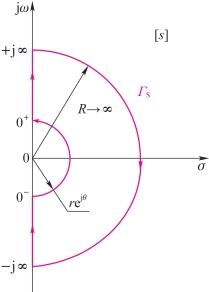
图4-36　[s]平面上避开原点上极点的封闭曲线

由于积分环节在ω=0时的相位为-90°，幅值为∞，其影响将使含有积分环节的开环奈氏图在ω=0时的起点不是实轴上的一个定值点，而是沿某一个坐标轴趋于∞，如图4-37中的实线所示。因此ω从-∞→+∞的开环奈氏图不封闭，无法识别曲线对（-1，j0）点的包围情况。遇到这种情况，可以作辅助曲线，如图4-37中的虚线所示。

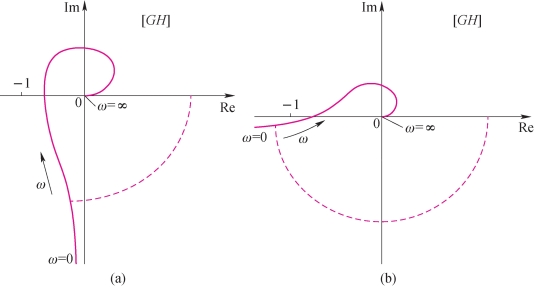
图4-37　含有积分环节的开环奈氏图

辅助曲线的作法如下：以无穷大为半径，从奈氏图的起始端沿逆时针方向绕过ν·90°作圆和实轴相交，这个圆就是辅助曲线，ν是开环传递函数中含有积分环节的个数。

设系统的开环传递函数为

式中，ν为开环传递函数中含有积分环节的个数。当s沿无穷小半圆逆时针方向移动时，有

将式（4-58）代入式（4-57）中，得

根据式（4-59）可以确定当s沿小半圆从ω=0-变化到ω=0+时，[s]平面上半径为无穷小的圆弧映射在[GH]平面上为无限大半径的圆弧，幅角由φ0变化ν·（-90°），此无限大半圆即为开环奈氏图的辅助线，其起点始于坐标轴，终点即为G（jω）H（jω）开环奈氏图的起点，如图4-37中的虚线所示。

经过以上的处理，原开环奈氏图和辅助曲线一起构成封闭映射曲线，由此可以判断封闭映射曲线对（-1，j0）点的绕行情况，故原奈氏判据仍可使用。

例如，图4-37中的两个系统，开环均无右极点，即P=0，增补（加辅助线）后的开环奈氏图又都不包围（-1，j0）点，故N=0，所以由奈氏判据可以判断两个系统都是稳定的。

【例4-7】设某非最小相位系统的开环传递函数为

试判断该系统的稳定性。

解　作出开环奈氏图如图4-38所示，根据作辅助线的方法，由奈氏图的起始端（ω=0端），以无穷大为半径，沿反时针方向旋转90°，交于负实轴，形成图中的虚线部分。注意，此处没有交于正实轴，是因为开环传递函数中只一个积分环节，ν=1，辅助线只有90°范围的幅角，而除去积分环节的其他环节在ω=0时的相位和φ0=-180°。在确定奈氏图包围（-1，j0）点的次数和方向时，应将虚线和实线连续起来看，整个曲线的旋转方向仍按ω增大的方向。这样，由图4-38可以看出，曲线顺时针包围（-1，j0）点半圈，即N=-1/2。

图4-38　的奈氏图

检查开环极点：s1=0，s2=1/T，其中s2是正实数，是一个右极点，而s1=0，不算右极点。所以开环右极点数P=1，由奈氏判据可知系统不稳定。

【例4-8】Ⅱ型系统开环传递函数为

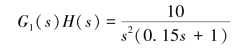
试判断闭环系统的稳定性。

解　作出开环奈氏图如图4-39（a）所示，由图知N=-1，即顺时针包围（-1，j0）点一周。

开环传递函数无右极点，P=0。所以系统不稳定。

如果在原系统中串入一个一阶微分环节（2.5s+1），使开环传递函数变成

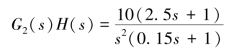
利用一阶微分环节的正相位角度，使原开环频率特性的相位滞后量减小，在开环奈氏图上希望曲线不要到达第二象限，只在第四、第三象限就不会包围（-1，j0）点，其开环奈氏图如图4-39（b）所示。

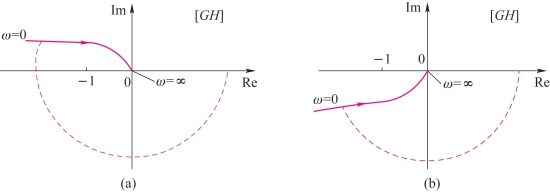
图4-39　例4-8的开环奈氏图

（a）G1（jω）H（jω）；（b）G2（jω）H（jω）

这一例子说明，通过串联一阶微分环节的“校正”作用，有可能使Ⅱ型系统变得稳定。

3）开环频率特性曲线比较复杂时奈氏判据的应用

如图4-40所示的复杂的开环奈氏图，若用对（-1，j0）点的包围圈数来确定N，就很不方便，为此引出“穿越”的概念。

所谓“穿越”，指开环奈氏图穿过（-1，j0）点左边的实轴部分。若曲线由上而下穿过-1→-∞实轴段时称“正穿越”，曲线由下而上穿过时称“负穿越”。穿过（-1，j0）以左的实轴一次，则穿越次数为1，若曲线始于或止于（-1，j0）以左的实轴上，则穿越次数为1/2。

图4-40　复杂的开环奈氏图

正穿越相当于奈氏图逆时针包围（-1，j0）点，对应相位增大；负穿越相当于曲线顺时针包围（-1，j0）点，对应相位减小。注意，曲线穿过（-1，j0）点以右的实轴不称为穿越。

这样，奈氏判据可以写成：当ω从0变到∞时，若开环频率特性曲线在（-1，j0）点以左实轴上的正穿越次数减去负穿越次数等于P/2，则闭环系统是稳定的，否则不稳定。其中P为开环右极点数。

应用这个判据可判断图4-40所示系统的稳定性，给定系统开环右极点数P=2。由图看出，正穿越次数为2，负穿越次数为1。正穿越次数减去负穿越次数等于P/2，所以闭环系统稳定。

4）延时系统稳定性的判别

设带有延时环节的反馈控制系统的开环传递函数为

式中，G1（s）H1（s）为除去延时环节的开环传递函数；τ为延迟时间，单位s。上式表明延时环节在前向通道或在反馈通道中串接，对系统的稳定性影响是一样的。

延时环节e-τs的频率特性e-jωτ的幅值为1，相位为-ωτ。有延时环节的开环频率特性及幅频、相频特性为

可见有延时环节对G1（jω）H1（jω）的幅值无影响，只是相位比对应的没有延时环节的系统要滞后，也就是使G1（jω）H1（jω）向量在每一个ω上都按顺时针方向旋转ωτ弧度。

应用有延时环节的开环奈氏图判断闭环系统稳定性的方法，和上述奈氏判据的用法是一样的。例如，有延时环节的系统，其开环传递函数是

系统中加入延时环节e-τs后，开环奈氏图随着延时时间常数τ取值的不同而变化，在图4-41中画出τ取不同值时的3条曲线进行对比。

图4-41　的奈氏图

由图可见，τ=0时，也就是没有延时环节存在时，闭环系统是稳定的。随着τ的增大，系统的稳定性变差，当τ=2 s时，G（jω）H（jω）曲线通过（-1，j0）点，系统处于临界稳定状态。τ=4 s时，系统变得不稳定。延时环节常常使系统的稳定性变差，而实际系统中又经常不可避免地存在延时环节，延迟时间τ短则几毫秒，长则数分钟，为了提高系统的稳定性，应当尽量减小延迟时间。