开环频率特性与闭环系统性能的关系

系统开环频率特性的求取比闭环频率特性的求取方便，且对于最小相位系统，幅频特性和相频特性之间有确定的对应关系，因此，可由开环频率特性来分析和设计系统的动态响应和稳态性能。

实际系统的开环对数幅频特性L（ω）一般都符合如图4-26所示的特征：左端（频率较低的部分）高；右端（频率较高的部分）低。可将L（ω）人为地分为3个频段：低频段、中频段和高频段。需要指出的是，3频段的划分是相对的，各频段之间没有严格的界限。但它反映了对控制系统性能影响的主要方面，为进一步确定开环频域指标和闭环系统性能之间的关系，指出了原则和方向。

开环对数频率特性的3个频段包含了闭环系统性能不同方面的信息，即低频段、中频段和高频段分别表征了系统的稳定性、动态特性和抗干扰能力。下面分别进行讨论。

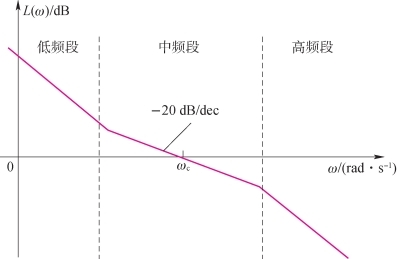
图4-26　开环对数幅频特性3频段的划分

1.低频段与稳态精度

在对数频率特性图中，低频段通常是指L（ω）曲线在第一个转折频率以前的频段。此段的特性由开环传递函数中的积分环节和开环增益决定。设低频段对应的开环传递函数为

由3.5节可知，系统稳态精度，即稳态误差ess的大小，取决于系统的开环增益K和系统的型别（积分环节个数ν）。而积分环节个数ν决定着低频渐近线的斜率，开环增益K则决定着渐近线的高度。因此，开环对数幅频特性的低频渐近线斜率越大（指绝对值）、位置越高，对应的开环系统积分环节个数ν越多、开环增益K越大，系统的稳态误差ess越小、稳态精度越高。

2.中频段与动态性能

在对数频率特性图中，中频段是指L（ω）在开环截止频率ωc（即穿越0 dB线的频率）附近的频段，这段特性集中反映闭环系统动态响应的平稳性和快速性。

下面对对数幅频特性中频段的斜率和宽度分两种情况进行分析。

（1）中频段斜率为-20 dB/dec。设L（ω）曲线中频段斜率为-20 dB/dec，且有较宽的频率区域，其对应的开环传递函数可近似为

若系统为单位反馈系统，则闭环传递函数为(www.xing528.com)

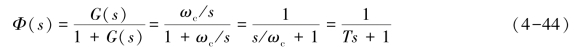
式中，T=1/ωc为时间常数。

此时系统相当于一个一阶系统，其阶跃响应按指数规律变化，没有振荡，即具有较高的稳定程度，且ts=（3～4）/ωc，ωc越大，ts越小，系统的快速性越好。

（2）中频段斜率为-40 dB/dec。设L（ω）曲线中频段斜率为-40 dB/dec，且有较宽的频率区域，其对应的开环传递函数可近似为

若系统为单位反馈系统，则闭环传递函数为

此时系统相当于ξ=0的二阶系统，系统处于临界稳定状态，动态过程持续振荡。因此，中频段斜率如为-40 dB/dec，所占区域不宜太宽，否则σ%、ts显著增大。

若中频段斜率小于-40 dB/dec时，闭环系统将难以稳定，因此，通常中频段斜率取-20dB/dec，且应占有一定的频域宽度，即可获得较好的稳定性，依靠提高开环截止频率ωc，获得较好的快速性。

3.高频段与动态性能

在对数频率特性图中，高频段通常是指L（ω）曲线在ω＞10ωc以后的频段。这部分特性是由系统中时间常数很小且频带很高的部件决定的。由于远离ωc，一般分贝值又较低，故对系统动态性能影响不大，近似分析时，可将多个小惯性环节等效为一个小惯性环节，其时间常数等于被代替的多个小惯性环节的时间常数之和。

另外，从系统抗干扰性的角度看，高频段特性是有其意义的，由于高频部分的开环幅频特性曲线一般较低，即故对单位反馈系统，有

即在高频段，闭环幅频特性近似等于开环幅频特性。因此，开环对数幅频特性在高频段的幅值，直接反映了系统对高频干扰信号的抑制能力，高频部分的幅值越低，系统的抗干扰能力越强，即高频衰减能力越强。

综上所述，为了设计一个合理的控制系统，对开环对数幅频特性的形状要求如下：低频段要有一定的高度和斜率；中频段的斜率最好为-20 dB/dec，且具有足够的宽度；高频段采用迅速衰减的特性，以抑制不必要的高频干扰。