最小相位系统的特点和应用

为了说明幅频特性和相频特性之间的关系，在此提出最小相位系统概念。

在[s]平面的右半平面既无极点，也无零点的传递函数，称为最小相位传递函数；否则，称为非最小相位传递函数。具有最小相位传递函数的系统，称为最小相位系统。

例如，某两个单位反馈的控制系统的开环传递函数分别为

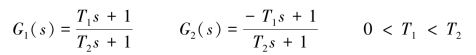
显然，G1（s）的零点为z=-1/T1，极点为p=-1/T2，如图4-22（a）所示。G2（s）的零点为z=1/T1，极点为p=-1/T2，如图4-22（b）所示。根据最小相位系统的定义，具有G1（s）的系统是最小相位系统，而具有G2（s）的系统是非最小相位系统。

图4-22　最小相位系统和非最小相位系统

（a）最小相位系统；（b）非最小相位系统

对于稳定系统而言，根据最小相位传递函数的定义可推知：最小相位系统的相位变化范围最小，这是因为(www.xing528.com)

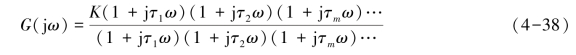
对于稳定系统，T1，T2，…，Tn均为正值，τ1，τ2，…，τm可正可负，而最小相位系统的τ1，τ2，…，τm均为正值，从而有

非最小相位系统，若有q个零点在[s]平面的右半平面，则有

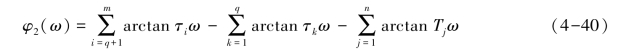
比较上面的两个相位表达式（4-39）和式（4-40）可知，稳定系统中最小相位系统的相位变化范围最小。在上例中，两个系统具有同一幅频特性，而相频特性却不同，两系统的Bode图如图4-23所示，这就说明了上述结论。最小相位系统的对数幅频特性渐近线在频率趋于无穷大时的斜率为-20（n-m）dB/dec（其中n、m分别为传递函数中分母、分子多项式的阶数），而对数相频特性在频率趋于无穷大时为-90°（n-m）。这个结论可以从图4-23验证。但是，满足这两个条件的系统并非都是最小相位系统，如传递函数为G3（s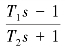）=的系统，在频率趋于无穷大时，对数幅频特性渐近线的斜率为0 dB/dec，满足斜率等于-20（n-m）dB/dec；对数相频特性为0°，也满足相位等于-90°（n-m）。但是很显然，该系统是非最小相位系统。

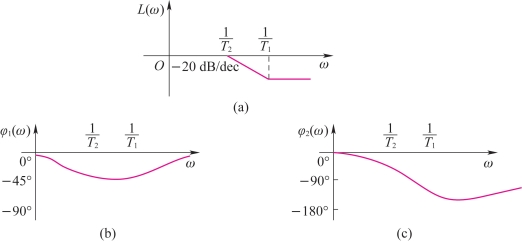
图4-23　最小相位系统和非最小相位系统的Bode图

（a）两系统的幅频特性图；（b）最小相位系统的相频特性图；（c）非最小相位系统的相频特性图