稳定性的概念及其重要性

任何系统在扰动作用下都会偏离原平衡状态，产生初始偏差。所谓稳定性就是指系统当扰动作用消失以后，系统能够以足够的精度由初始偏差状态逐渐恢复到原平衡状态的性能。若能恢复平衡状态，就称该系统是稳定的；若系统在扰动作用消失以后不能恢复平衡状态，且偏差越来越大，则称系统是不稳定的。

举例说明如下。图3-24（a）所示为一单摆系统，假设在外界扰动作用下，单摆由平衡位置a向左偏移到b，当外界扰动消失后，单摆在平衡位置a附近反复振荡，经过一定时间后，单摆最终重新回到平衡位置a，则单摆系统是稳定的。反之，如图3-24（b）所示的倒立摆系统，位置d是其平衡位置，当受到外界扰动作用后，倒立摆偏离平衡位置，且越偏越大，即使扰动消除后也不会回到原来的平衡位置d，则倒立摆系统是不稳定的。

系统在扰动作用消失后，能够随着时间推移恢复到原平衡状态的稳定性，称为渐进稳定性，这种稳定性是线性定常系统的一种特征。也就是说，线性定常系统如果是稳定的，必定是渐进稳定的。本节所讨论的稳定性，就是渐进稳定性。

由于系统稳定性反映的是扰动消除后，系统自身的一种恢复能力，所以稳定性是系统的固有特性，只取决于系统内部的结构和参数，而与初始状态和外作用的大小无关。

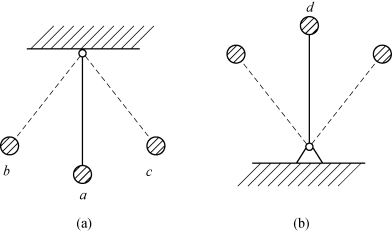
图3-24　稳定系统与不稳定系统

（a）单摆；（b）倒立摆

系统的稳定性又分绝对稳定性和相对稳定性。(www.xing528.com)

1.绝对稳定性

在研究控制系统时，需要根据对象和环节所遵循的物理或化学定律，预测系统的性能。系统的首要性能就是绝对稳定性，即系统是稳定的还是不稳定的。当控制系统没有受到任何扰动，也没有施加输入信号，系统的输出量保持在某一状态，这一状态称为控制系统的平衡状态。如果线性定常系统在输入或扰动的作用下，偏离了其平衡状态，当输入或扰动消失后，输出量最终返回其平衡状态，那么系统稳定；输出量呈现为持续不断的等幅振荡过程，则系统为临界稳定；输出量在输入作用下无限制地偏离其平衡状态（输出量发散），则系统不稳定。实际上，物理系统的输出量只能增大到一定的范围，此后或者受到机械制动装置的限制，或者系统遭到破坏，也可能当输出量超过一定数值后，系统变成非线性的，线性微分方程不再适用。

实际的物理控制系统包含有一些储能元件，当输入量作用于系统时，储能元件储存能量，系统的输出量不能立即跟随输入量的变化。稳定的系统在响应到达稳态之前，表现为瞬态响应过程，随着时间的推移消耗能量，系统逐渐进入稳态。在稳态响应过程，如果系统的输出量与输入量不能完全吻合，则称系统具有稳态误差。不稳定的系统在振荡过程中不断吸收能量，因而偏离稳态值越来越远。

绝对稳定性是系统能够正常工作的前提。

2.相对稳定性

当判断系统是绝对稳定的，接下来的重要问题是如何确定绝对稳定系统的稳定程度，稳定程度可利用相对稳定性来度量，即稳定性裕量。相对稳定性在第4章介绍，在这里不做赘述。

3.运动稳定性

运动稳定性的数学定义，是由俄国学者李雅普诺夫（A.M.Ляпунов，1857—1918）首先建立的，运动稳定性是物体或系统在外干扰的作用下偏离其运动后返回该运动的性质。若逐渐返回原运动则称此运动是稳定的，否则就是不稳定的。对任何运动，外干扰都是经常存在的，因此可以说，物体或系统的某一运动的稳定性就是它的存在性，只有稳定的运动才能存在。在工程技术上，要使设计对象的某些运动能够实现，那些运动必须是稳定的。李雅普诺夫稳定性原理是关于渐近稳定、稳定和不稳定的定理，奠定了稳定性理论的基础。该理论基于现代控制的状态空间理论，是针对单变量、多变量、线性、非线性、定常和时变系统的稳定性分析皆适用的通用方法，是现代稳定性理论的重要基础和现代控制理论的重要组成部分。这里不做介绍，读者如有兴趣可参看有关论著。