控制系统的性能指标是评价系统动态品质的定量指标,是定量分析的基础。性能指标往往用几个特征量来表示,既可以在时域提出,也可以在频域提出。时域性能指标比较直观,是以系统对单位阶跃输入信号的时间响应形式给出的,主要有上升时间tr、峰值时间tp、最大超调量MP、调整时间ts以及振荡次数N等,如图3-20所示。
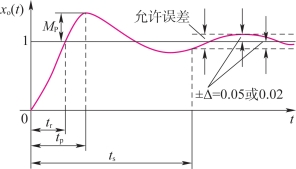
图3-20 控制系统的时域性能指标
1.上升时间tr
响应曲线从零时刻出发至首次到达稳定值所需的时间称为上升时间tr。对于没有超调的系统,从理论上讲,其响应曲线到达稳态值的时间需要无穷大,因此,一般将其上升时间tr定义为响应曲线从稳态值的10%上升到稳态值的90%所需的时间。
二阶系统在欠阻尼状态下的单位阶跃响应由式(3-40)给出,即
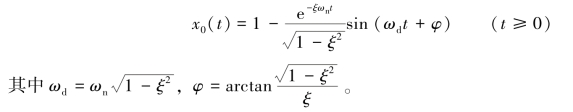
根据上升时间tr的定义,有xo(tr)=1代入上式,可得
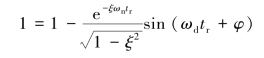
即

故有
![]()
由于tr被定义为第一次到达稳态值的时间,因此上式中应取k=1,于是得
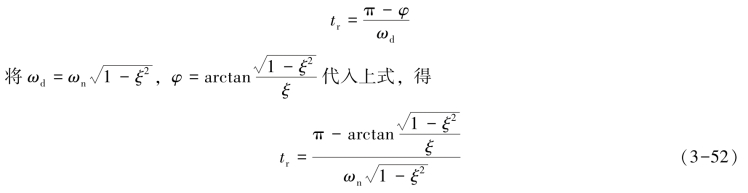
由上式可见,当ξ一定时,ωn增大,tr就减小;当ωn一定时,ξ增大,tr就增大。
2.峰值时间tp
响应曲线从零时刻出发至首次到达第一个峰值所需的时间,称为峰值时间tp。

从而有
![]()
由于tp被定义为到达第一个峰值的时间,因此上式中应取k=1,于是得

由此式可见,当ξ一定时,ωn增大,tp就减小;当ωn一定时,ξ增大,tp就增大。tp与tr随ωn和ξ的变化趋势相同。
将有阻尼振荡周期定义为
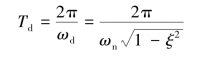
则峰值时间tp是有阻尼振荡周期Td的一半。
3.最大超调量MP
响应曲线的最大峰值与稳态值的差称为最大超调量MP,即
![]()
或者用百分数(%)表示
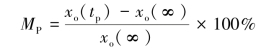
根据最大超调量MP的定义,将峰值时间![]() 代入上式,整理后可得
代入上式,整理后可得
![]()
由此式可见,最大超调量MP只与系统的阻尼比ξ有关,而与固有频率ωn无关,所以MP是系统阻尼特性的描述。因此,当二阶系统的阻尼比ξ确定后,就可以求出相应的最大超调量MP;反之,如果给定系统所要求的最大超调量MP,则可以由它来确定相应的阻尼比ξ。MP与ξ的关系如表3-2所示。
表3-2 MP与ξ的关系

由式(3-54)和表3-2可知,阻尼比ξ越大,最大超调量MP就越小,系统的平稳性就越好。当取ξ=0.4~0.8时,相应的MP=(25.4~1.5)%。
4.调整时间ts
在响应曲线的稳态值上,用±Δ作为允许误差范围,响应曲线到达并将永远保持在这一允许误差范围内所需的时间称为调整时间ts,允许误差范围±Δ一般取稳态值的±5%或±2%。(https://www.xing528.com)
在欠阻尼状态下,二阶系统的单位阶跃响应是幅值随时间按指数衰减的振荡过程,响应曲线的幅值包络线为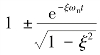 ,整个响应曲线总是包容在这一对包络线之内,同时,这两条包络线对称于响应特性的稳态值,如图3-21所示。
,整个响应曲线总是包容在这一对包络线之内,同时,这两条包络线对称于响应特性的稳态值,如图3-21所示。
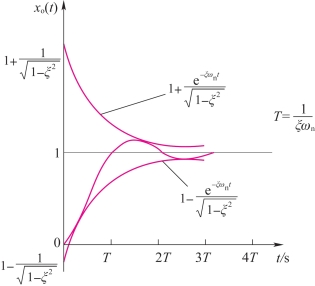
图3-21 二阶系统在欠阻尼状态下单位阶跃响应曲线的幅值包络线
响应曲线的调整时间ts可以近似地认为是响应曲线的幅值包络线进入允许误差范围±Δ之内的时间,因此有
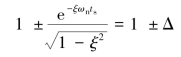
也即
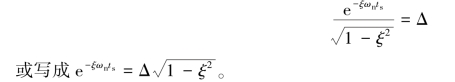
将上式两边取对数,可得
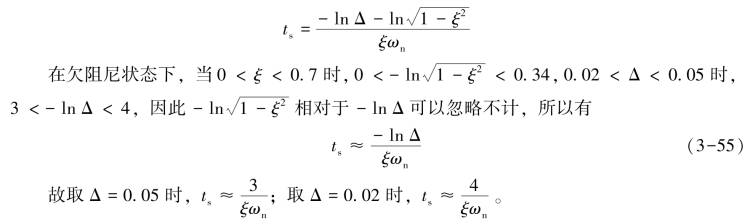
当ξ一定时,ωn越大,ts就越小,即系统的响应速度越快。若ωn一定,以ξ为自变量,对ts求极值,可得ξ=0.707时,ts为极小值,即系统的响应速度最快。而当ξ<0.707时,ξ越小则ts越大;当ξ>0.707时,ξ越大则ts越大。
5.振荡次数N
振荡次数N在调整时间ts内定义,实测时可按响应曲线穿越稳态值的次数的一半来计数。
以上各项性能指标中,上升时间tr、峰值时间tp、调整时间ts反映系统时间响应的快速性,而最大超调量MP和振荡次数N则反映系统时间响应的平稳性。
根据振荡次数N的定义,二阶系统的振荡次数N可以用调整时间ts除以有阻尼振荡周期Td来近似地求得,即
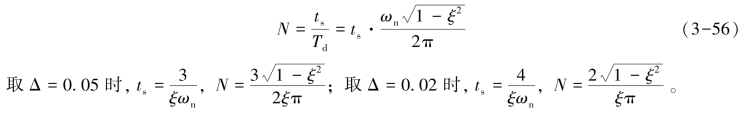
由此可见,振荡次数N只与系统的阻尼比ξ有关,而与固有频率ωn无关。阻尼比ξ越大,振荡次数N越小,系统的平稳性就越好。所以,振荡次数N也直接反映了系统的阻尼特性。
综上所述,二阶系统的固有频率ωn和阻尼比ξ与系统过渡过程的性能有着密切的关系。要使二阶系统具有满意的动态性能,必须选取合适的固有频率ωn和阻尼比ξ。增大阻尼比ξ,可以减弱系统的振荡性能,即减小超调量MP和振荡次数N,但是增大了上升时间tr和峰值时间tp。如果阻尼比ξ过小,系统的稳定性又不能符合要求。所以,通常要根据所允许的最大超调量MP来选择阻尼比ξ。阻尼比ξ一般选择在0.4~0.8之间,然后再调整固有频率ωn的值以改变瞬态响应时间。当阻尼比ξ一定时,固有频率ωn越大,系统响应的快速性越好,即上升时间tr、峰值时间tp和调整时间ts越小。
【例3-2】如图3-22所示的控制系统方框图,欲使系统的最大超调量等于0.2,峰值时间等于1 s,试确定增益K与Kh的数值,并确定在此K与Kh数值下,系统的上升时间tr和调整时间ts。
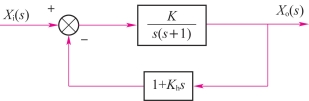
图3-22 控制系统方框图
解 依题意,有
![]()
解之得ξ=0.456。
依题意tp=π/ωd=1 s,则
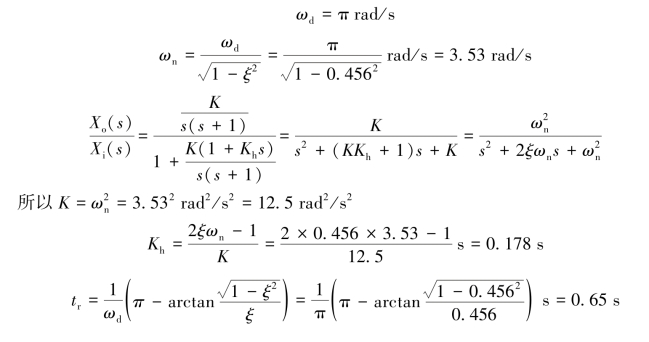
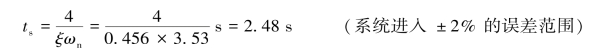
【例3-3】图3-23(a)所示为一机械系统,当在质量m上施加8.9 N的阶跃力后,记录其位移的时间响应曲线如图3-23(b)所示,试求该系统的质量m、弹性系数k和黏性阻尼系数c的数值。
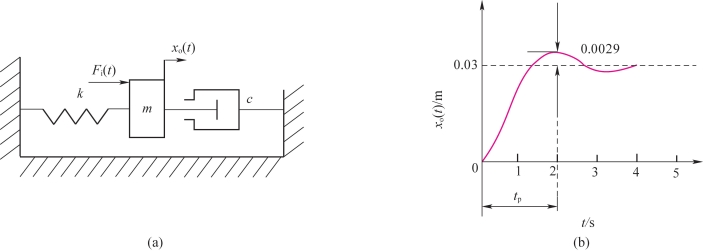
图3-23 机械系统及其响应曲线
(a)机械系统示意图;(b)位移的时间响应曲线
解 根据牛顿第二定律
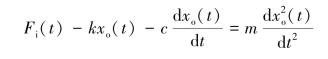
进行拉氏变换,并整理得
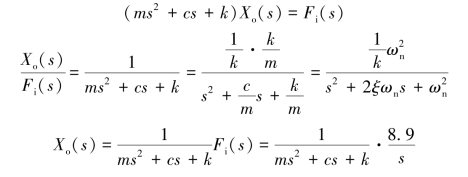
由终值定理得
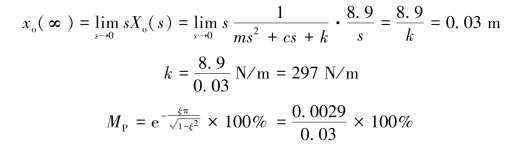
解得
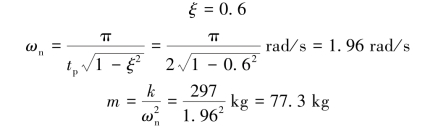
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




