二阶系统的数学描述简介

图3-9为一位置随动系统的原理图。这个系统的任务是控制工作台的转动装置，使其与输入位置相一致。系统的原理如下：用一对电位计组成的电位差计作为系统的误差检测装置，把输入的角位移θi与输出的角位移θo差值，转换为与其成正比的电压信号e。其中输入电位计电刷臂的位置，由输入装置确定；输出电位计电刷臂的位置，由输出轴的位置确定。电位差计输出端的误差信号e（即电压信号e）送入增益为KF的放大器放大，放大后的电压ua加在直流电动机的电枢电路上，用以驱动电动机。电动机励磁绕组上加有固定电压，即恒励磁。如果出现误差信号e，电动机就产生力矩，通过输出轴带动工作台转动，并最终使误差信号减小到0。由此得到该位置随机系统的结构方框图如图3-10所示。

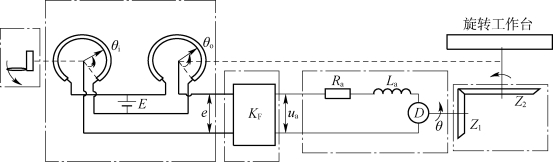
图3-9　位置随动系统的原理图

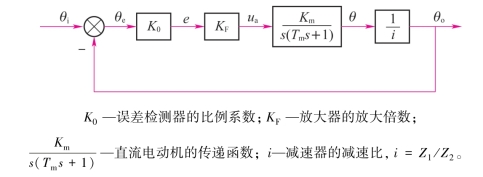
图3-10　位置随动系统结构方框图

由图3-10可得系统的开环传递函数为

令K=K0KFKm/i，则

由式（3-34）可得系统的闭环传递函数为

令其中ωn为无阻尼自然振荡角频率，ξ为阻尼比。则式（3-35）可写为

式（3-36）即为二阶系统传递函数的标准形式。既可以表示一个系统的闭环传递函数，也可以表示一个环节的传递函数。

位置随动系统的传递函数也可以图3-11所示的结构方框图表示，它也是典型的二阶系统模型。

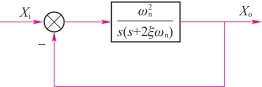
图3-11　二阶系统模型结构方框图

由式（3-36）可知，二阶系统的特征方程为(https://www.xing528.com)

两个特征根

显然，二阶系统的极点与二阶系统的阻尼比ξ和固有频率ωn有关，其中阻尼比ξ更为重要。随着阻尼比ξ取值的不同，二阶系统的极点在平面上的位置分布也各不相同。如图3-12所示。

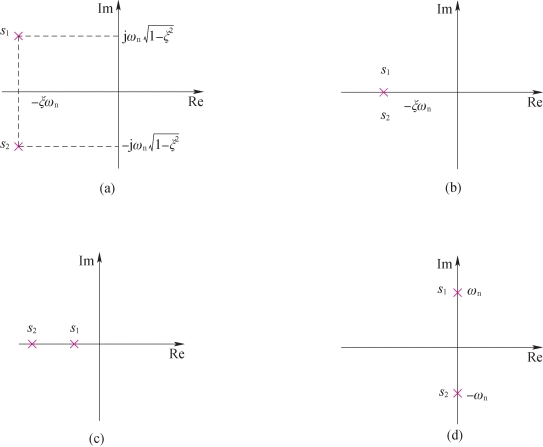
图3-12　二阶系统极点分布

（a）0＜ξ＜1；（b）ξ=1；（c）ξ＞1；（d）ξ=0

（1）当0＜ξ＜1时，二阶系统称为欠阻尼系统，其特征方程的根是一对共轭复根，如图3-12（a）所示；即极点是一对共轭复数极点

令，称为有阻尼振荡角频率，则有

（2）当ξ=1时，二阶系统称为临界阻尼系统，其特征方程的根是两个相等的负实根，如图3-12（b）所示；即具有两个相等的负实数极点

（3）当ξ＞1时，二阶系统称为过阻尼系统，其特征方程的根是两个不相等的负实根，如图3-12（c）所示；即具有两个不相等的负实数极点

（4）当ξ=0时，二阶系统称为零阻尼系统，其特征方程的根是一对共轭虚根，如图3-12（d）所示；即具有一对共轭虚数极点

（5）当ξ＜0时，二阶系统称为负阻尼系统，此时系统不稳定。