常见的输入信号类型

时域分析法分析控制系统的动态性能是从时间响应的角度入手进行系统分析。从微分方程理论可知，系统的时间响应不仅取决于系统本身的结构参数，而且与系统的初始状态和施加于系统的输入信号的形式有关。例如：RC网络，电容上有没有初始电压，输入信号是直流还是交流，其输出响应大不相同。另外，大部分控制系统的实际输入信号不可预知，且具有随机性。例如：在机电设备的运行过程中，电网电压的变化、设备负载的波动以及环境因素的干扰等都无法预先知道，因此，用简单、确定的数学表达式表示输入信号几乎不可能。

为了比较控制系统性能优劣，揭示其内部特征，需要有一个对各种控制系统的性能进行比较的基础，通常对系统的初始状态和输入信号做一些典型化处理。

1.典型初始状态

由式（3-8）可知，系统的储能元件初始状态不为0时，时间响应由零输入响应和零状态响应组成。其中，零输入响应由初始状态决定，并且仅对响应项的系数有影响，即仅对响应曲线的形状有影响，而不会影响响应的性质。故为分析方便，规定控制系统初始状态均为零状态，零输入响应为0。也就是说，在输入信号加于系统的瞬间（t=0）之前，系统是相对静止的，即被控量及其各阶导数相对于平衡工作点的增量为0。这种处理对大多数控制系统而言是符合实际情况的。

2.典型输入信号

由于实际控制系统输入信号的复杂性，为了便于分析和计算，预先规定一些典型实验信号作为系统的输入信号，不仅简化了数学处理方法，而且还可以推知其他更为复杂情况下的形态的性能。在用实验法测取和分析系统的动态性能时，典型输入信号也是经常采用的测试信号。实际应用中究竟采用哪一种典型信号，取决于系统常见的工作状态和数学分析的方便程度。例如：为了使随动系统对位置、速度和加速度等输入信号具有良好的跟随性，给定作用分别取阶跃、斜坡和加速度信号；对于过程控制中的定值控制系统，为了使系统具有良好的抗干扰能力，通常选取阶跃信号作为输入信号。这是因为阶跃干扰被认为是最不利或者说最严重的的情况，若系统在这种输入作用下，其稳态响应和瞬态响应能够满足控制系统的要求，那么在实际干扰作用下的时间响应将能满足工艺过程所提的要求。

常见的典型输入信号如图3-2所示。

下面介绍常用典型输入信号的数学表达形式。

（1）阶跃信号，是指输入量突变为数值为常值的信号，如图3-2（a）所示。

其数学表达式为

其中a为常数，当a=1时，该信号称为单位阶跃信号，记为1（t）。

其拉氏变换式为

阶跃信号是评价系统动态性能常用的一种典型信号。阶跃信号可用来模拟物理量的突变，如：电机负载的突然加重或释放、指令的突然转换、继电器接点的闭合等。

图3-2　常见的典型输入信号

（a）阶跃信号；（b）斜坡信号；（c）加速度信号；（d）脉冲信号；（e）正弦信号

（2）斜坡信号，是指输入变量是等速度变化的信号，如图3-2（b）所示。

其数学表达式为

其中a为常数，当a=1时，该函数称为单位斜坡信号，记为t·1（t）。

其拉氏变换为(www.xing528.com)

斜坡信号也称为等速度信号，单位斜坡信号也称为单位速度信号。它是阶跃信号对时间的积分。当积分器的输入端施加恒定电压时，其输出电压信号就是斜坡信号；又如车床卡盘以匀速旋转时，则主拖动系统发出的角位移信号就是斜坡信号。

（3）加速度信号，是指输入变量是等加速度变化的信号，又称为抛物线信号，如图3-2（c）所示。

其数学表达式为

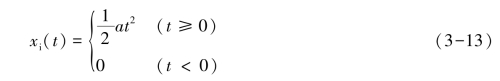
其中a为常数，当a=1时，该函数称为单位加速度信号，记为。等加速度信号等于斜坡信号对时间的积分，而它对时间的导数就是斜坡信号。

其拉氏变换为

单位速度信号和单位加速度信号在随动系统中是常见的。特别是在研究随动系统稳态精度时，经常利用这类信号进行分析。

（4）脉冲信号。脉冲信号的数学表达式为

其中a为常数，因此当0＜t＜h时该函数为无穷大。

如图3-2（d）所示，其脉冲高度为a/h，是无穷大；持续时间为h，是无穷小；脉冲面积为a。因此，通常脉冲强度是以其面积a衡量的。当面积a=1时，脉冲函数称为单位脉冲函数，又称δ函数，其数学表达式为

其拉氏变换为

理想单位脉冲信号δ（t）在现实中是不存在的，只有数学上的意义，但它却是一个重要的数学工具。

（5）正弦信号。正弦信号如图3-2（e）所示。

其数学表达式为

其拉氏变换为