基本环节传递函数优化

系统的传递函数往往是高阶的，但不管它们的阶次有多高，均可化为零阶、一阶、二阶的一些典型环节（如比例环节、惯性环节、微分环节、积分环节、振荡环节）和延时环节。熟悉这些环节的传递函数，对于了解与研究系统会带来很大的方便。下面介绍这些环节的传递函数及其推导。

1.比例环节（放大环节）

凡输出量与输入量成正比，输出量不失真也不延迟且按比例地反映输入量的环节称为比例环节。其动力学方程为

式中，xo（t）为输出量；xi（t）为输入量；K为环节的放大系数或增益。其传递函数为

理想的电子放大器、无侧隙的齿轮传动机构、质量高的测速发电机和伺服放大器等都可以认为是比例环节。

【例2-12】图2-10所示为齿轮传动副，xi、xo分别为输入、输出轴的转速，z1、z2为齿轮齿数。

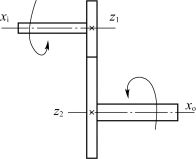
图2-10　齿轮传动副

解　如果传动副无传动间隙、刚性无穷大，那么一旦有了输入量xi，就会产生输出量xo，且

此方程经拉普拉斯变换后得传递函数

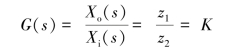
式中，K为齿轮传动比，也就是齿轮传动副的放大系数或增益。

2.惯性环节

凡动力学方程为一阶微分方程

形式的环节为惯性环节。其传递函数为

式中，K为放大系数；T为惯性环节的时间常数。

【例2-13】分析图2-11所示的阻尼-弹簧系统的传递函数。

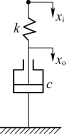
图2-11　阻尼-弹簧系统

解　该系统的动力学方程为

经拉普拉斯变换后，有

故传递函数为

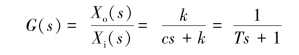
式中，T=c/k，称为惯性环节的时间常数。

因惯性环节含有弹性储能元件k和阻性耗能元件c，其输出落后于输入。与比例环节相比，此环节具有“惯性”，在阶跃输入时，输出需经历一段时间才能接近所要求的阶跃输出值。惯性大小由时间常数T衡量。

【例2-14】分析图2-12所示阻容电路的传递函数，ui为输入电压，uo为输出电压，i为电流，R为电阻，C为电容。

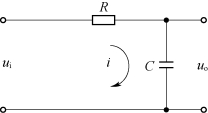
图2-12　阻容电路

解　该电路的动力学方程为

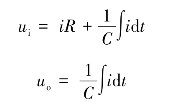
由上可知

故

传递函数为

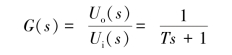
式中，T=CR为惯性环节的时间常数。

本系统之所以成为惯性环节，是由于含有容性储能元件C和阻性耗能元件R。

上述两例说明，在一定条件下，不同物理系统可以具有相同的传递函数。

3.微分环节

凡具有输出正比于输入的微分，即具有

的环节称为微分环节，显然，其传递函数为

式中，T为微分环节的时间常数。

【例2-15】测速发电机是用于测量角速度并将它转换成电压量的装置。在控制系统中常用的有直流和交流测速发电机，如图2-13所示。图2-13（a）是永磁式直流测速发电机的原理示意图，图2-13（b）是交流测速发电机的原理示意图。试求两种发电机的传递函数。

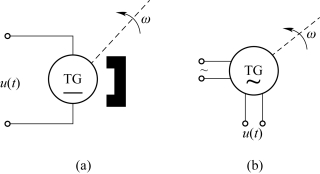
图2-13　测速发电机

（a）永磁式直流测速发电机；（b）交流测速发电机

解　由图2-13（a）可以看出，测速发电机的转子与待测量的轴相连接，在电枢两端输出与转子角速度成正比的直流电压，即

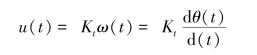
式中，θ（t）是转子角位移；ω（t）是转子角速度；Kt是测速发电机输出斜率，表示单位角速度的输出电压。

该系统传递函数为

由图2-13（b）可以看出，交流测速发电机有两个互相垂直放置的线圈，其中一个是激磁绕组，接入一定频率的正弦额定电压，另一个是输出绕组。当转子旋转时，输出绕组产生与转子角速度成比例的交流电压u（t），其频率与激磁电压频率相同，其传递函数亦为式（2-89），与直流测速发电机相同。

微分环节对系统的控制作用如下。

1）预测输出

如对比例环节输入-斜坡函数r（t）=t，则当比例系数KP=1时，此环节在时域中的输出xo（t）即为45°斜线，如图2-14所示；若对此比例环节再并联一微分环节KPTs，则微分环节预测输出如图2-15（a）所示。此时传递函数为

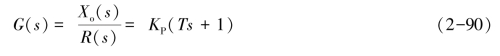
即并联了微分环节后，在相同时刻所增加的输出

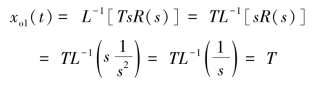
如图2-15（a）所示，系统在每一时刻的输出都增加了T，在原输出为45°斜线时，新输出也是45°斜线，它可以看成原输出向左平移T，即原输出在t2时刻才有的xo（t2），新输出在t1时刻就已达到（即b点的输出等于c点的输出）。

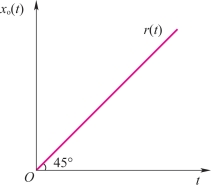
图2-14　KP=1时比例环节的输出

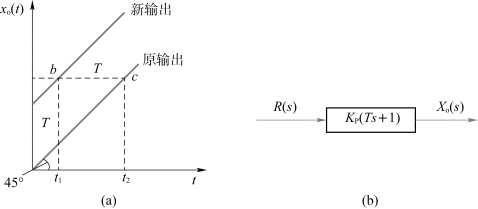
图2-15　微分环节预测输出

（a）预测输出；（b）传递函数

微分环节的输出是输入的导数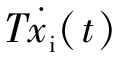，它反映了输入的变化趋势，所以也等于对系统的有关输入变化趋势进行预测，由于微分环节使输出提前，预测了输入的情况，因而有可能对系统提前施加校正作用，提高系统的灵敏度。

2）增加系统的阻尼(www.xing528.com)

如图2-16（a）所示，系统的传递函数为

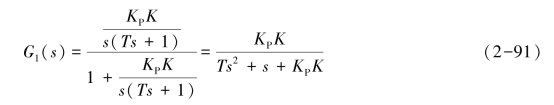
对系统的比例环节KP并联微分环节KPTds，如图2-16（b）所示，化简后，其传递函数为

比较上述两式可知，G1（s）与G2（s）均为二阶系统的传递函数，其分母中第二项s前的系数与阻尼有关，因为1+KPKTd＞1，所以采用微分环节后，系统的阻尼增加。

图2-16　微分环节增加系统阻尼

（a）比例环节；（b）并联微分环节

4.积分环节

凡具有输出正比于输入对时间的积分，即具有

的环节称为积分环节，其传递函数为

式中，T为积分环节的时间常数。

【例2-16】图2-17所示为齿轮-齿条传动机构，试求其传递函数。

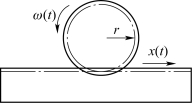
图2-17　齿轮-齿条传动机构

解　取齿轮的转速ω（t）为输入，齿条的位移x（t）为输出，其数学模型为

式中，r为齿轮节圆半径。

对式（2-95）取拉氏变换，得其传递函数为

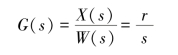
积分环节的一个显著特点是输出量取决于输入量对时间的积累过程，输入量作用一段时间后，即使输入量变为0，输出量仍将保持在已达到的数值，故有记忆功能；另一个特点是有明显的滞后作用。积分环节的性质如图2-18所示，从图中可以看出，输入量为常值A时

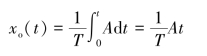
xo（t）是一条斜线，输出量需经过时间T的滞后，才能达到输入量xi（t）在t=0时的数值。

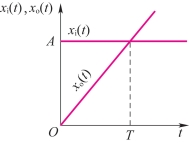
图2-18　积分环节的性质

5.振荡环节

振荡环节是二阶环节，其传递函数为

或写成

式中，ωn为无阻尼固有频率；T为振荡环节的时间常数，T=1/ωn；ξ为阻尼比。

【例2-17】图2-19所示为一个做旋转运动的惯量-阻尼-弹簧系统，在转动惯量为J的转子上带有叶片与弹簧，其弹簧扭转刚度与黏性阻尼系数分别为k与c。若在外部施加一扭矩M作为输入，以转子转角θ作为输出，求系统的传递函数。

图2-19　惯量-阻尼-弹簧系统

解　系统动力学方程为

故得传递函数为

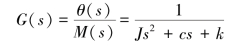
或写成

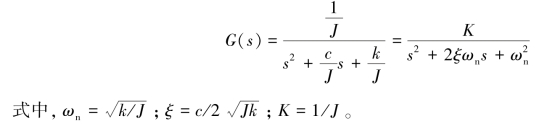
【例2-18】图2-20所示为R-L-C电路，ui为输入电压，uo为输出电压。求系统的传递函数。

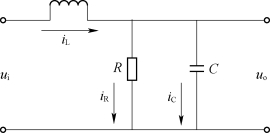
图2-20　R-L-C电路

解　电路的动力学方程为

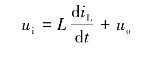
而

将后两式代入动力学方程，得

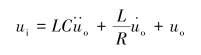
两边取拉氏变换并整理得传递函数为

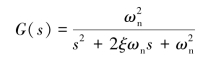
式中，。由电学可知，ωn为电路的固有振荡频率，ξ为电路的阻尼比。显然，这与质量-阻尼-弹簧的单自由度机械系统的情况相似。

上述两例中的阻尼比ξ满足0≤ξ＜1时，二阶环节才为振荡环节。

6.延时环节

延时环节是输出滞后输入但不失真地反映输入的环节。注意：延时环节一般与其他环节同时共存，而不单独存在。

延时环节的输入xi（t）与输出xo（t）之间有如下关系

式中，τ为延迟时间。

延时环节是线性环节，因为它符合叠加原理。设系统的作用相当于算子A，即xi（t）通过算子A的作用而变为xo（t），则

对延时环节而言，有

从而有

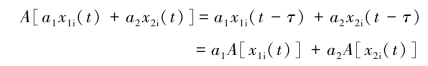
这表明算子A是线性的，即延时环节是线性环节，符合叠加原理。

根据式（2-98），可得延时环节的传递函数为

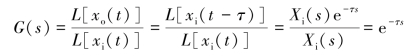
延时环节与惯性环节不同，惯性环节的输出需要延迟一段时间才接近于所要求的输出量，但从输入开始时刻起就已有了输出。延时环节在输入开始之初的时间τ内并无输出，在τ后，输出就完全等于从一开始起的输入，且不再有其他滞后过程；简言之，其输出等于输入，只是在时间上延时了一段时间间隔τ。

这种纯时间延迟或传输滞后现象，可由图2-21所示的带钢轧制厚度检测环节看出。带钢在A点轧出时，产生厚度偏差，但到达B点时才被测厚仪检测到。延迟时间为

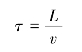
式中，L为测厚仪与机架的距离；v为带钢速度。

因而，轧辊处带钢厚度与检测点厚度之间的传递函数就是一个延时环节。

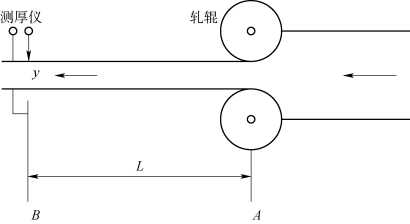
图2-21　带钢轧制厚度检测环节