系统非线性微分方程的线性化方法

严格地讲，系统或元件都存在不同程度的非线性。由于目前非线性系统的理论和分析方法还不成熟，故往往只能在一定条件下将描述非线性系统的非线性微分方程线性化，用线性系统理论对其进行分析和综合。

系统通常都有一个预定工作点，即系统处于某一平衡位置。对于自动调节系统或随动系统，只要系统的工作状态稍一偏离此平衡位置，整个系统就会立即做出反应，并力图恢复原来的平衡位置。假定变量对某一工作状态的偏离很小，设系统的输入量为x，输出量为y。x和y的关系为

如果系统在平衡位置处输入量和输出量的值分别为，，那么式（2-26）可以在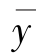（，）点附近展开成泰勒级数此，式（2-27）可写成

式中，…均在x=点进行计算。因为假定x-很小，可以忽略x-的高阶项。因

式（2-28）说明（y-）与（x-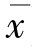）成正比。式（2-28）就是由式（2-26）定义的非线性系统的线性化数学模型。

若输出量y是两个输入量x1和x2的函数，即

为了得到这一非线性系统的近似线性关系，将式（2-29）在平衡工作点，附近展开成泰勒级数：

式中，偏导数都在x1=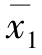，x2=上进行计算。在平衡工作点附近，高阶项可以忽略不计。于是在平衡工作点附近，这一非线性系统的线性化数学模型可以写成

【例2-7】图2-8所示为一个阀控缸系统。其工作原理是当阀芯右移时，高压油进入液压缸左腔，这时活塞推动负载右移；反之，当阀芯左移时，活塞推动负载左移。试建立该系统的线性化流量方程及系统的微分方程。

解　由图2-8可知，x为滑阀的位移，y为活塞位移输出。设q为进入动力油缸的油液流量（负载流量），Δp=p1-p2为动力活塞两侧的压力差，A为活塞有效面积，m为负载质量，c为黏性阻尼系数，则阀控缸系统的动力学方程为

(www.xing528.com)

图2-8　阀控缸系统

若阀口结构完全相同且对称，不考虑阀和缸的泄漏时，流入流出液压缸的流量相同，其连续性方程为

根据流体流经伺服阀的微小开口的流量特性，负载流量q，x和Δp之间的关系为非线性关系，可表示为

把这一非线性方程在预定工作点，和附近线性化，可得

对伺服阀来说，由于负载压力p增大，负载流量q总是减小的，因而本身总是负值。为定义流量-压力系数为正，故kc前冠以负号。

若预定工作点选在阀的零位，即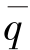=0，=0，则线性化流量方程可写为

图2-9所示为q，x和Δp之间的线性关系，图中各直线是以x为参变量的阀控缸系统的线性化特性曲线。

将式（2-36）、式（2-33）代入式（2-32），消去中间变量q及Δp后，得系统的阀开口与输出关系的线性化微分方程为

若考虑油的压缩性，则上式将为三阶方程，考虑油液泄漏时，阶数将不受影响，只是方程更精确一些。

图2-9　阀控缸系统的线性化特性曲线