电气系统是机械控制系统的重要组成部分。在电气系统中,通过电阻R、电感L、电容C三种线性无源元件的组合,可以构成各种复杂的电网络系统。电感是一种储存磁能的元件,电容是储存电能的元件;电阻不储存能量,是一种耗能元件,将电能转换成热能耗散掉。
电气系统所遵循的基本定律是基尔霍夫电流定律和电压定律。基尔霍夫电流定律表明,流入节点的电流之和等于流出同一节点的电流之和;而基尔霍夫电压定律表明,在任意瞬间,在电路中沿任意环路的电压的代数和等于0。通过应用一种或同时应用两种基尔霍夫定律,就可以得到电路系统的数学模型。
【例2-4】如图2-5所示的无源电路系统中,ui(t)为输入电压,uo(t)为输出电压,试建立其微分方程。
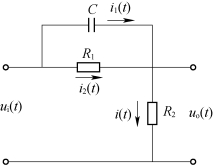
图2-5 无源电路系统
解 根据欧姆定律和基尔霍夫定律,有
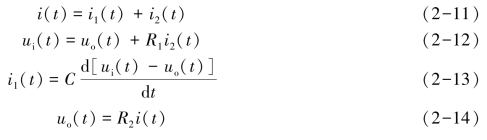
由式(2-12)得

由式(2-14)得
![]()
将式(2-13)、式(2-15)和式(2-16)代入式(2-11),得
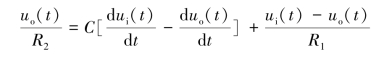
即
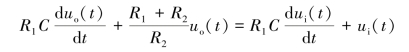
【例2-5】如图2-6所示的有源电路系统中,ui(t)为输入电压,uo(t)为输出电压,K0为运算放大器开环放大倍数。试建立其微分方程。
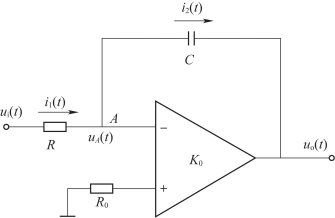
图2-6 有源电路系统
解 设运算放大器的反相输入端为A点。根据运算放大器输入端电压关系v+≈v-,又同相输入端接地,即v+=0,可得
![]()
因为一般运算放大器的输入阻抗很高,所以
![]()
据此可列出
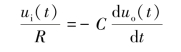
即(https://www.xing528.com)
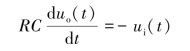
【例2-6】如图2-7所示的电枢控制式直流电动机系统中,ei(t)为电动机电枢输入电压,θo(t)为电动机输出转角,Ra为电枢绕组的电阻,La为电枢绕组的电感,ia(t)为流过电枢绕组的电流,em(t)为电动机感应电势,T(t)为电动机转矩,J为电动机及负载折合到电动机轴上的转动惯量,c为电动机及负载折合到电动机轴上的黏性阻尼系数。试建立其微分方程。
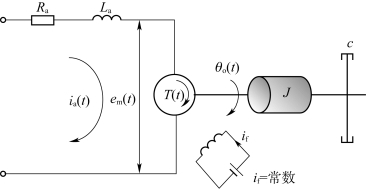
图2-7 电枢控制式直流电动机系统
解 根据基尔霍夫定律,有
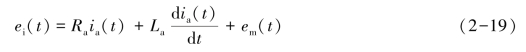
根据磁场对载流线圈的作用定律,有
![]()
式中,KT为电动机转矩常数。
根据电磁感应定律,有

式中,Ke为反电动势常数。
根据牛顿第二定律,有
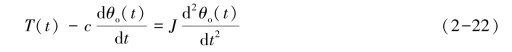
将式(2-20)代入式(2-22),得
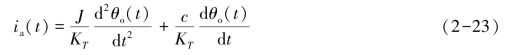
将式(2-21)、式(2-23)代入式(2-19),得
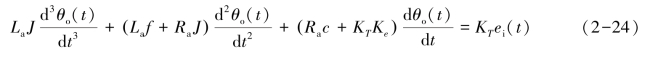
在工程应用中,由于电枢电感La较小,通常忽略不计,因而系统微分方程可简化为
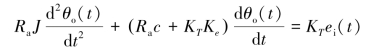
当电枢电感La和电阻Ra均较小,可以忽略时,系统微分方程可进一步简化为
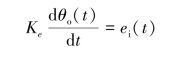
从以上例子可以看出,线性系统的微分方程具有类似的形式。更一般化地,设线性定常系统的输入量为xi(t),输出量为xo(t),则描述系统输入量、输出量动态关系的微分方程为
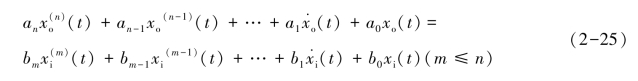
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




