在机械系统中,某些部件具有较大的惯性和刚度,而另一些部件则惯性较小、柔性较大。在使用集中参数法时,可将前一类部件的弹性忽略,将其视为质量;而把后一类部件的惯性忽略,将其视为无质量的弹簧。这样对机械系统而言,只要通过一定的简化,大多可抽象为质量-弹簧-阻尼系统及其综合。
在抽象为质量-弹簧-阻尼系统的机械系统中,牛顿第二定律是机械系统所必须遵循的基本定律,通过牛顿第二定律将机械系统中的运动(位移、速度和加速度)与力联系起来,建立机械系统的动力学方程,即机械系统微分方程。
下面举例说明机械系统微分方程的列写方法。
【例2-1】弹簧-质量-阻尼系统如图2-2所示。设系统的输入量为外力x,输出量为质量的位移y,试写出系统的微分方程。
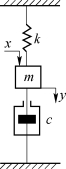
图2-2 弹簧-质量-阻尼系统
解 在这个系统中,m表示质量,c表示黏性阻尼系数,k表示弹簧刚度。对于线性系统而言,弹簧力方向与运动方向相反,大小与位移成比例;阻尼力方向与运动方向相反,大小与运动速度成比例。
根据牛顿第二定律,可得

或

式(2-3)即为描述该机械系统输入量、输出量动态关系的微分方程。
【例2-2】图2-3所示为由两个质量和弹簧串联而成的二自由度振动系统,输入量为外力f(t),m1的位移为y1(t),m2的位移为y2(t)。试列写以f(t)为输入量,y1(t)为输出量时系统的微分方程。

图2-3 二自由度振动系统
解 当m2与k2不存在时,图2-3所示系统为单自由度系统,其输入量与输出量之间的动力学方程为
![]()
当m2与k2连接到m1与k1上时,便对m1和k1产生了负载效应,此时,系统变成二自由度系统,其动力学方程为(https://www.xing528.com)
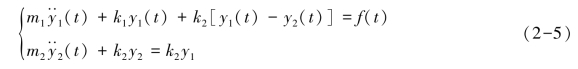
从以上两式中消去y2(t),则得到以f(t)为输入量,y1(t)为输出量的系统动力学方程为
![]()
显然,由式(2-6)求解出y1(t)与式(2-4)求解出y1(t)的结果不同。
例2-2说明,对于两个物理元件组成的系统,若其中一个元件的存在,使另一个元件在相同输入下的输出受到影响,相当于前者对后者施加了负载,这一影响称为负载效应,或称耦合。对于这样的系统,在列写它们各自的动力学方程时,必须考虑元件间的负载效应,才能求得整个系统正确的动力学方程。
【例2-3】图2-4所示的齿轮传动系统,Mi(t)是输入转矩,M是输出轴上所带负载的阻转矩,J1、c1、J2、c2分别为主动轴和从动轴的转动惯量和黏性阻尼系数,减速器的传动比为i。如果以Mi(t)为输入量,以θ1(t)为输出量,试列写出系统的运动方程。

图2-4 齿轮传动系统
解 M1(t)为从动轴作用于主动轴上的转矩,M2(t)为主动轴作用于从动轴上的转矩,对于主动轴和从动轴,分别根据转矩平衡方程列写系统方程
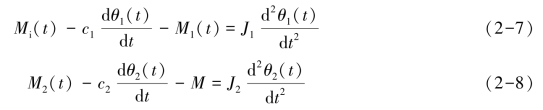
齿轮传动系功率平衡方程为
![]()
传动比

将式(2-8)、式(2-9)及式(2-10)代入式(2-7),消去中间变量M1(t)、M2(t)、θ2(t),得
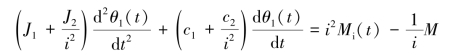
如果齿轮系传动比足够大,则后级齿轮及负载的影响便可不予考虑。这时微分方程可简化为线性方程
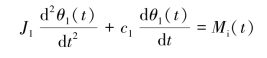
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




