单一参数元件的正弦交流电路

2.3　单一参数元件正弦交流电路

任何电路都是由电源和一个个单一元件所组成，其单一元件就是指电阻R、电感L、电容C。

2.3.1　纯电阻电路

若流过一个电阻R上的正弦交流电流为i，则将在电阻两端产生电压u。为了便于分析，取电阻R上电流、电压的参考方向为关联参考方向，如图2-10（a）所示，假设

i=I_msinωt

则由欧姆定律得

u=iR=I_mRsinωt=U_msinωt

比较上述两式，可知电压与电流是同频率的正弦量。

1.电压与电流的关系

（1）电压与电流相位相同，其波形和相位图如图2-10（b）和图2-10（c）所示。

（2）电压与电流的最大值、有效值成正比。

U_m=I_mR；U=IR

（3）电压与电流的相量表达式为

式（2-23）包含了相位和有效值关系。

2.功率关系　知道了电阻上电压和电流的相互关系及变化规律后，便可进一步研究电路中的功率问题。在任意瞬间，电阻上的瞬时功率即为电压、电流瞬时值的乘积，一般用小写字母p表示，即

p=ui=U_mI_msin²ωt

=2UIsin²ωt=UI（1-cos2ωt）

由式（2-24）可见，电阻R上的瞬时功率是变化的，其变化的波形见图2-10（d）。由于在关联参考方向下，电阻上电压与电流同相位，它们同时为正，同时为负，因此瞬时功率p总大于零，即p≥0。这表明电阻总是从电源吸取电功率，把电能转换成热能，所以称电阻为耗能元件。

由于瞬时功率是变化的，不便应用。通常所说的功率是指瞬时功率在一周内的平均值，称为平均功率或有功功率，用大写字母P表示，即

可见，平均功率在形式上和直流电阻电路的计算式相同。式（2-25）中的电压、电流都是指有效值。由于平均功率是电路中实际消耗的电功率，所以又叫有功功率，简称有功，其单位为瓦特（W）。

【例2-6】将一个10Ω电阻接在u=311sin（ω+30°）V电源上，求电路中的电流i和有功功率P。

解：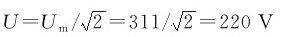

I=U/R=220/10=22A

P=UI=220×22=4840W

2.3.2　纯电感电路

在一个只具有电感L（忽略其内阻）的线圈上，加一正弦交流电压u，则线圈中将有电流i通过，并将产生自感电动势e_L。若电感线圈上的电压及电流为关联参考方向，且与电动势e_L同方向，如图2-11（a）所示，电感线圈上瞬时值表示的伏安特性方程为

设电流为

i=I_msinωt

则

=U_msin（ω+90°）

由此可见，电感上的电压、电流是同频率的正弦量。

1.电压与电流的关系

（1）在相位上，电感线圈的电压超前于电流90°。其波形图与相量图如图2-11（b）和图2-11（c）所示。

（2）电压与电流有效值成正比，即

U=IωL=IX_L或U_m=I_mX_L

式（2-26）中，X_L=ωL=2πfL，称为比例常数。它具有限制电流的作用，称为电感电抗，简称感抗。当L的单位为亨（H），f的单位为赫兹（Hz），ω的单位为弧度/秒（rad/s）时，X_L的单位为欧姆（Ω）。对于直流电路，稳态运行的f=0，则X_L=0，相当于电感短路。

（3）用相量的形式表示为

2.功率关系　将上文的电压u与电流i代入瞬时功率的表达式中，即得电感元件输入的瞬时功率

p=ui=U_mI_msinωtsin（ω+90°）

=2UIsinωtcosωt=UIsin2ωt

它是一个角频率为2ω的正弦变化量，其波形如图2-11（d）所示。从图中看到，瞬时功率有正有负。p为正值时，表示电感把从电源吸收的电能转换成磁场能；p为负值时，表示电感把磁场能转换为电能送还电源。这是一个可逆的能量转换过程，而且纯电感从电源取用的能量一定等于归还给电源的能量，就是说电感不消耗有功功率，这一点也可从平均功率看出。

虽然电感元件不消耗有功能量，但与电源之间有能量的交换。为了衡量电感元件与电路交换能量的多少，工程上用电感元件瞬时功率的最大值来表示。电源与电感之间交换功率的最大值称为无功功率，用以区别有功功率，并以Q_L表示。

无功功率的单位为乏（var）或千乏（kvar）。(www.xing528.com)

需要说明的是：不要把“无功”功率理解为“无用”功率。实际上无功功率在工程上占有重要地位，例如电磁铁、变压器、电动机等一些具有电感性质的设备，没有磁场是不能工作的，而磁场能量是由电源提供的，电源需要向设备提供一定规模的能量与之进行交换才能保证设备的正常运行。

【例2-7】一个电感L=25.4mH的线圈（忽略线圈电阻）接在交流电压u=311sin（314t-60°）V的电源上：

（1）求感抗X_L、电流i、无功功率Q_L；

（2）当电源频率增大10倍（f′=10f），其他参数不变时，再求X_L、i和Q_L。

解：（1）ω=314rad/s,f=50Hz，有

X_L=2πfL=314×25.4×10^-3=8Ω

Q_L=UI=220×27.5=6050var

（2）f′=10f=500Hz，ω=3140rad/s

X_L=10×8=80Ω

Q_L=UI=220×2.75=605var

2.3.3　纯电容电路

在一个只有电容元件的电路中，加一正弦交流电压u，则将产生一电流i。若按惯例取u与i为关联参考方向，如图2-12（a）所示，可得电容C的瞬时值伏安特性方程为

设电压为

u=U_msinωt

代入式（2-27）可得电容电流为

=Imsin（ω+90°）

显然，电容上的电压、电流也是同频率的正弦量，由此可得电容上的电压、电流关系。

1.电压与电流的关系

（1）在相位上，电容电流超前于电容电压90°，其波形与相量图如图2-12（b）与图2-12（c）所示。

（2）电容电流有效值正比于电容电压有效值。即

I=ωCU

或

式（2-28）中比例常数XC=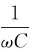=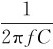，说明它也有限制电流的作用，并称其为电容电抗，简称容抗。若C的单位用法拉（F），f的单位用赫兹（Hz），ω的单位用弧度/秒（rad/s），X_L的单位为欧姆（Ω）。

在直流电路中，稳态运行时，f=0，X_L为无穷大，相当于电容开路，所以说电容有隔断直流的作用。当频率非常高时，X_C将很小，故电容在高频电子线路时，一般近似为短路。

（3）用相量表示时，则有

2.功率关系电容元件输入的瞬时功率p为电压u与电流i的乘积，即

p=ui=U_mI_msinωtsin（ω+90°）

=2UIsinωtcosωt

=UIsin2ωt

它是一个角频率为2ω的正弦变化量，其波形如图2-12（d）所示。从图中看到瞬时功率仍有正负。p为正值时，表示电容把电源的电能转换成电场能，即电容在充电；p为负值时，表示电容把电场能变为电能送回电源。这仍是一种可逆的能量转换过程。

在电容元件的电路中，电容上的平均功率

这说明电容元件是不消耗有功能量的。由于电压、电流的有效值不为零，因此，电源与电容之间交换功率的最大值也称为无功功率，用Q_C表示，以区别有功功率。即

Q_C=UI=I²X_C

Q_C与Q_L的单位相同。

【例】一个电容C的电容器，接在交流电压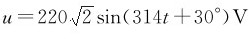的电源上：

（1）求容抗X_L、电流i和无功功率Q_C；

（2）当f=5000Hz时，其他参数不变，再求容抗XL、电流i和无功功率QC。

解：（1）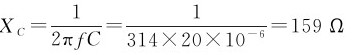

Q_C=UI=220×1.38=303.6var

（2）当f=5000Hz（增大100倍），

Q_C=UI=220×138=30360var=30.36kvar