正弦量的相量表示

2.2　正弦量的相量表示

正弦量随时间变化的情况可以通过波形图或三角函数表达式来描述，这两种表示正弦量的方法比较直观，但是进行运算并不方便，因为电路内如正弦量之间一般情况下都具有相位差。例如，两个同频率但初相位不同的电流i₁、i₂作求和计算时，和电流

i=i₁+i₂=I_m1sin（ωt+ψ_i1）+I_m2sin（ωt+ψ_i2）

因为ψ_i1≠ψ_i2，所以求和电流i（即要得到它的最大值I_m、初相位ψ_i）需要通过三角函数关系式进行运算或利用电流i₁、i₂的波形图逐点相加才能求得，显然这是很不方便的。因此需要有一种简便而实用的表示正弦量的方法，以简化交流电路的分析与计算，这就是通常使用的正弦量的相量表示法。应用相量法可以把交流电路中按正弦规律变化的电压、电流变换成相量图或相量（复数）形式，使正弦量的运算变换为几何或复数运算。为了理解和掌握相量法，必须对复数的运算有所了解，因此这里简要介绍一些有关复数的基本知识。

2.2.1　复数的表示形式

设A为复数，一般可表示为

A=a+jb

式（2-9）称为复数的代数式，其中a是复数的实部，b是复数的虚部，j=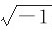是虚数单位（或称算子）。

复数还可以由实轴与虚轴组成的复平面上的矢量（有向线段）表示。在图2-6中，复数A所对应的矢量为r，矢量的长度r称为复数A的模，矢量与实轴正方向的夹角ψ称为复数的辐角，由此可得复数的另一种表示式，即

A=r∠ψ

式（2-10）称为复数的极坐标式。由图2-6得

又因为

a=rcosψ

b=rsinψ

所以

A=rcosψ+jrsinψ

式（2-12）称为复数的三角式。

根据欧拉公式

可得

cosψ+jsinψ=e^jψ

则式（2-12）可写为

A=re^jψ

式（2-13）称为复数的指数式。

综上所述，同一复数及其所对应的矢量可以用代数式、三角式和指数式表示，即

A=a+jb=rcosψ+jrsinψ=re^jψ

其目的就是为了便于复数的数学运算。

【例2-2】化下列复数为指数式：（1）A=5+j5；（2）A=4-j3；（3）A=-j10。

解：用A和ψ分别表示复数A的模和辐角，由式（2-11）可得

（1），有

则

（2）

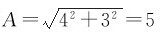
则

这里应注意，求辐角时，要把a和b的符号分别保留在分母和分子中，以便正确判断ψ的大小。

（3）由A=-j10可知，该复数应在复平面虚轴的负方向上，模为10，辐角为-90°，故得

【例2-3】化下列复数为三角函数式和代数式：（1）；（2）；（3）。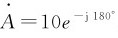

解：由式（2-12）可得(www.xing528.com)

2.2.2　正弦量的相量表示法

设有一正弦电流i=I_msin（ω+ψ），图2-7所示的复平面上有一旋转矢量，设该矢量的长度代表正弦电流的最大值I_m，它的初始位置与实轴正方向之间的夹角等于正弦电流的初相位ψ，并以角速度ω（正弦电流的角频率）作逆时针方向旋转。可见这个旋转矢量具有正弦量的3个特征量。正弦量在某一时刻的瞬时值可以用这个旋转矢量在该时刻纵轴上投影高度表示。例如，在t=0时，i（0）=I_msinψ；在t=t₁时，i（t₁）=I_msin（ω₁+ψ），因此可用旋转矢量来表示正弦量，图2-7也给出了旋转矢量所对应的电流的波形。

如前所述，复平面上的矢量可用复数表示。既然可以用矢量表示正弦量，那么复数也可以表示正弦量。在交流电路中，当外加正弦交流电源的频率f一定时，电路中各部分的电压和电流的频率也都与电源的频率相同，所以在分析过程中可以把角频率这一特征量作为已知量。因此，同频率的正弦电量在进行运算时，可不考虑矢量在复平面中的旋转问题，即不必考虑旋转因子e^jωt，而只要用固定矢量表示正弦量的最大值和初相位就可以了。为了与一般复数相区别，通常把表示正弦电量的复数称为相量，用大写英文字母加上点来表示，并将表示正弦交流电最大值和初相位的相量称为最大值相量。如电流i=I_msin（ω+ψ）的最大值相量为

有时为计算方便，也用有效值相量来等价的表示正弦交流电。有效值相量的模就是正弦电量的有效值，辐角也是正弦电量的初相位。交流电压和电流最大值相量和有效值相量的关系是

正弦量用相量表示以后，原来是三角函数的运算就变换成相量运算，这种利用相量分析交流电路的方法叫相量法。相量法给正弦电量的运算带来很大的方便，它是分析正弦交流电路的主要工具。

在复平面中按照一定的大小和相位关系画出的一组相量图形称为相量图。借助相量图常常可以使相量之间的关系和物理概念更加清楚，所以正确画出相量图对于分析正弦交流电路是十分重要的。

下面通过例题进一步说明正弦量的相量表示法及画相量图的方法。

【例2-4】若电流i₁=5sin（314t+60°）A,i₂=10cos（314t+60°）A,i₃=-4sin（314t+60°）A。试写出这3个电流的相量，并画出相量图。

解：由式（2-14）得i₁=5sin（314t+60°）A的最大值相量为

有效值相量为

i₂=10cos（314t+60°）=10sin（314t+150°）A的最大值相量为

有效值相量为

i₃=-4sin（314t+60°）=4sin（314t+60°+180°）

=4sin（314t+240°）=4sin（314t-120°）A的最大值相量为

有效值相量为

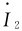、、三个电流的相量图如图2-8（a）所示。

在画相量图时也可以不画出复平面的坐标轴。若几个相量画在同一相量图上，可以一个相量作为参考相量，画在与实轴正方向一致的水平位置，而其他相量则可根据与参考相量间的相位差画出，如图2-8（b）所示。图中是以作为参考相量画出的相量图。

【例2-5】已知两正弦电流i₁=8sin（ω+45°）A和i₂=6sin（ω+135°）A，试求：i=i₁+i₂，并画出各电流的相量图。

解：首先用有效值相量表示两电流

再求两电流和的相量

最后根据求得i的有效值相量，写出该电流的瞬时值表达式

=10sin（ω+81.86°）A

相量图如图2-9所示。

通过以上例题可以看出：

（1）相量法的实质就是将同频率的正弦量变换为相量（复数），然后进行相量运算，求出待求量的相量，最后再把它变换为正弦量的瞬时值表达式。因此，只有正弦量才能用相量表示，非正弦量不能用相量表示。

（2）相量只是表示正弦量的有效值（或最大值）和初相位的复数，不要把正弦量的相量误认为就是正弦交流电量。

（3）频率相同的正弦量的相量在相量图中的相对位置是固定不变的，所以只有频率相同的正弦量的相量才能画在同一个相量图中，而频率不同的相量不能画在同一个相量图中因为频率不同的正弦量的相量，不同时刻在相量图中的相对位置是变化的。

2.2.3　基尔霍夫定律的相量形式

根据基尔霍夫电流定律可知，在任一时刻流入（流出）电路任一节点的电流的代数和为零。即

∑i=0

式（2-17）中，i可以是常数，也可以是时间的任意函数。对于正弦交流电路，在任意单一频率f作用下，电路中各处的支路电压和支路电流都将是同频率的正弦量。因此，对任一节点来说，在任意时刻，KCL都将成立。即有

对于电流幅值相量，上式仍然成立。即有

式（2-18）和式（2-19）为基尔霍夫电流定律的相量形式。

同理，在任一时刻，沿任意闭合回路，基尔霍夫电压定律可表示为

由上述分析可见，在正弦交流电路中，基尔霍夫定律可直接用电流有效值相量和电压有效值相量写出，或用幅值相量写出；在形式上，正弦交流电路同直流电路的KCL、KVL表达式完全一样。其区别是：电压变换为电压相量，电流变换为电流相量。