交流电基本概念：从电流与电压的角度剖析

众所周知，在直流电路中，电源电压和电流的大小及它们的方向都是固定的，不随时间t的变化而变化。而正弦交流电路中，电源电压、电流和各支路电压、电流的大小和方向都是随时间按照正弦函数的规律变化的；我们把随时间t按正弦函数规律变化的交流电称为正弦交流电。正弦交流电路应用十分广泛。在工农业生产、国防建设及人们的日常生活中用电都是正弦交流电，其主要原因是交流电容易产生和输送，损耗低，电压变换方便、灵活、简单、经济。交流电路中使用的低压电器设备既安全，也容易控制。正弦交流电路同直流电路虽有很大区别，但直流电路中的分析方法原则上都适用于正弦交流电路。分析方法中使用的数学工具由代数法变为复数（相量）法。在我国使用的正弦交流电的频率通常为50Hz（赫兹），称为工业频率，简称工频。

在正弦交流电路中，电压（包括电动势）与电流的大小和方向都是随时间不断变化的，分别用小写字母u（e）和i表示，它们在任一瞬间的电压（电动势）和电流的瞬时值如图2-1所示。

从图2-1可以看出：

（1）正弦交流电压、电流是周期性变化的：波形循环变化1次所需要的时间称为周期，用大写字母T表示，单位为秒（s）。在1秒钟内循环变化的周期数称为频率，用小写字母f表示，单位为赫兹（Hz）。

频率为周期的倒数，即

（2）由于正弦交流电压、电流的大小是随时间而变化的，所以其瞬时值有正有负，且在一个周期内的平均值为零。当波形变化经过横坐标轴时，在这一瞬间电路中没有电流通过，但电压的变化率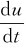≠0。

正弦电压（电动势）、电流统称为正弦量。

2.1.1　正弦量的参考方向

在正弦交流电路中，由于信号源随时间周期性地不断交替变化，因此，电路中各元件上的电压和电流都是时间的函数。为了确定出电路中元件的端电压及通过的电流的实际方向，在分析电路时，要预先设定一个参考方向，如图2-2中实线箭头所示。当电压、电流的参考方向与实际方向一致时，其值为正；反之，若参考方向与实际方向不一致，其值为负，如图2-2中虚线箭头所示。

2.1.2　正弦量的三要素

正弦电压u、电动势e和电流i都是时间t的正弦函数，其数学表达式为

u=U_msin（ω+ψ_u）

e=E_msin（ω+ψ_e）

i=I_msin（ω+ψ_i）

式（2-2）中，u、e、i表示正弦交流电在某一瞬时的电压、电动势和电流的量值，称为瞬时值。U_m（E_m、I_m）、ω和ψ_u（ψ_e、ψ_i）称为正弦量的三要素。

（1）U_m：正弦电压的最大值或幅值，它反映出该正弦量变化的幅度。

（2）ω：正弦电压的角频率，它反映出该正弦量变化的快慢。角频率与频率之间的关系为

由式（2-3）可知，频率越高，角频率越大，变化的速率也就越大。

（3）ψ_u：正弦电压的初相位，简称初相。它是在t=0时的相位角，用度或弧度表示。（ω+ψ_u）称为正弦电压的相位，又称为相位角。

对于一个正弦量来说，知道它的幅度值（最大值）、角频率（频率）和初相位后，就可以用数学表达式或波形图来确定或描述它的全貌。

2.1.3　相位差

在正弦交流电路中，若存在两个以上同频率的正弦波信号，它们只在最大值和初相位上有所差异，如图2-3所示。其表达式为

i₁=I_m1sin（ω+ψ₁）(www.xing528.com)

i₂=I_m2sin（ω+ψ₂）

由图2-3可以看出，当t=0时，ψ₁=0°，ψ₂=90°；当t=t₂时，则ψ₁=90°，ψ₂=180°。由此可见，对于正弦量来说，起始时间不同时，初相位也不同，初相位随着起始时间的变化而变化。

对于两个同频率的正弦量来说，不论初始瞬间选择在何处，初相位如何变化，两者之间的相位差总是不变的。用φ表示相位差，则i₁、i₂间的相位差可表示为

φ=ψ₁-ψ₂

以上讨论的相位差仅限于同频率的正弦量。

2.1.4　有效值

电路的主要功能之一是进行能量转换。交流电的最大值及瞬时值均不能准确地反映其效果。因为正弦交流电是随时间变化的一个量，它的瞬时值在不停地变化着，所以很难用来衡量整个正弦交流量的大小。为此，我们引入有效值的概念，来说明交流量的实际效果和作用。

在电工理论中，有效值是从电流的热效应角度来定义的。在一个周期内，假设通过电阻R上的电流分别为一个直流电流I和一个交流电流i（t），如果产生的热量相等，则这个直流电流I就定义为这个交流电流i（t）的有效值。交流电流与直流电流热效应比较如图2-4所示。

根据定义，假设通过电阻R的交流电流为i，在极短的时间dt内产生的热量为i2Rdt，则该交流电流在一个周期内产生的热量为∫^T₀i²Rdt。如果有一直流电流I通过同一电阻R，经过相同时间T所产生的热量I²RT与之相等的话，则

所以

式中的I即为交流电流i的有效值。同理，对于任意一个周期性交流电压来讲，式（2-5）同样适用。由此可见，当i=I_msin（ω+ψ）时，由式（2-5）可得

同理，对于一个正弦交流电压及电动势，其有效值可表示为

由式（2-6）、（2-7）、（2-8）可知，正弦交流电流、电压和电动势的有效值与其相对应的幅值之间相差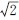倍。根据其幅值就可求出其有效值。

在工程上，一般所说的正弦电压、正弦电流的大小都是指有效值，如交流测量仪表所指的读数、电气设备铭牌上的额定值。但各种器件和电气设备的绝缘水平——耐压值，则是按最大值来考虑的。

【例2-1】已知两正弦电流i₁=2sin314tA,i₂=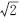sin（314t-45°）A。

（1）在同一坐标上绘出它们的波形图；

（2）求其各自的最大值、有效值、角频率、频率、周期和初相；

（3）说明它们相位差，哪个超前?哪个滞后?

解：（1）i₁，i₂的波形如图2-5所示。

（2）I_m1=2A,I_m2=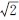A；I₁=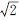A,I₂=1A；

ω₁=ω₂=314rad/s；f₁=f₂=50Hz；

T₁=T₂=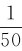=0.02s；ψ1=0，ψ2=-45°。

（3）φ=ψ₁-ψ₂=0-（-45°）=45°；i₁超前于i₂45°，或i₂滞后于i₁45°。