电路基本元件：电感、电容、电源

1.2　电路基本元件

电路元件是电路中最基本的组成单元。电路元件通过端子与外部相连接，元件的特性则通过其电压、电流等物理量来描述，每一种元件反映某种确定的电磁性质。

1.2.1　电阻元件

1.电阻的定义　导体对电流的阻碍作用称为电阻，用字母R表示，其图形符号如图1-4（a）所示。

在国际单位制中，度量电阻大小的单位是欧姆，简称“欧”，用字母“Ω”表示。1欧姆定义为：当导体两端加有1伏特电压，通过导体的电流为1安培时，则导体的电阻数值为1欧姆。即

电阻常用的单位还有kΩ、MΩ等，它们之间的换算关系为

1MΩ=10³kΩ=10⁶Ω

导体电阻的大小是由导体本身的性质所决定的。例如，对于长直金属导线，导体的电阻R与长度L成正比，与它的横截面S成反比，且与导体金属材料的性质有关，这就是欧姆定律，用公式表示为

式中：R——导体的电阻（Ω）；

L——导体的长度（m）；

S——导体的横截面积（m²）；

ρ——导体的电阻率（Ω·m）。

导体电阻率的大小，在数值上等于长度为1m，横截面积为1m²的导体所具有的电阻值。因此，电阻率只与导体材料的性质及温度有关，而和导体的几何尺寸无关。

在相同的温度下，不同的导体具有不同的电阻率，这是由各种导体材料内部结构不同而引起的。即使同一种导体，由于外界温度的变化，在不同的温度下，它们的电阻率也不同。金属导体的电阻率和温度的关系近似为线性关系。当温度升高时，金属内部分子热运动加强，对电流的阻碍作用加大，电阻率就大。它们的关系可表示为：

ρ=ρ₀[1+α（T-T₀）]

式中：T——导体材料的温度（℃）；

　　T₀——参考温度（常取20℃）；

　　ρ₀——T₀时的电阻率；

　　ρ——T时的电阻率；

　　α——电阻率的温度系数（1/℃）。对于不同的导体，温度系数α不同。

2.电阻的伏安特性　电阻两端的电压与电流关系曲线称为电阻元件的伏安特性曲线，图1-4（b）所示是某电阻元件的伏安特性曲线，这种元件称为非线性电阻元件。如果元件的电流与电压成正比，则其伏安特性曲线是一条通过原点的直线，如图1-4（c）所示，该元件称为线性电阻元件。线性电阻元件的符号可用图1-4（c）表示。

3.电阻的串联与并联

（1）电阻的串联：电阻的串联是指将两个或以上的电阻依次连接，使电流只有一条通路的连接方式，如图1-5（a）所示。

电阻串联时流过各电阻的电流相同，电路两端的总电压等于各个电阻两端电压之和，即

U=U₁+U₂+U₃+……+U_n

串联的各电阻可以用一个等效电阻表示，其大小等于各串联电阻之和，即

R=R₁+R₂+R₃+……+R_n

电阻串联时具有分压作用，各电阻上的电压与其阻值成正比。

两个电阻串联时的等效电阻为R=R₁+R₂，分压公式为

（2）电阻的并联：电阻的并联是指将两个或以上的电阻并列的连接在两点之间，使每个电阻两端都承受同一电压的连接方式，如图1-5（b）所示。

电阻并联时各电阻两端的电压相同，电路中的总电流等于各个电阻上的电流之和，即

I=I₁+I₂+I₃+……+I_n

并联的各电阻可以用一个等效电阻表示，其大小是等效电阻的倒数等于各串联电阻倒数之和，即

电阻并联时具有分流作用，各电阻上的电流与其阻值成反比。

两个电阻并联时的等效电阻为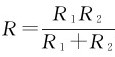，分流公式为(www.xing528.com)

1.2.2　电感元件

1.线性电感元件　常见的电感元件就是用导线绕制的线圈，当线圈通以电流产生磁场变化时，在线圈中就产生感应电压。当穿过线圈总磁通ϕ和通过它的电流i成正比时，此电感为线性电感元件，比例系数称为自感系数，用L表示，符号如图1-6所示。

在国际单位制中，电感的基本单位是亨利，简利亨，符号用H表示。电感的其他单位还有毫亨（mH）、微亨（μH）。

1H=10³mH=10⁶μH

2.电感元件的电压、电流关系　当通过电感中的电流i发生变化时，两端就存在感应电压u_L。在电流、电压取关联参考方向的情况下，根据电磁感应定律有

电感上的电压与电流取非关联方向时，则有

从式（1-10）可以看出，任何时刻，线性电感元件的电压与该时刻电流的变化率成正比。当电流不随时间变化时（直流电流），则电感电压为零，这时电感元件相当于短接。

电感元件是储能元件，储存磁场能量，大小为

1.2.3　电容元件

1.线性电容元件　电容元件从构成原理上来说，由间隔以不同的介质（如云母、绝缘纸、电介质等）的两块金属板极组成。它是一种能储存电荷的元件，其储存电荷的能力叫电容，用C表示，如图1-7所示。

若电容存储电量与加在两极上的电压成正比，则称为线性电容。即

在国际单位制中，电容的基本单位是法（拉），符号为F，其他常用单位还有微法（μF）和皮法（pF）。

1F=10₆μF=10₁₂pF

2.电容元件的电压、电流关系　在电容元件上，若取关联方向，则

从式（1-11）可以看出，流过电容的电流与电容两端的电压变化率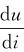成正比。直流时，由于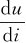=0，则有i_C=0，即对于直流相当于开路。

电容也是储能元件，其储存电场能量大小为

1.2.4　电源元件

1.电压源　电压源也叫恒压源，如图1-8所示。它具有以下特点：电压源两端的电压U_S（t）为确定的时间函数，与流过的电流无关；当U_S为直流电源时，两端的电压不变，U_S（t）=U。直流电压源伏安特性如图1-9所示。

电压源只是一种理想的情况，实际电源不可能如此。实际的电压源可以用电压源和一电阻（内阻R₀）的串联模型表示，如图1-10所示。

2.电流源　提供恒定电流的电源称为电流源，又叫恒流源，如图1-11所示。电流i_S（t）是确定的时间函数，与电流源两端的电压无关。在直流电流源的情况下，输出的电流是恒值，I_S（t）=I。

直流电流源的伏安特性如图1-12所示。

电流源也是一种理想的情况，实际的电流源可以用电流源和电阻（内阻R₀）的并联模型表示，如图1-13所示。

3.电压源与电流源的等效变换　图1-10所示的实际电压源模型和图1-13所示的实际电流源模型都可作为同一实际电源的电路模型，可以有相同的外特性。因此，相互之间可以进行等效变换，如图1-14所示。电路的等效变换有时能使复杂的电路变得简单，便于分析计算。其等效规律为：电源的内阻不变，且U_S=I_SR₀。

在进行电压源模型和电流源模型的等效变换时还需要注意：

（1）等效变换是对外电路等效，对电源内部不等效。例如当外电路开路时，电压源模型中无电流，内电阻不消耗功率；而电流源模型中仍有内部电流，内电阻要消耗一定的功率。

（2）等效变换时两种电路模型的极性必须一致，即电流源模型流出电流的一端与电压源模型的正极性端相对应。

（3）理想电压源和理想电流源之间不能进行等效变换，因为理想电压源的内阻R₀=0，而理想电流源的内阻R₀=∞，两者不满足等效变换的条件。再者，理想电压源的电压恒定不变，电流随外电路而变；而理想电流源的电流恒定，电压随外电路而变，故二者不能等效。

【例1-1】如图1-15（a）所示电路中，已知U_S1=130V,U_S2=117V,R₁=1Ω，R₂=0.6Ω，R=24Ω。试求负载R上的电流。

解：利用电压源模型与电流源模型的等效变换关系，将电压源模型变换成电流源模型，如图1-15（b）所示。图中：

I_S1=U_S1/R₁=130/1=130A

I_S2=U_S2/R₂=117/0.6=195A

然后将两个并联的电流源模型合成一个等效的电流源模型，如图1-15（c）所示。图中有

IS=IS1+IS2=130+195=325A

所以负载电流