J.P.Giroud的设计方法优化

早先，Giroud and Noiray（1981）建议按下列准则选择无加筋的无铺砌道路的厚度。

式中：N为标准轮轴通过次数；h为道路厚度，m；CBR为加州承载比（CBR）系数。

近年，Giroud又提出了一种新的设计方法，介绍如下：

图11.27所示为无铺砌道路的示意图和它的当量接触面积。

设加筋材料铺设在基层与地基之间，地基土在影响深度范围内（1.5m左右）是均匀的，最小基层厚度取0.1m，以使基层可以施工，并减少通车时对地基土的扰动，同时对格栅提供足够的锚固条件。

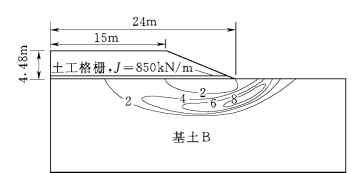
图11.27　在4.5m高加筋堤下地基（剖面B）中最大剪应变等值线图

（在竣工期至固结度98%时加筋应变增加2.4%）

Giroud发展的方法是基于下列的原理，对无铺砌道路，当车辙深度达到允许车辙深度时（75mm），道路的可用性就丧失了。该深度取决于地基土的变形，而这又与地基土界面上的应力有关，因此方法的发展是基于两个方面：①确定基层/地基土界面上的应力；②确定车辙的深度（将它作为基层/地基土界面上应力的函数）和地基上的承载力。在这中间，应力分布角（stress distribution angle）起了一个重要的作用，因为它控制了轮轴通过次数和土工格栅对基层所需厚度的影响。

11.3.2.1　地基土的应力

假定道路上所施加的一个轮子或一对轮子的荷重均匀地分布在一个半径为r的圆形面积上，同时假定应力是根据应力分布面角α而分布的，于是在分界面上的法向应力pi可由式（11.8）确定：

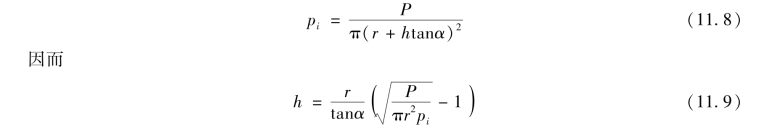
式中：pi为作用于分界面上均布的法向应力，kPa；P为轮压，kN；r为轮胎接触面的当量半径，m；α为应力分布角。

由于应力分布可以用单一参数α来表达，因此可以方便地用来确定所需的基层厚度。

11.3.2.2　基层所需的厚度

基层与地基分界面上的均布法向应力（压力）pi应满足下列的要求，以防止地基土的破坏：

式中：m为承载力发挥系数，承载力的发挥系数（0≤m≤1）是由于考虑到地基土的承载力只有一部分可以发挥；Nc为承载力系数；Cu为地基土不排水黏聚力。

将上两方程相结合可得出：

式中有3个未知数：承载力系数Nc，承载力发挥系数m，应力分布角α。它们将在下面讨论。

11.3.2.3　承载力系数Nc

对于土工织物加筋的无铺砌道路，Giroud等（1981）已建议采用：Nc=5.14（即π+2），因为这是饱和不排水地基土的最终承载力（ultimate bearing capacitg）。而且这是相应于平面应变二维的情况。

对土工格栅加筋的情况，最终承载力系数的理论值对于平面应变二维情况为NC=5.71（3π/2+1），这是由于两种机理而导致的：①基层材料的侧向位移受到限制；②粗粒穿入格栅的孔洞，在分界面上产生了最大的摩阻力，故地基土的侧向移动受到限制，由此，在地基中产生了最大向内剪应力。于是地基土的承载力系数由5.14增大到5.71。

对轴对称的情况，该最大界面向内剪应力的理论值为5.69～6.04。

根据上述论证，承载力系数的选择如下：无铺砌无加筋道路NC=3.14；土工织物加筋的无铺砌路NC=5.14；土工格栅加筋的无铺砌路NC=5.71。

11.3.2.4　承载力发挥系数m

当基层厚度为零时，车辙的允许深度为75mm的承载力发挥系数取为1.0，然后随基层厚度的增加而减小。因此，当可用性准则（the serviceability criterion）为一允许车辙深度75mm时，承载力发挥系数由式（11.12）确定。

式中：ξ，ω和n为未知参数，将在下面介绍的试验成果中确定。

（Giroud等，2004）若可用性准则不是75mm的允许车辙深度，则承载力发挥系数与实际的车辙深度成正比，即

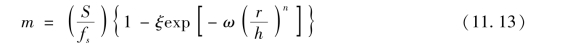
式中：S为允许的车辙深度；fs为一常数，其值等于75mm。

式（11.13）仅可用于车辙深度在50～100之间的范围内。

结合式（11.11）和式（11.13）可得出下列的方程，它适用于加筋和无加筋的情况。

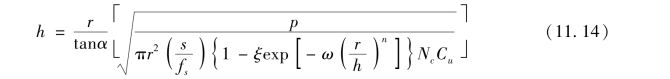
式中：h为所需的基层厚度，m；r为等效轮胎接触面的半径，m；P为轮胎荷载，kN。

11.3.2.5　极限情况下的承载力

若基层厚度为零，则由式（11.10）可得承载力为

当h=0时，由式（11.12）可得：

结合式（11.15）和式（11.16）有：

式中：fs为车辙深度，fs=75mm。

由于Cu=fcCBRsg，CBRsg为地基土的加卅承载比（Giroud和Noiray，1981），则其中，Nc=3.14，对无加筋情况；Nc=5.14，对土工织物加筋情况；Nc=5.71，对土工格栅加筋情况。

11.3.2.6　应力分布角的影响因素研究

前已指出，本法是用应力分布角α来估计由外荷引起的应力的分布，为此，须研究各种因素诸如①基层材料和地基土的特性；②交通荷载的状况；③土工格栅的性质对应力分布角的影响。但应力分布角没有物理的真实性，故不可能直接进行量测，也不能直接进行理论计算，而只能采用间接估算。在该法中，首先是量测或计算在特定位置上（例如在基层与地基的交界面上）的垂直应力，然后根据在荷载中心线上的当量最大垂直应力计算。应当注意，最大应力是很重要的，对于细粒土地基上不排水加荷，局部破坏往往是从最大应力点开始的。

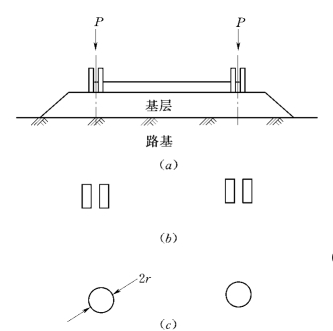
图11.28　轴距和接触面积

（a）双轮车轴的几何形状；（b）轮胎接触面积；（c）分析所用的当量接触面积

（1）基层和地基土的性质对应力分布角的作用。对于具有基层和地基的双层结构，基层往往比地基上具有较高的弹性模量。两层之间分界面上的垂直应力（在循环荷载轴上）随上下两层模量比的增加而降低。但要计算该垂直应力比较复杂，因此，可以用应力分布角法计算。而该角则与基层和地基土两者的模量有关。这个关系取决于r/h，其中r为轮胎当量接触面积，h为基层的厚度。该值最可能的范围为0.2～2.0。当r/h在该范围内时，垂直应力与模量比已有定量的关系，然后平均应力分布角α可在荷载中心线上的当量最大垂直应力的基础上求得。如图11.28所示，应力分布角的正切的比值是基层模量与地基土模量的比值。其公式如下：

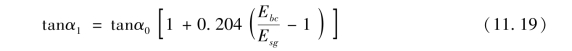
式中：α1为当Ebc≠Esg时的应力扩散角；α0为参考介质（材料）在Ebc=Esg时的应力分布角；Ebc和Esg分别为基层和地基土的模量。方程（11.19）适用于静荷载。

结合式（11.7）和式（11.19）可得：

式中：RE为极限模量比，定义为：

同样，模量比系数fE在分析中采用：

由式（11.20），可以根据任何的静力扩散角α1，推导出基准（reference）应力分布角α0，该值与基层或地基土的性状无关。

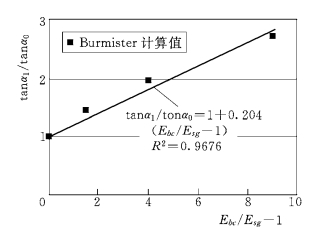
图11.29　应力分布角与模量比的关系

（2）交通荷载对应力扩散角的作用。应力扩散角会随道路加荷次数的增加而降低，是logN的线性函数（如图11.29），并可表为

式中：α为N次受荷的应力扩散角；α1是对应于加荷次数为1时的应力扩散角；K为常数，取决于基层厚度和加筋材料。

从该式可知，α与N关系取决于两个参数：即（α1为道路加荷一次时的应力扩散角）以及常数K，对该参数作如下的讨论：

当N=1时，由图11.29上的曲线可知，，即

α1值为一常数，它可由式（11.20）转为基准的（reference）应力扩散角α0。根据动力触探试验，地基土和基层的CBR值各为5.0和20.0。因此

而根据试验，。

结合式（11.24）可得

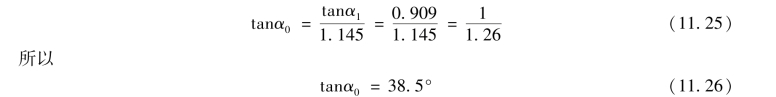(www.xing528.com)

由此可知，对一均匀土，应力扩散角有唯一的值，但该值与用来估计α0值的方法有关。这里所用的方法是基于荷重中心线上的当量最大垂直应力。

第二个参数是表征α1和加荷次数关系的常数K，它与边坡λ有下列关系：

结合式（11.20）和式（11.23）给出

结合式（11.14）和式（11.31）给出

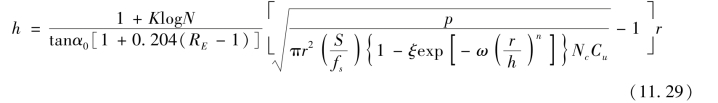
式中：p为轮胎荷重，kN；其余符号意义如前。

式（11.29）是由基层厚度和logN之间的线性关系的一般形式组成。由此进一步验证了式（11.23）的线性关系。

根据对基层厚度为0.15m和0.25m的土工格栅（B11和B12）以及无加筋情况的试验得出，轴压通过的次数和应力扩散角的关系可由两个参数来表征：即N=1时的1/tanα（即1/tanα1）和1/tanα～logN曲线的坡度λ，因为1/tanα～logN的关系近似为一直线。而且已知1/tanα1=1.1为常数，故λ仅受格栅筋材和基层厚度的影响，如图11.29所示。该图的关系可用式（11.30）很好地近似表达：

式中：J为格栅的孔洞的稳定模量（aperture stability modulus），MN/°；B、C、D和x为未知的常数，其中C很小可忽略，而x根据试验成果可取1.5。

于是用式（11.30）进行试算，可得

11.3.2.7　设计的公式

由式（11.30）可转化为下式：

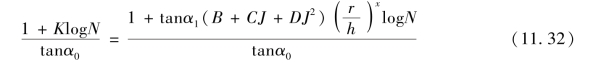
将式（11.27）、式（11.28）和上述的B、C、D，x值代入上式，可得

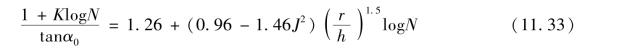
结合式（11.29）和式（11.33）可给出基层厚度的计算公式：

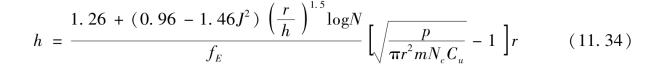
其中，fE的计算如式（11.22）所述，而m的计算如式（11.13）所述。

当无加筋时

J=0由试验结果得出，若要用于无铺砌道路，则尚需采用现场试验结果进行校准。

式（11.34）中的常数由实验室循环荷试验中求得。但它不能代表真实的现场情况，故还需用现场的资料。式（11.34）中的未知常数（ξ、ω和n）定义了承载力发挥系数，它也应由校准过程中确定。

为便于考虑现场情况的a、b、d等常数的校准，可将式（11.34）式改写成：

式中：h*为归一化的基层厚度。

h*定义为

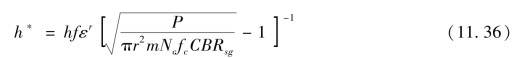
式（11.36）中，常数a、b、d对照式（11.34）可知，a=1.26，b=0.96，d=1.46，而在设计中真正采用的值还考虑现场与实验室差别的因素。如图11.30所示。

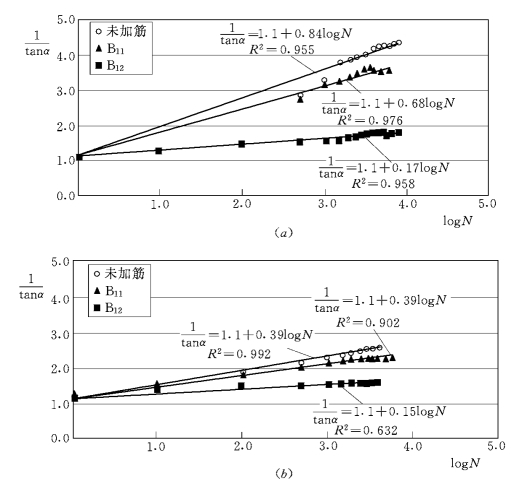
图11.30　应力分布角与通过次数的关系

（a）基层厚度0.15m；（b）基层厚度0.25m

将现场数据点绘于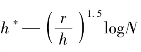坐标系上，由回归分析可得（图11.31）。

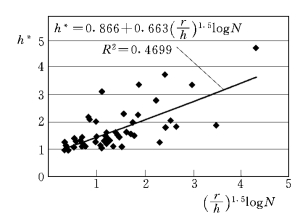
图11.31　参数a，b的确定

由式（11.13）可知，m值与ξ的取值有关，也取决于ω和n值。由于r/h较小，ξ值须接近于1.0，取ξ=0.9。而ω和n取为1.0和2.0，故

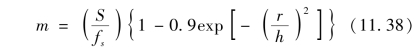
d的校准值的确定如下：

先计算由现场试验求得的afield和实验室试验求得的alab；以及相应地bfield和blab，然后计算：

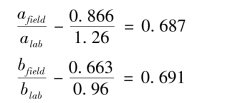
上述两比值的平均为0.689，用该值来校准a、b、d，以考虑现场的条件，则为按此反算的dfiled back（或记为df，b）

类似地以0.689来校准a和b，可得

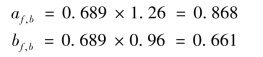
可以认为af，b，bf，b以及df，b将是a、b、d的最优校准值。

11.3.2.8　设计过程

先按下式计算当量接触面积的半径r，并选用允许车辙深度为75mm。则

地基土的不排水黏聚力Cu可由式（11.40）确定：

式中：p为轮胎接触压力；CBRsg为地基的加卅承载比；fc为系数，其值为30kPa。地基上的CBRsg和不排水黏聚力Cu应为已知（Cu也可由CBRsg求得）。

步骤1：校核天然地基在不加筋情况下，能否支持车辆荷载，即P是否大于地基土的承载力或可依式（11.18）计算，此时Nc=3.14，该承载力与车辆的轴压次数无关。若承载力足够，则无需加筋，否则应设基层并加筋。

步骤2：确定所需的基层厚度（加筋和无加筋的），该式需进行迭代。

先定一个基层的起始厚度，它可根据设计图（图11.32）设定。将设定的厚度代入式（11.29）等，可得所需的基层厚度，重复计算几次，直到计算厚度与所设定的厚度相等或相近时，则结束计算。如果所得的计算厚度小于0.1m，则采用0.1m。

【例】　条件：选用B12土工格栅，它的孔洞稳定模量为0.65mN/°，对于一个无铺砌道路，在40kN的轮荷（胎压力为550kN）下进行5000次循环。地基土的CBR为1.0，现场压实后土的CBR为1.5，允许车辙深度为75mm。

解

Cu可由CBRsg求得。

第二步，计算无加筋下地基土的允许承载力Ph=0，unr

可见，Ph=0，unr小于轮荷40kN，故应设置基层。

下一步，在求基层厚度之前应先求出极限模量比RE和模量比因素fE。RE应取和5.0中的小值，因为，故RE=5.0。

按式（11.22），fE=1+0.204（RE-1）=1+0.204（5.0-1）=1.816，再下一步进行所需基层厚度的迭代计算，先计算无加筋无铺砌道路的情况，设其厚度为0.4m，则承载力发挥系数m的计算为

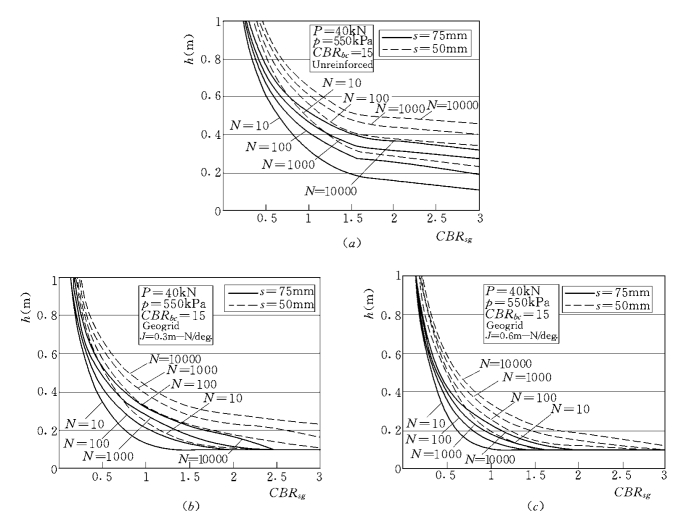
图11.32　未加筋和格栅加筋路堤设计图

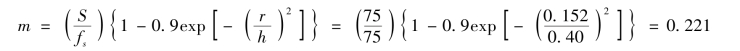
应用方程（11.41），且对无加筋情况，NC=3.14，J=0时，则首次迭代的厚度为

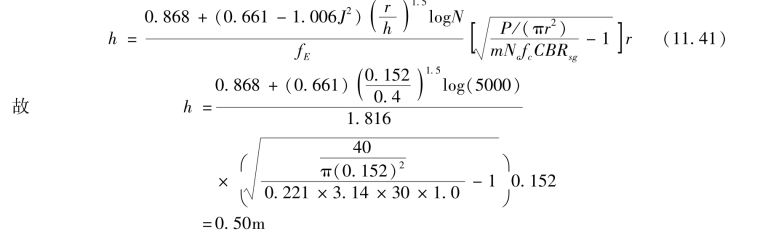
注意，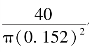

代表轮胎接触压力，可用550kPa代之。

计算的厚度大于起始假定的值0.4m，为此再用0.5m作为假定厚度进行再计算，得到的再计算厚度为0.5m，因此计算成功。但此为无加筋情况。对于土工格栅的加筋，r和fE与无加筋相同，但假定首次迭代的基层厚度为0.25m，可得：m=0.378，再就用式（11.41）以及Nc=5.71，J=0.65mN/°，则基层厚度为h=0.21m。该值小于起始设定值0.25m，故用0.25m作为设定值再作计算，最后得加筋基层厚度为0.18m。