软基上加筋路堤设计要点

软土地基上堤坝设计的第一步是估计是否需要加筋或加固，以使设计的堤坝在地基软土层不排水的条件下，能够稳定而不塌陷。假如设计的安全系数不能达到要求的数值，则就需要措施加筋或加固，这可以通过验算地基的承载力来实现。

11.2.2.1　加筋堤的常规设计方法和实例

软基上加筋堤的破坏有如下几种形式：

（1）浅层水平滑动，软土厚度较小的加筋堤。

（2）深层圆弧滑动，软土层较厚的加筋堤。

（3）地基整体承载破坏。

（4）地基在加筋堤破坏之前发生较大的变形，堤坝无法正常工作。

除此以外，筋材的断裂也会导致路堤破坏。图11.2为筋材断裂和地基土挤出破坏的情况。

图11.2　加筋土堤筋材断裂和地基土挤出破坏

（a）筋材断裂破坏；（b）地基侧向挤出

上述几种破坏形式的分析方法简述如下。

（1）厚层软基上的加筋堤。土工合成材料的作用姑且视作增加一个抗拉力，若筋材不被拉断，则该拉力就是筋材与土的摩擦阻力相应的那部分强度。计算可采用一般圆弧滑动的简化Bishop条分法进行（对此不再详述）。

下一步是筋材的选择，根据加筋后安全系数的要求，求出筋材所需的容许抗拉强度，加筋的范围（长度和宽度），以及筋材铺设的层数，在设计中应验算筋材的抗拔力。

（2）浅层软基上的加筋堤。

1）沿下卧硬层顶面滑动[图11.3（a）]，抗滑安全系数按式（11.2）计算

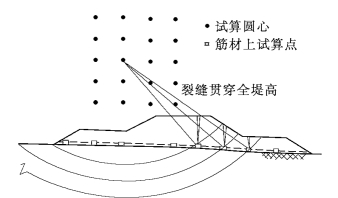
图11.3　加筋堤圆弧滑动分析

2）沿筋材顶面滑动[如图11.4（b）]，抗滑安全系数按式（11.3）计算：

式中：PA为主动土压力；FB为滑楔底面上的抗滑力，随土坡填料和筋材不同而不同，但不得大于筋材的容许抗拉力。

图11.4　浅薄层软基上加筋堤的稳定性核算

（a）沿硬层顶面滑动；（b）沿筋材顶面滑动

（3）加筋堤设计的承载力分析（Rowe 1992）。假定加筋堤可按整体基础求解地基承载力，加筋堤基的极限承载力qo为

式中：Nc为承载力因素，该式是针对宽度为b的刚性基础的。对于梯形堤剖面，应近似地转变为等效基础宽度b0，b0=B+2n（H-h），如图11.5所示。

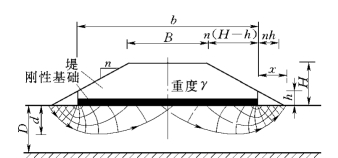
图11.5　基础等效宽度

11.2.2.2　有限元分析法

采用有限元法分析软基上加筋堤的稳定性问题有重要的应用价值。与常规的极限平衡法相比，它最大的特点是，除了在计算中能考虑实际施工过程和复杂的边界条件以及土性参数之外，更能给出从施工到运用的全过程中应力和变形的发展，并对建筑物的稳定性作出判断。从而对设计者预示出所设计的结构物在各个阶段的工作性状，及早发现设计的不足及采取适当改进措施。同时，有限元法在进行方案比较和敏感性分析中也特别有其用武之地。

在有限元分析中，本构关系的选择，土性和其他材料参数的确定，边界条件的考虑，施工顺序的安排等基本问题的正确与合理的选择，对计算成果的真实性特别重要。这里将对这些问题稍作叙述。

（1）本构关系。根据已有应用有限元分析的经验，不同的物质（材料）应有针对性的本构关系，在加筋堤中，这些物质（或材料）有地基土、堤坝填土、加筋材料和土—筋材的界面等。对于地基和堤坝填土一般采用非线性弹性模型和比较成熟的弹塑性模型为宜，对于加筋材料大都采用线弹性模型或非线性弹性模型（如邓肯—张模型）。对土—筋界面的情况比较复杂，因为在以后的机理分析中将会看到，这个“界面”不是一个无厚度的接触面，而是有一定厚度的剪切带（包含该接触面）（张嘎，2004）以及剪切带外面的影响带，有关问题将在后面讨论（包承纲，2006）。关于加筋地基的固结分析，可以采用耦合了比奥固结理论的非线性弹塑性模型。黏塑性模型可用于高灵敏性软土地基上随时间变化的加筋堤坝的性状研究（Rowe和Hinchberger，1998）。当用蠕变不显著的筋材加固堤坝时（如聚酯PET土工格栅等），可利用一维杆单元结合线性或非线性弹性本构关系。对蠕变敏感的筋材（如polyolefin土工格栅），其蠕变和松弛可以用非线性黏弹性或黏塑性模型来描述（Li和Rowe，2001）。就工程应用来说，当作用剪应力不大于界面摩阻力时，认为界面无相对位移。并设界面摩擦角δ等于土体的内摩擦角φ。总之，所选的本构模型应简单、实用、有一定的应用经验为宜。

（2）土性参数。土性参数对计算的精度和真实性是十分重要的，不同的本构模型有不同的本构参数，这些参数应尽可能由试验实测确定，而以经验值作为参照量，并尽可能在实际中不断修正和更新（updating），或用反分析法进行校正。

（3）边界条件和加荷过程。这些边界条件应在尽可能真实的前提下进行简化，所设定的边界条件应基本保持它的原来物理性状。加荷过程划分的粗细也对成果有相当影响，应在计算机允许的条件下适当细一些。施工的间歇期一定要模拟。

11.2.2.3　若干实例

（1）【例1】两座修建在极度软弱黏土上的堤坝，一座加筋，一座未加筋，用有限元法进行了对比计算，堤基为厚度约3.3m的软黏土，其不排水强度为8kPa，下卧为砂。

对未加筋堤，当填筑高度达1.8m时其位移场和塑性区如图11.6所示，表明该区通过坡趾，且切于底部硬层顶面，区内所有点的剪应力都达到了其抗剪强度。该堤实际观测到的破坏发生在堤高1.75m时，表明与计算预测相当接近。

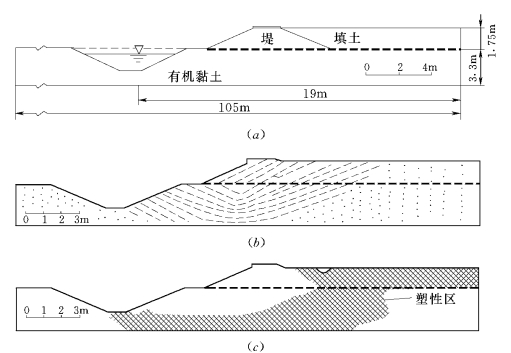
图11.6　未加筋堤的有限单位法计算结果

（a）1.75m时破坏；（b）1.8m时的速度场；（c）1.8m时的塑性区

对于加筋堤，当填筑至2.75m且经过一天后才发生破坏，由此看出加筋的作用。从图11.6和图11.7可以看出，当加筋堤加载到1.8m时，其塑性区范围不很大，且不贯通（图11.6），仅当加载到2.05m时，中塑性区相互连通（图11.7），但真正达到破坏则在填筑高度达2.66m时，这与实测的破坏高度2.75m也相当吻合。

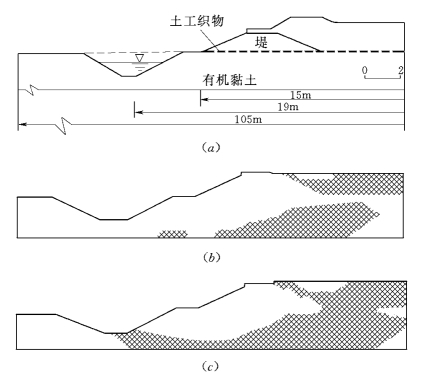
图11.7　加筋堤有限单元计算结果

（a）2.75m时破坏；（b）1.8m时的塑性区；（c）2.05m时的塑性区

（2）【例2】Muar黏土上的加筋堤。在马来西亚Muar黏土上建造了用两种土工格栅加筋的两座堤坝，其中一个具有反压堤，另一个无反压堤。采用有限元法对其进行了分析。并将FEM的结果与实际观测资料（超孔压、沉降、侧向变形等）作了对比，具有较好的一致性。

对于地基，FEM的计算模型采用修正剑桥模型，M、λ和K由试验室确定，对于渗透系数，考虑到实验室的成果往往偏低（Tavenas and leroueil，1980），故垂直渗透系数假定等于两倍实验室结果，而水平渗透系数假定等于垂直的两倍。对于填土采用双曲线模型，其强度参数来自不固结不排水三轴试验，其他参数参照Duncan的资料（Duncan等，1980），土工格栅铺在砂垫层上，设砂的φ=38°，c=0，γ=20.5kN/m3。土与筋材的接触面采用直剪模型和拉拔模型。

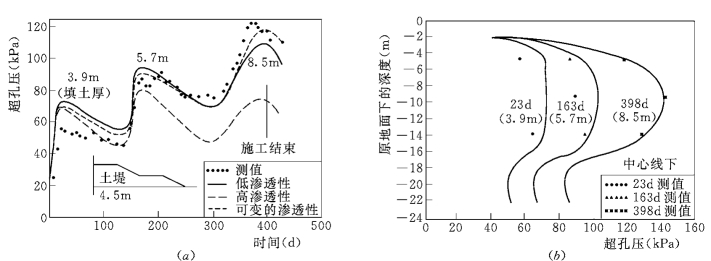
研究表明，计算的与观测的值一般都有良好的一致性，只是侧向位移稍微差些。图11.8和图11.9表示了沿堤A中心线超孔压的过程和分布的剖面，图11.9表示了堤A的表层沉降剖面。可以看出，在施工早期（3.9m填土厚度），在堤趾处有限元法求得的沉降比堤中心线上沉降要大，实测结果反映了相同的规律，其原因可能是该处的剪应力较高。这种现象表明，在堤坝施工的最初阶段，软基上的堤坝产生了显著的固结。

(www.xing528.com)

图11.8　试验堤A的超孔压曲线

（a）时程图；（b）剖面分布图

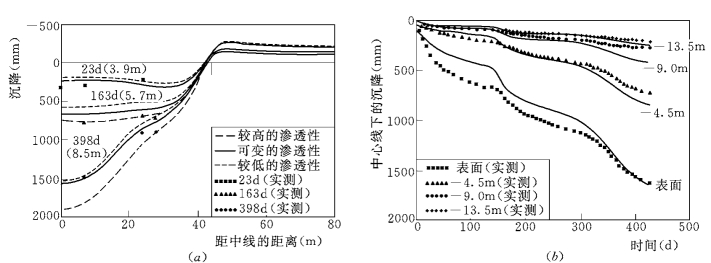
图11.9　堤A的沉降实测资料

（a）堤A的表面沉降剖面；（b）典型的沉降过程线

图11.10表示了计算的和实测的侧向位移值与深度的关系，图11.10中表明，在早期阶段，计算值与实测值有一定差别。

堤A和堤B首期填筑到3.9m，两者的最大侧向位移基本相同，为200mm左右。以后，当填土3.9～6.0m时，对于具有较强筋材并设有反压堤的A堤，最大侧向位移从200mm增加到325mm，而对于较弱筋材和无反压堤的B堤，其最大侧向位移由200mm到480mm。如图11.11所示，A堤的两层土工格栅对最大侧向位移没有很大的影响，而A堤的反压堤起了较大的作用，这点在设计加筋堤时是很值得注意的（Chai J C.，1993）。

11.2.2.4　加筋堤的离心模型试验及有限元分析验证

（1）缘由。近几年来，利用离心模型试验研究土工合成材料加固的软土地基上堤坝的实例已越来越多。这里介绍软基和吹填土上堤坝排水条件及织物布置形式对加筋堤稳定性影响的离心模型试验成果。加筋堤在实际施工时，不同施工方法、施工条件都会对加筋效果产生很大影响。

吹填土是利用水力机械冲搅泥沙，由泥浆泵通过管道输送到淤区，逐渐脱水固结形成的一种特殊性质土，其初始强度极低。如何在吹填土上筑堤是一个难题。用离心模型试验模拟土工织物砂垫层加固吹填土，结果证明这是一种较为有效的加固措施（丁金华，包承纲，1999）。

（2）工程及试验概况。试验是在长江科学院300gt离心机针对宁波东钱湖湖心岛堆筑工程进行的。该工程主要是挖除湖中淤泥，经疏浚吹填后形成湖心岛。工程初步设计方案见图11.12。

先利用堆石建成第一级拦淤堤，然后在堤内吹填挖出的淤泥，待吹填土达到一定强度后，在其上用袋装土建成第二级、第三级、甚至第四级拦淤堤，并继续吹填至最终高程7.0m。

地质钻探资料表明，东钱湖湖底淤泥厚度薄处1m，最厚达15m，由湖南部向北逐渐变深。土层为海相沉积，夹有贝壳碎片，呈流塑状态。从南湖2.0～3.0m深处取回的原状淤泥土样的物理力学性质指标见表11.1。

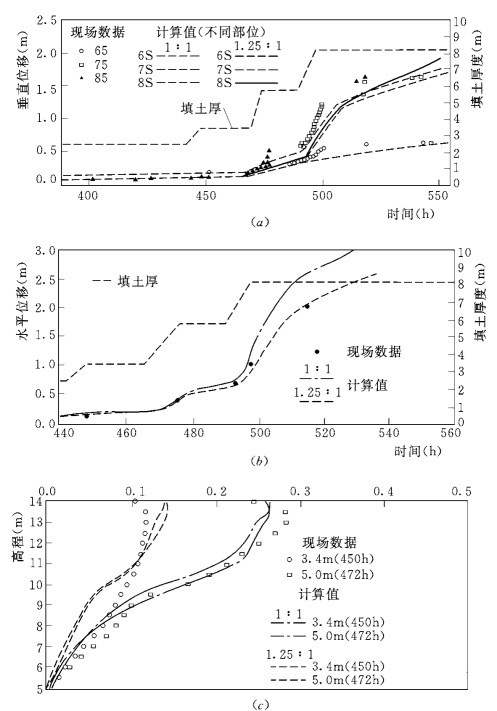
图11.10　计算的和实测的垂直变形和水平变形的比较

（a）垂直位移与时间关系；（b）堤趾的水平位移（m）；（c）相对位移剖面（测斜仪231）

用原状淤泥配制成w=250%～300%的泥浆，置于室内静水下沉积，经10～35d后，含水量可降至90%～100%，但强度极低，用环刀无法取样，十字板强度仅0.5～1.0kPa。因此为保证工程顺利进行，必须对软基和吹填土进行加固。

设计拟采用土工织物砂垫层及垂直排水带联合处理措施。土工织物直接铺设在淤泥和吹填土表面，其上有0.5m的砂垫层。第一级堆石拦淤堤高4.4m，垂直排水带间距为1.5m，贯穿软土层及吹填土，试验中控制吹填土的初始含水量接近90%。考虑不同排水条件、不同土工织物布置方式等因素的影响，进行了三组对比试验，各模型断面见图11.13。

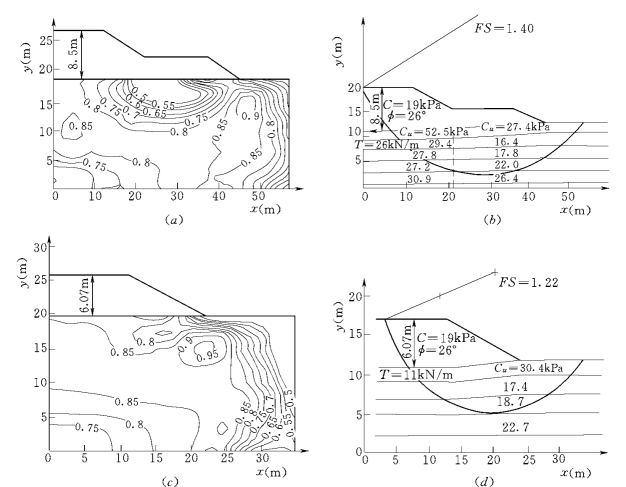
图11.11　反压台与加筋对土堤稳定的作用

（a）剪应力水平等值线（有反压台）；（b）圆弧分析（有反压台）；（c）剪应力水平等值线（无反压台）；（d）圆弧分析（无反压台）

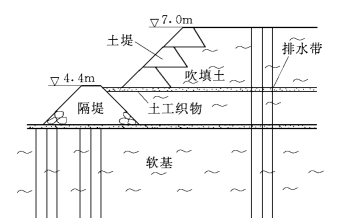
图11.12　东钱湖工程简图

表11.1　东钱湖淤泥物理力学性质

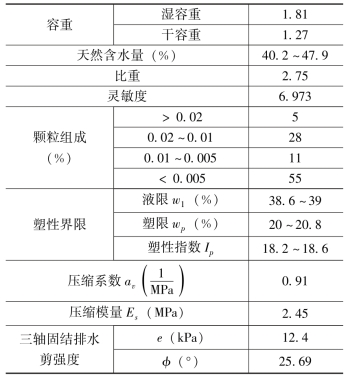
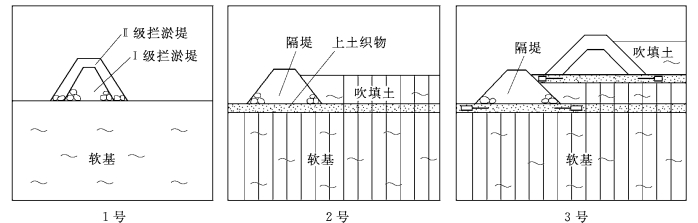
图11.13　离心模型试验模型简图

1）1号天然地基，第一级拦淤堤分两级施工。

2）2号地基经加固处理后，对第一级堆石拦淤堤和吹填土进行同步施工，土工织物两端未锚固，排水条件不良。

3）3号地基经加固处理，对各级拦淤堤和吹填土进行分级施工，土工织物两端锚固，完全排水。

模型比尺均为1∶70，软基模拟15m，试样用从现场取来的原状土样制备，考虑到东钱湖淤泥的灵敏度较高，为消除扰动的影响，先把制好的地基模型放入离心机中，开动机器，让模型在n=70g下固结一定时间，然后再取出，用石渣料模拟堆石，施加上部隔堤荷载。试验中用位移传感器监测各级拦淤堤堤顶及地基表面的沉降变化。以离心机逐步加速来近似模拟填土速率，以恒定转速下的试验来模拟施工间歇期或运行期的工况。

试验中所用土工织物采用一种极薄的热黏性无纺织物，由宽条拉伸试验得出其破坏应变约10%，抗拉强度为249.8N/m，浸水后无强度损失。采用强度相似模拟原理，可知其相当于原型土工织物抗拉强度17.5kN/m。

（3）试验过程及结果分析。对模型1号，用12min时间（相当于原型41d）将本试验加速到70g，此时模型堤顶瞬时下沉5.5mm，相当于堤顶瞬时沉降0.385m，稳定运转60min（原型204d）后，堤顶沉降达0.665m。从沉降—时间曲线上来看，堤顶沉降并未稳定，仍在继续发展。停机，将拦淤堤加高至7.0m，加载20min（原型68d），并稳定运转160min（原型544d）后，堤顶沉降累计达1.70m。地基面沉降0.537m。

此模型表明，不处理天然地基，而采取分级施工方法，可以保证第一级拦淤堤的稳定，但软基和隔堤的变形较大。

对模型2号，同步施加4.4m堆石隔堤和4.2m厚的吹填土，w=94.2%，用15min（原型51d）加载至70g，然后稳定运转到180min（原型612d）停机。由位移传感器所显示的变形曲线上看出（图11.14），加载过程中隔堤堤顶及地基表面均发生隆起现象，分别达0.735m和0.175m；但在稳定运转时，堤顶和地基表面不再继续隆起，而是向下沉降。取出模型箱后，观察到吹填土从堤底挤向另一侧，地基出现较明显的侧向位移。说明若同步施加隔堤与吹填土荷载，且填土速率又较快时，地基会因本身抗剪强度不足以抵抗上部不均匀荷载而发生塑流破坏，吹填土从堤底挤出。

图11.14　模型2号变形—时间曲线（图中所标数值系对模型而言）

在这次试验中，土工织物两端自由，测得其变形仅1.3%，说明土工织物并未起到应有的加筋作用；而模型箱的外部排水条件较差，试验结束后吹填土上部积水未排出。

模型3号改进了排水条件，土工织物两端包裹在砂垫层内。按照第一级堆石隔堤4.4m→第二级吹填土4.2m→在吹填土上建第三级土堤2.0m→加高土堤至5.0m→继续吹填至高程7.0m的加载顺序进行。本次试验获得了较好的结果，吹填土没有发生挤出，地基虽有一定的侧向变形，但仍保持整体的稳定性，未发生明显的滑弧破坏。其中第二级吹填土经140min（原型474d）固结后，测得十字板强度为6.2kPa。根据γH=5.14c得到相应极限填土高度仅为1.7m，经过土工织物砂垫层处理后，一次填土2.0m。然后再使其完全排水固结80min（原型272d）后，吹填土仅发生均匀沉降0.35m，十字板强度已提高到14.7kPa。当继续加高土堤到5.0m，比极限填土高度4.1m高出0.9m时，软基及吹填土仍未破坏，此时吹填土含水量已降至48%。由此说明当土工织物两端锚固，堆石隔堤和吹填土分级施工且控制加荷速率时，工程是可以稳定的。

（4）试验成果验证。采用有限元分析法对离心模型试验的成果进行验证。

加筋土的有限元分析模式有两类：一类是将土体、筋材分别考虑，一般对土体采用现有的本构模型，而将筋材视为一维杆单元；另一类是把加筋土作为复合材料，通过试验得到复合强度参数。

本文尝试一种新的分析模式，即考虑土工织物的厚度因素，用二维实体单元来模拟，近似符合理想弹塑性体性质。由于土工织物沿厚度方向的变形远远小于其长度方向变形，因而可认为厚度不发生变化，泊松比取一很小值。

土体采用非线性的双曲线模型。软基淤泥和砂垫层采用E—v模式，对堆石隔堤采用E—B模式，由三轴固结排水试验得出计算参数。土工织物与土体的接触面采用Goodman单元，由于土工织物不能承受压力，接触面的法向刚度Kn取大值。所有计算参数见表11.2。

表11.2　有限元计算参数表

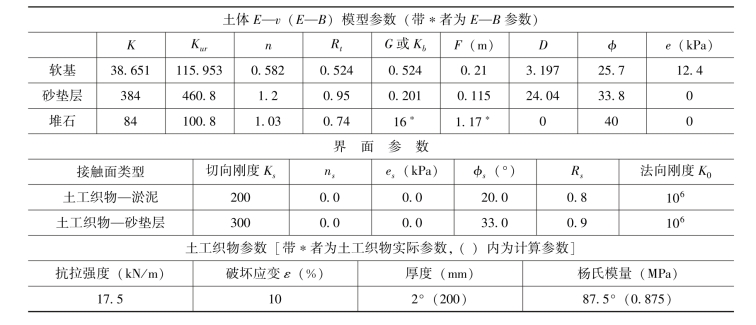
本文对15m软基上抛填4.4m隔堤，进行了堤底加筋与无加筋两种工况的有限元计算，并与离心模型试验结果做了比较。

表11.3　有限元计算与试验结果对比

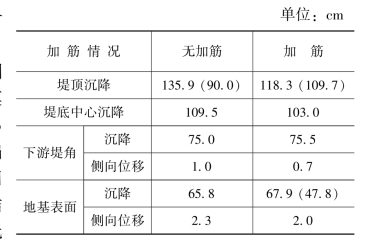
注　（）内为试验值，其余为计算值。

表11.3给出计算及试验所得沉降和侧向位移值，试验值取自1号模型和3号模型，分别为无加筋和加筋情况。由表11.3的对比可以看出，计算值比试验值略为偏大，但在可以接受的范围以内。差别的原因可能与计算中所采用的土体参数是三轴固结排水试验所得的有效强度指标有关，有限元分析得到的结果表示土体完全固结稳定后的状态；而离心试验由于时间的关系，仅模拟了土体的部分固结状态，故其值偏小。