模块式加筋土挡墙的设计优化

6.2.8.1　模块式加筋土挡墙的特点

前面讨论的加筋土挡墙都是针对连续式预制面板而言的，这时，面板为一整体。20世纪80年代中期起，北美出现了一种模块式加筋土挡墙（Reinforced Soil Segmental Retaining Wall SRW），它改变了连续式的面板结构，以大小不等形状各异的独立预制模块堆叠干砌而成。其优点是更加美观，也便于搬运，施工简单，同时经济性好。模块的形状如图6.19（a）所示，厚度一般为150～180mm，高度为80～600mm，长度为150～1800mm，每块块重30～50kg。典型的模块挡墙形式为图6.19（b）。我国如扬州古运河驳岸工程，北京顺义王里仓格栅加筋立交桥，都是这种类型的工程实例[如图6.19（c）]（刘志祥，2000）。

图6.19　模块式挡墙

（a）模块的型式；（b）模块式挡墙典型断面；（c）扬州古运河驳岸工程模块式挡墙（刘志祥，2000）

模块式加筋土挡墙的情况与土工石笼和土工袋堆叠形成的挡墙有类似的特点，因此，本节的内容对石笼挡墙和土工袋挡墙等结构物也可参照使用。

6.2.8.2　模块式加筋土挡墙的计算特点

（1）破坏模式。模块式挡墙的破坏模式除一般加筋土挡墙的破坏模式之外，尚有：①层间滑动；②鼓胀；③顶部倾倒。这些都可认为属于局部失稳现象，如图6.20所示。为此，要求模块间应有足够的摩阻力，以阻止模块间的过度位移。同时，筋材应有足够的抗拉能力，而且筋材布置的垂直间距不能过大，以保证墙体的整体性。此外，要求顶部未加筋部位的高度不应过大，以保证其不发生倾倒和不产生过大的横向位移。

图6.20　模块加筋土挡墙可能破坏模式

（a）水平滑动；（b）倾覆；（c）承载力不足；（d）筋材拔出；（e）筋材拉断；（f）层间滑动；（g）连接破坏；（h）鼓胀；（i）顶部失稳

（2）自稳高度。自稳高度H0系指干砌模块主体能站立不倒的最大高度，在自稳高度范围内，所有模块的重量都作用在底部模块的底面上。对于墙面具有倾斜度ω的情况，应满足式：

式中：MB为底部墙踵Z点右边的模块墙体重对Z的取矩；MA为底部墙踵Z点左边的模块墙体重对Z的取矩。

当ω=0时，自稳高度H0就等于模块墙的高度H。

（3）墙面土压力。墙面土压力与墙高有关，其水平分量的计算如下式所示，参考图6.21：

式中：为土压力的水平分量；为填土水平时墙背上土压力的水平分量；为填土表面附加荷载及活荷载引起的墙背土压力的水平分量；γ为填土容重，kN/m3；H为墙高；δ为土与墙面的外摩擦角；ω为墙面的倾角；Ka为主动土压力系数。

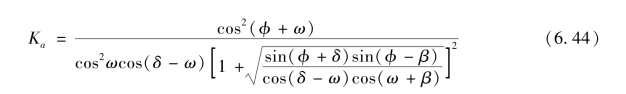
式中：φ为填土内摩擦角；δ的取值，根据王正宏建议，当进行内部稳定计算时取，当进行外部稳定计算时取φ值。

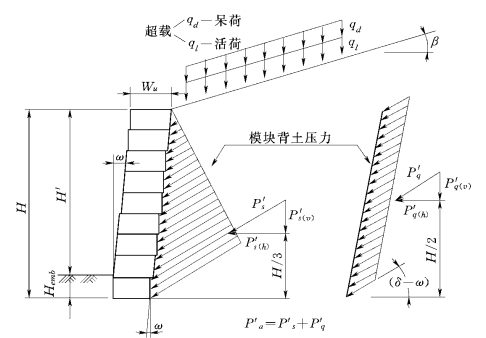
图6.21　内部稳定性验算

6.2.8.3　模块加筋土挡墙的布置

（1）几何形状。模块挡墙形状典型图示于图6.19。模块柱体下设透水性材料的填平层，并与墙后面的竖向排水相连。墙体埋深Hemb（=H-H′），对墙前地面为水平者采用H′/20；对墙前地面为坡面者，采用H′/7；但最小为15cm。

图6.22　模块界面强度试验成果举例

1—带混凝土抗剪键或边挡块的下限（实体、空腔填土……）；2—表面
平整，空腔内填土

（2）模块间抗剪力。模块的形式可在图6.18（a）中选择，当模块形式选定后，模块间的抗剪力应通过试验确定。扬州勘测设计研究院曾研制过这种测试设备，其型式类似于直剪试验。图6.22为一个试验成果的例子。不同型式的模块其抗剪力是有差别的。试验成果可采用直线方程拟合，与一般的抗剪强度公式类似，即

(www.xing528.com)

6.2.8.4　稳定验算

外部稳定验算与一般加筋土挡墙相似，不再赘述。内部稳定验算除要验算筋材的断裂（包括筋材在与墙面连接处的拉断）、筋材的拔出之外，还应验算模块层间的抗滑动能力。上述验算与通常的加筋土挡墙类似。除此外，对模块式挡墙还应进行局部稳定性验算，现分述如下。

（1）模块间的抗滑动验算。对照图6.23，第n层的抗滑安全系数按下式计算：

图6.23　内部抗滑动分析示意

式中：为第n层以上筋材与周围土之间的抗滑力；V（n）为模块间抗滑力；Pa（h，n）为验算筋材高程以上的土压力水平分量。

式中：W′（i，n），W′（β，n）分别为第n层筋材以上墙体和墙顶坡土的重量。

式中：au为模块之间表观最小抗剪力；W（n）为第n层以上模块的重量；λu为模块间峰值抗剪力的表观摩擦角，对于扬州古运河的模块挡墙，测得au=20kN/m，λu=27.5°。

式中：H为自稳高度；γu为模块材料容重；B为模块的宽度（图6.23）。

（2）抗墙面鼓胀（bulging）验算。某层模块向外鼓胀反映了该模块在上、下压力作用下失去了保持原有相对位置的能力。抗鼓胀力由模块间的垂直压力、筋材间距和块间抗剪力等决定。

假设，模块墙体为一连续楔，水平荷载（土压力）连续分布在梁上，绘出该梁的剪力图（图6.24）。该剪力图是将某层n以上从墙顶开始的不平衡力逐一往下累积而得。

1）某一层面的最大不平衡力等于该层以上的水平土压力减去现有的筋材拉力。

2）任一层面的抗剪力按式（6.50）计算。

某层筋材的最大拉力按式（6.50）计算：

式中：Ac（n）为n层筋材在墙上的受力垂直面积，即筋材受力范围在垂直面的投影面积，见图6.25；Dn为受力垂直面积中心处的深度。

3）某层总水平土压力P′a（h）可按式（6.43）计算，但应将式中的H换为筋材以上的高度。

图6.24　验算墙鼓胀的剪力图（土压力视为作用在梁上的连续分布荷载）

图6.25　内部稳定性验算时力与应力

4）抗鼓胀安全系数FSsc（n）应不小于1.5。

如果上述安全系数不满足，应改变筋材的垂直间距或增加筋材的层数来调整。

（3）抗顶部倾倒。这时，对顶部不加筋部位的高度应加限制。为此应验算该未加筋模块柱体的自立稳定性。计算方法比较简单，不再详述。安全系数也应满足不小于1.5的要求。