湖北杨女士上诉被加拿大法庭裁定不予考虑

近年，加拿大Richard.J.Bathurst等人对目前流行的加筋挡墙设计方法的保守性提出了严厉的批评。他们认为当前在北美流行的American Association of State Highway and Transportation Officials（AASHTO）简化法，对加筋挡墙长期运行所需的筋材数量估计得过于保守（R.J，Bathurst et，2005）。他们对现存的加筋挡墙运行良好的多个实例进行了收集和分析，结果认为，为满足长期稳定需要的加筋量仅为上面流行方法要求的一半左右，甚至有的仅为要求的1/8。导致保守的原因除过低估计设计的峰值摩擦角之外，筋材上的荷载估计得不准确也是重要的原因。为此，采用加筋土挡墙的筋材应变实测资料反算筋材上的荷载，并提出了新的计算筋材荷载的方法。在由实测应变计算荷载的转换过程中，筋材刚度的确定十分重要，Bathurst选用蠕变试验应变为2%所对应的刚度值。

6.2.7.1　新方法的实质

Bathurst等人从北美、欧洲和北欧现存的加筋挡墙现场精心选择了埋设有监测仪器的数十个例子，并结合在加拿大Royal Military College of Canada（RMC）进行的足尺试验，提出了一个对复合加筋材料（component reinforcement materials）可以接受的准则以及粒状回填土的可靠强度资料。而评估现行方法的保守性和建立一个新设计方法的基本问题乃是对加筋层中的荷载作出可靠的估计。

根据所研究的实际资料而进行的最优筋材荷载的估计值，可以得到梯形的筋材荷载分布，它比目前假定的三角形分布更为精确。

6.2.7.2　实例分析

在20个实例（包括35个不同墙断面）中，筋材采用聚丙烯PP，高密度聚乙烯HDPE和聚酯PET的土工织物和（或）土工格栅。其拉力强度为12～200kN/m，刚度（在施工结束时）为43～7400kN/m（当应变为2%），筋材的垂直间距为0.3～1.6m，墙面倾角为0～27°，大部分为8°，墙高为3.0～12.6m，填土表面荷载相当于高5.3m土柱。由三轴和直剪试验求得的峰值内摩擦角为39°～49°（平面应变为42°～57°），墙后回填采用干净的砂砾石，挡墙的地基坚硬。

挡墙整体（global）安全余量定义为筋材承载能力的总和（R称为抗力）与加筋层总水平向土荷重（D称为需求）的比值。抗力与需求之比（RD）可表示为

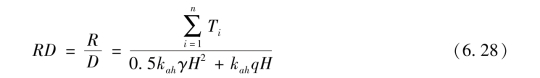
式中：Ti为筋材承受的荷重；γ为墙土容重；q为土面上均布荷载；kah为主动土压力ka水平分量。

式中：φps为土的平面应变峰值摩擦角，若无平面应变资料则由填土的三轴或直剪试验求得；ω为墙的倾角；δ为墙与填土之间的界面摩擦角（根据AASHTO，假设δ为零）。

图6.14为30个工程的比值出现频率直方图。由图6.14看出，按AASHTO计算的RD一般都比实际RD为大，在30个实例中，90%以上的设计过于保守（比值大于1.0），20%的实例，其比值甚至达到4，仅有10%的加筋工程，其设计值小于实际值，即使如此，这些墙的工作状态依然良好。

图6.14　应用AASHTO方法的保守程度（Allen等，2002）

仔细分析后表明，只要有AASHTO法算得的筋材一半就可以满足安全要求了。引起过于保守的原因，一方面是所采用的摩擦角不是平面应变的（φps），而是三轴或直剪试验的资料（φdes），另一方面，是在AASHTO简化方法中筋材上荷载的预测模型过于保守。

6.2.7.3　建议的新方法——“K—刚性法”（K—stiffness Method）

上节中，已对加筋挡墙内部稳定核算中筋材作用荷载的计算，采用现行的AASHTO简化方法存在的缺陷作了概括的说明，Bathurst等根据“工作应力原理（Working stress Principles）”发展了一个新的设计方法。筋材所受的荷载可由在工作荷载下所测得的应变发展出来，这是一种基于经验的设计方法，称为刚度法。

（1）影响最大筋材荷载Tmax的主要因素。

1）墙高和附加荷载。

2）加筋土的整体和局部刚度。

3）墙面的刚度和墙趾的约束引起的侧向移动的阻力。

4）墙面斜角。

5）土的强度和应力应变（模量）特性。

6）土的单位重。

7）筋材的垂直间距。

应当注意，在AASHTO简化方法中，没有考虑第二项和第三项的影响。尤其是没有考虑筋材刚度的大小对筋材荷载大小和分布的影响。这些影响在物理试验和数值模拟中已得到证实。

（2）K—刚度法的计算公式。在K—刚度法中，这些关键因素对某一加筋层“i”的最大荷载的计算公式可表示为

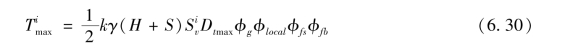
式中：k为侧向土压力系数；γ为土的容重；H为墙高；S为均布荷载q的当量高度，（即S=q/γ）；Si

v为相邻筋材层的间距；Dtmax为荷载分布系数；φg，φlocal，φfs，φfb为考虑整体和局部筋材刚度的作用，面板刚度和倾斜度等的影响因素。

Dtmax称为经验的筋材荷载分布参数，等于Tmax/Tmxmx，它是深度的函数，取决于筋材的特性、荷载沿筋层的分布，以及地基的条件，在此表示为墙顶以下归一化深度的函数，见图6.15，包括填土S的作用，其值在0≤Dtmax≤1.0范围内的变化。这个分布还可以进一步简化，设Dtmax在墙高的20%的底部，其值为1.0。Allen和Bathurst（2003）指出，荷载的分布可能是整体筋材刚度加局部筋材刚度的函数。

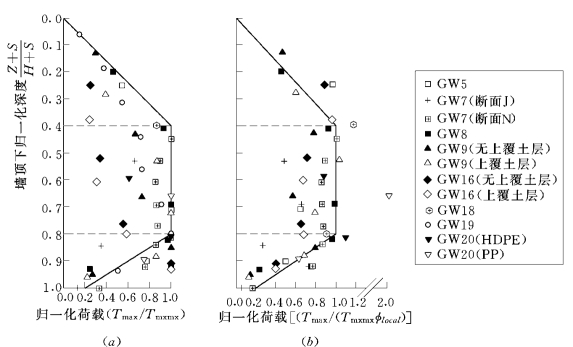
图6.15　由应变测值推算的归一化筋材荷载与归一化深度（墙顶以下）的关系

（a）归一化荷载（Tmax/Tmxmx）；（b）归一化荷载[Tmax/（Tmxmxφlocal）]

参数φg系整体刚度系数，它能考虑筋层的刚度和全墙高的筋层间距的影响，其一般的形式为

式中：Sg为整体加筋刚度；α和β为常数；Pa为大气压。

式中：J平均是在全墙高度上所有加筋层“n”的平均拉伸刚度；Ji为单个加筋层的拉伸刚度（以每单位长度墙的力计）。

φlocal为局部刚度系数，它考虑筋材层的相对刚度，所有筋材层的平均刚度，可表达如下：

式中：Slocal为加筋层“i”的局部加筋刚度，。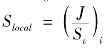

式（6.30）中的参数φfs（墙面刚度因素）和φfb（墙面倾斜因素）乃是考虑墙面刚度和墙面倾斜的影响，对给定的墙，它是常值。

在初步设计中，对面板刚度系数有如下的建议：

（1）φfs=0.35～0.5　对模块和混凝土面墙（刚性面墙）。

（2）φfs=0.5～0.7　对预浇混凝土墙。

（3）φfs=0.7～1.0　对其他类型的墙面（柔性墙面如包裹面、焊丝或格宾面墙等）。

上述建议值对不同的资料来源可能有不同的值。

在所建议工作应力法中，墙面斜度对最大筋材荷载的影响可用一经验墙面倾斜系数来表达：(www.xing528.com)

式中：Kabh为在考虑墙面倾斜情况下主动土压力系数的水平分量；Kavh为墙面垂直时的主动土压力系数的水平分量；d为墙面倾斜常数，当ω→0时，Pfb→1，d=0.25，该值可作为K—刚度法的无偏估计值。

6.2.7.4　K—刚度法与AASHTO简化法的比较

K—刚度法对于土工材料加筋墙的精度示于图6.16，比AASHTO简化法（图6.17）有所改善。

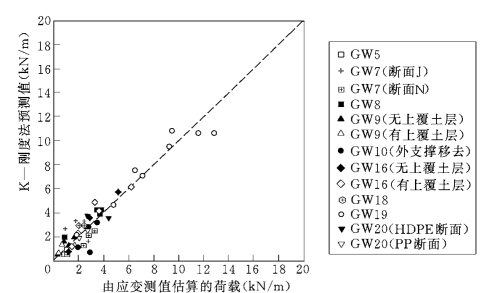
图6.16　加筋土挡墙中加筋层的荷载实测值与预测值（K—刚度法）的对比（Allen等，2003）

类似地，K—刚度法比简化法在加筋土墙中荷载的分布方面也有改善，如图6.18所示。该法是对3种不同的墙面作出比较的。

K—刚度法比AASHTO简化法的改善还可从筋材作用荷载的量测值和预测值的比值以及离差值的分散程度（the spread in the bias values）得到定量的验证（表6.1）。

6.2.7.5　加筋挡墙极限状态中土体破坏的考虑

目前的设计方法均集中于筋材的断裂或拔出作为挡墙内部稳定的关键极限状态。但是作为这种挡墙的重要部分之一，即回填土本身，却没有引起太多的关注。众所周知，土工材料的破坏应变远比土的破坏应变大。因此，防止筋材的破坏，并不能保证加筋挡墙不被破坏，因为破坏可能由于回填土的破坏而引起。可见，在结构物设计寿命期防止筋材的过大应变（此时筋材不一定破坏），仍应当是任何工作应力设计方法（Working stress design method）的目的之一。

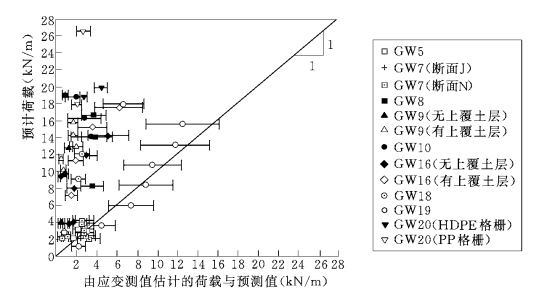
图6.17　从实测应变估计的荷载值与预测值（AASHTO简化法）的比较

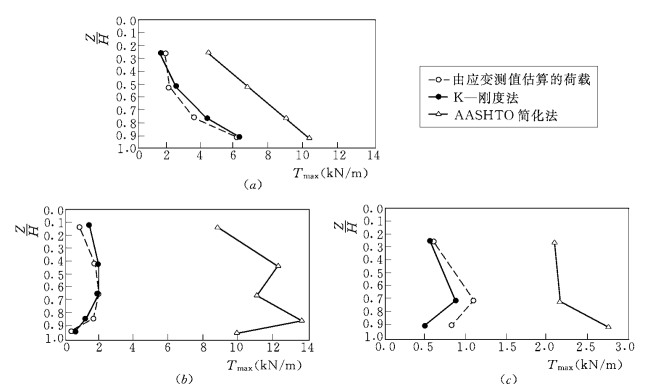
图6.18　土工合成材料加筋墙中筋材层Tmax预测荷载及其分布与量测值的对比

表6.1　K—刚度法与AASHTO简化法的统计特征比较

注　Tmax为加筋层的最大荷载；Tmxmx为墙中所有加筋层的最大荷载；COV（离散/离散均值）×100%的标准差，离差值的COV越低，精度就越高。

土的破坏定义：当土中存在连续的或近似连续的区域，在该区域中土的剪应变超过峰值强度对应的应变值，则认为土发生了破坏。专门进行的在均布荷载作用下挡墙试验的破坏中已观察到连续剪切区的存在。一旦土进入破坏，则墙也就破坏了，且达到了内部强度极限状态。Bathurst等人在RMC进行的足尺试验中观察到：土的破坏是先于筋材断裂的。土的破坏的征兆表现在墙面突然发生向外大变形，墙面后的土直接下沉，同时筋材应变增大，在某些实例中，附加荷载的进一步增加将导致筋材的断裂和墙的崩坍。

由此可知，在加筋挡墙的设计中，除了筋材的断裂、拔出和过大应变外，墙后填土的破坏也应作为一种极限状态在设计中加以考虑。

上述的Bathurst的研究成果再次证实了一个重要的观点，即在加筋土结构的稳定性分析中，不应仅仅关心筋材与土界面上的效应，而且应当把加筋土作为一个整体考虑，或者说，应当把眼界从仅仅在界面上的加筋机理上扩展到包含复合加筋土体中土体的作用和影响上，把土体的破坏也作为复合加筋土体的一个破坏状态加以分析，这是目前加筋土体性状研究中的一个新倾向。实际上，这个新倾向也意味着加筋不仅增强了界面处的阻力，而且也间接地增大了土体的强度。这是与“加筋机理”中的“间接影响带”观点一致的。

陈永辉在他对加筋土体设计理论的研究中，提出了复合加筋土体的三种破坏状态：即断裂型破坏（筋材被拉断）、摩擦型破坏（筋材被拔出）和变形过大型破坏（当土体的侧向容许应变小于筋材的极限应变时，就可能发生）。这里所指的“变形过大型破坏”就与上述的土体极限状态破坏有相似之处。“此时，复合土体中的土体已发生破坏，从而导致整个复合土体不能承受更大的荷载。发生此种类型破坏时，筋材应未发生断裂，也未与土体发生完全错动，因此，在极限情况下，筋材仍与土体协调变形”。

对于这种破坏情况，陈永辉建议了复合加筋土体的设计计算方法，简介如下。

6.2.7.6　筋材应变过大时，加筋土体破坏的计算

当复合加筋土体处于变形过大的极限状态时，筋材的拉伸应变εg等于土体的侧向容许应变ε3a，此时筋材受到的单宽拉力为

式中：Eg为筋材的拉伸模量；ε1a为土体竖向容许应变；μ为土体的泊松比。

另一方面，我们来讨论未加筋土体和加筋土体的竖向极限荷载的情况。对未加筋土，按摩尔—库仑理论，竖向极限荷载σ1f有

当土体加筋后，复合土体中的土除受到外力外，还受到筋材的摩阻作用，这种摩阻作用可以用摩擦等效附加应力的σadsf来表征，如果认为复合体达到极限状态时，复合体中的土体也达到极限状态，于是复合体的摩尔—库仑强度准则可表示为

式中：kp为被动土压力系数，kp=tan2（45°+φ/2）。

σadsf为极限状态下摩擦等效附加应力，对于加筋复合体单元中只有一层加筋材料时

式中：Tu为复合体极限状态下筋材受到的单宽拉力，kN/m；s和t分别为复合体单元中土体的厚度和筋材的厚度。

对加筋土变形过大的极限状态，竖向极限荷载有σ1f有

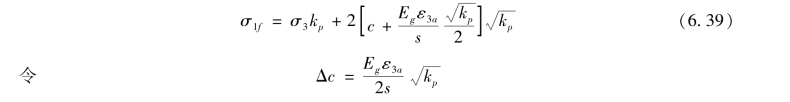
把上两式相比可知，土工材料的加筋相当于增加了一个凝聚力Δc，而φ不变。欲判断复合加筋土体中的破坏属于那种类型，可进行如下讨论。

（1）筋材断裂的极限状态时，筋材所受的单宽拉力Tu应等于筋材的单宽抗拉强度，即Tu=Tf。但是Tu＜Tf，则筋材不会被拉断，可能发生拔出破坏，又若Tu≥Tf则筋材会被拉断，不会发生拔出破坏。由此，即排除了一种可能性。

（2）把上一步骤中判断出的可能破坏型式与第三种变形过大的破坏作比较，即可判定哪一种类型为控制性破坏类型。

（3）假定上述的第二种破坏类型被排除，将剩下的第一种型式与变形过大型式作比较。

这时只需计算两种极限状态时筋材受力大小，即Tu=Tf（第一种类型）和Tu=ε3aEg（第三种类型）。

当ε3aEg＞Tf时，发生的是断裂破坏；当ε3aEg＜Tf时则发生变形过大型破坏。

（4）对于排除了第一种破坏类型的情况，只需进行第二种与第三种类型的比较，这时第二种极限状态下，筋材的单宽拉力为

式中：σ10为最小竖向主应力。

若已知σ10，可直接与ε3aEg比较进行判断。若σ10未知，则可通过σ3判断。两种类型的临界围压为

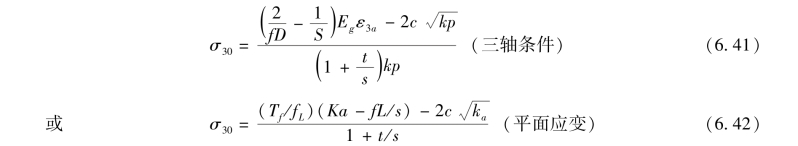
当σ3＞σ30时，试样发生变形过大型破坏；当σ3＜σ30时，试样发生拔出型破坏。其中σ10，σ30为两种破坏类型的临界围压，在加筋上结构的设计中，应保证使上述三种的破坏型式不会出现（陈永辉，2006）。