加筋土的拉拔和直剪试验优化

5.6.2.1　拉拔试验和直剪试验的简介

加筋材料与其周围土体之间的界面特性参数是加筋土研究和应用中最重要的设计指标之一。拉拔试验的装置参看图5.29（a）。在试验装置上下盒之间的试样中间，放置一水平的土工加筋材料（如土工格栅），筋材的一端自由，一端受拉。

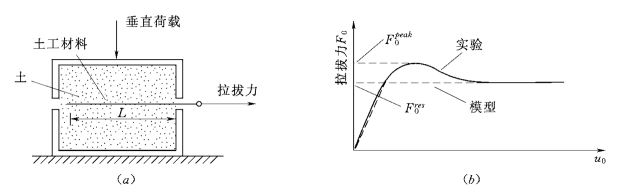
图5.29　拉拔试验原理和试验曲线

（a）拉拔试验原理；（b）拉拔力—位移曲线

根据拉力与筋材位移的值，绘出拉拔力与位移关系曲线[如图5.26（b）]。由此可得表观（apparent）摩擦系数μ*：

式中：F为拉拔力；B为试样的宽度；L为筋材埋入土中的长度；σv为垂直应力；τ为平均连接剪应力。

相应于拉拔力的峰值和残余值，可以得到两个μ*值。

直剪试验为大家所熟知，其原理如图5.27（a）。试验可得如图5.30（b）中的成果，其斜率即为摩擦系数。

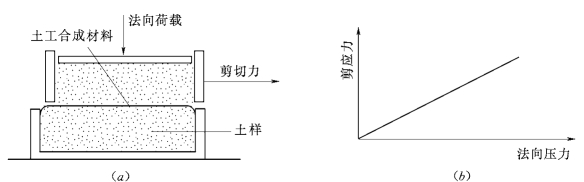
图5.30　直剪试验原理和试验曲线

（a）直剪试验原理；（b）典型的试验成果

式5.7和式5.8是类似的，虽然两者的剪应力的定义稍有不同。对比本节所述的直剪试验和上节所述的三轴试验，两者是有所区别的。图5.31（a）和图5.31（b）所示的分别为加筋土三轴试验和直剪试验的原理示意。

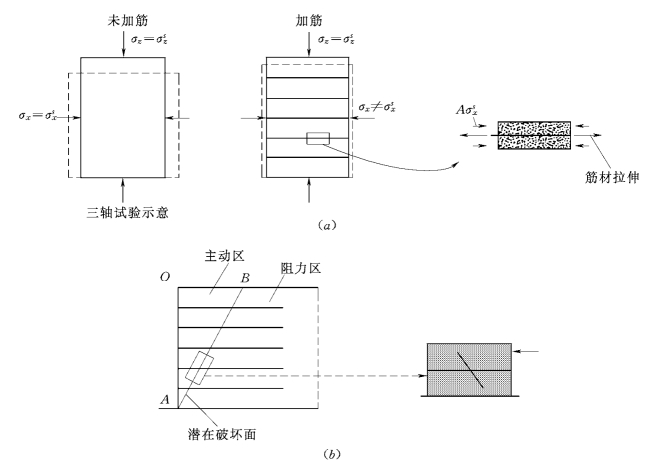
图5.31　三轴试验与直剪试验原理的比较

（a）三轴试验图示意；（b）直剪试验分析

Sawicki认为，从图5.31看出，直剪试验中应力状态与三轴的不大一致。如果要发生如图5.31（a）的滑动面，则穿过滑面AB的所有筋材的相交点均应进入塑性状态，直至刚性滑楔OAB开始移动。其过程如下：在筋材中产生拉应力，筋材的强度损失，筋材的拉伸塑流和土的摩擦剪切表明了破坏的特征。然而，直剪试验中发生的一系列情况不同于加筋土的原理。在直剪开始剪切前，筋材受压，然后沿固定面的剪切改变了试样的应力分布，当应变较大时，筋材变成轻微伸长，这就是土的破坏了。但是筋材并未因拉伸而破坏。可见，这不是加筋土的典型破坏机理。由此看来，直剪试验的结果不宜用于解释加筋的原理，也不宜在此基础上建立任何理论模式（Sawicki，2000）。但是，它可用来求得土与筋材之间的摩擦强度（Palmeira，2007），因此仍有用处。而拉拔试验不仅可以求得两者的摩擦角，而且可以获得土与筋材之间的咬合力和剪切全过程中各个剪阻分量变化的信息。因此，国外的许多研究者都十分重视拉拔试验的研究，对它的影响因素和如何用于现场条件进行了深入的讨论，下面将做简单介绍。

5.6.2.2　直剪试验和拉拔试验的成果

马时冬（2004）对不同的筋材和加筋层数进行了直剪试验和拉拔试验以了解加筋土的加筋效果，其成果如表5.3所示。从表5.3中看出，加筋的效果与筋材的特性和土的特性有关。业已清楚，筋材与土的接触面的摩阻力σ大小与筋材表面的糙度有关，且剪切带的发展及其厚度也与糙度密切相关。此外，筋材的糙度越大，筋材与土之间嵌锁作用（即咬合力）也越强，摩阻力也越大。

表5.3　直剪试验与拉拔试验成果简表

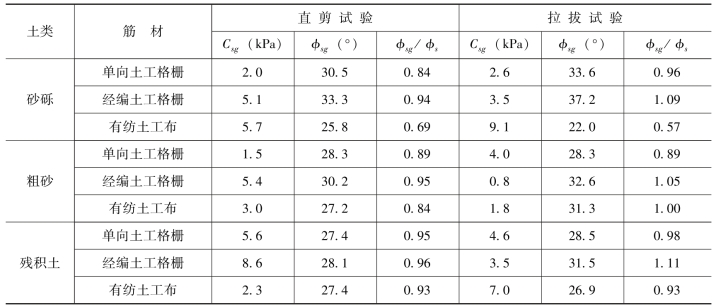
注　φsg/φs为接触面的摩擦角和土的内摩擦角的比值。

摩阻力的大小还与土的粒径有关，粒径越大，则加筋土的强度一般也越大，因为当加筋土被剪切时，邻近被动员起来的颗粒也越多。

吴景海等（2001）曾进行过不同土工加筋材料与砂等介质接触面的直剪试验，成果如表5.4和图5.32所示。(www.xing528.com)

表5.4　土工合成材料与砂的直剪试验成果（峰值强度）

由此可见，直剪试验可以测得接触面摩擦角的值，而且规律性较好。在本例中，筋材与土的接触面摩擦角小于纯砂的摩擦角。但总的说来，直剪试验得到的界面特性资料，不如拉拔试验充分和清晰，尤其当法向压力较低时。图5.33分别示出了经编土工格栅与砾石的直剪试验和拉拔试验成果。可看出，直剪试验求得较低的摩擦角和较高的黏聚力，而拉拔试验则摩擦角较高，而黏聚力较低。这可能与直剪试验的约束有更大关系。

拉拔试验是一种研究界面特性的更为普遍和重要的试验方法，它是在筋材两面均与土接触的条件下进行的，因此与直剪试验的单面与土接触的条件不同，但两者可望建立一定的关系。鉴于拉拔试验对界面特性和设计参数的重要性，下面将有专门的一节（5.6.3）对拉拔试验过程中位移与应力情况进行较为详细的分析。这里先介绍一些拉拔试验成果。

丁金华（2006）最近对塑料土工格栅与膨胀岩碎石土的加筋土进行了大型拉拔试验。试验采用长江科学院DHJ60叠环式剪切仪中进行（已如上述），环与环之间摩擦力很小。加筋材料采用单向高密度聚乙烯（HDPE）土工格栅。对拉拔的全过程进行了格栅不同部位的位移量测。可以看到，试验分为三个阶段：第一阶段是施加拉拔力后，筋材尚未被拉动。此时的摩擦力应为静摩擦力；第二阶段，当拉拔力增大时，筋材被拉动，且从夹具装置端向筋材深部逐渐延伸，直至筋材的末端也产生拉拔位移，这时的剪阻力为动摩擦力加咬合力，该咬合力是在格栅与土产生一定相对位移后逐渐显露的；第三阶段是筋材整个被拉动，筋材与土之间的相对位移呈匀速发展，此时拉拔力也达到峰值，并有减小的趋势，如图5.34所示。图5.31中所示的OA、AB和B点以后的3段，即反映上述的3个试验阶段。从图5.34中还可以大致估计筋材进入匀速拉动时的变形约为10mm左右，相当于1.5%应变。

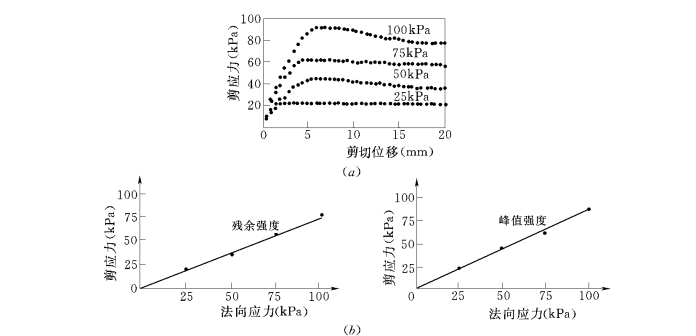
图5.32　砂与土工合成材料直剪试验的典型曲线（吴景海，2001）

（a）剪应力与剪切位移关系曲线；（b）抗剪强度线

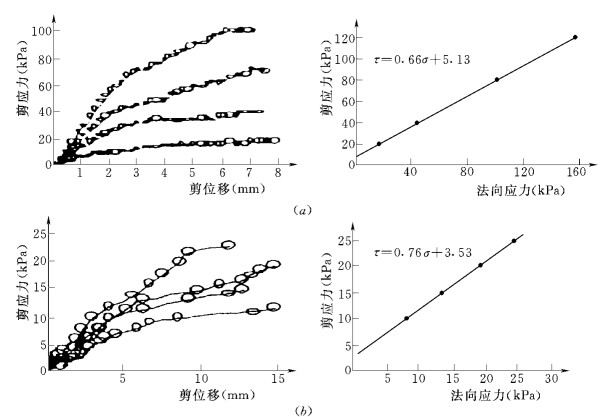
图5.33　土工格栅拉拔试验成果和直剪试验成果（马时冬，2004）

（a）经编土工格栅与砾石的直剪试验；（b）经编土工格栅与砾石的拉拔试验

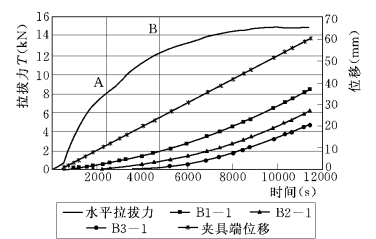
图5.34　HDPE50格栅不同部位的位移过程线（σn=200kPa）

5.6.2.3　拉拔试验与直剪试验的关系

众所周知，拉拔试验和直剪试验都可以模拟土与筋材之间的相互作用，并求出有关的计算参数。但是一般认为，直剪试验不能很好模拟筋材的受力特性，从而推荐用拉拔试验等来研究界面特性和确定摩擦系数。同时，由直剪试验求出的摩擦系数往往小于拉拔试验的值，尤其对密砂试样（Zhenggui Wang and Werner Richwien，2002），有人认为，这与砂土的剪胀性和筋材的糙度有关，如果考虑这两个因素，则可以建立拉拔摩擦系数与直剪摩擦系数的关系。

对于拉拔试验，拉拔摩擦系数f*可表达为式中：F为拉拔力；σm为平均法向应力；b和L为拉拔试验的宽度和长度。经过理论分析，导出了下列的拉拔摩擦系数与直剪摩擦系数的关系如下：

式中：f为直剪摩擦系数；ν为泊桑比；ψ为剪胀角，有人建议对于密砂ψ=25°～26°；G为砂的剪切模量；E为变形模量。

此外，图5.35中的φds为直剪摩擦角。

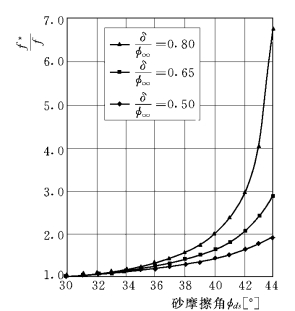
图5.35　不同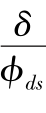下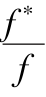与φds的关系

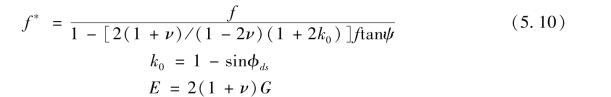
由式（5.10）可知，ψ对该式有强烈的影响，当ψ=0时，f*=f。同时，还应注意，式（5.10）中，若分母中[2（1+ν）/（1-2ν）（1+2k0）]ftanψ≥1.0，则该式失效，这相当于界面非常粗糙，或剪胀角十分大的情况。然而对大多数的砂，ψ角不大于15°，因此式（5.10）对大多数情况还是适用的。

图5.35中表示出了（f*/f）—φds和ψ在不同筋材表面糙度下（即不同的δ/φds值，δ为界面摩擦角）的计算成果，其中，设ν=0.33，φds=39°，δ=30°，ψ=15°，于是按式（5.10）可得：f*=1.91，而实测值为2.01～3.00，表明两者具有可比性。

上述关系表明，虽然两者尚需进行更多验证，但探究用直剪试验估计拉拔试验成果的可能性还是存在的。