塑料排水带地基的固结沉降及强度增长分析

4.9.2.1　排水带地基的固结计算

排水带地基的固结是借用砂井地基固结理论来计算的，所以下面仍以砂井地基的固结理论来阐述。应用于排水带地基时，只需把排水带的截面积换算成砂井的等代面积，便可以计算。

一般砂井地基的平面布置有正方形和梅花形两种，如图4.41（b）、图4.41（c）所示，在大面积荷载作用下，设每个砂井（直径为dw）为一个独立的排水系统[图4.41（d）]，每根砂井的影响范围分别为正方形和六边形[图4.41（b）、图4.41（c）]。为简化起见，每根砂井的影响范围用等面积圆代替，其等效直径为de：

式中：de，l分别为等效直径和布置间距。

早在20世纪30年代Rendulic（1935）等人就开始对砂井体系的固结进行了研究，Barron于1948年总结以往的经验和成果，提出了等应变和自由应变两种极端情况，不考虑井阻和涂抹作用的理想井的固结理论和等应变条件下，考虑井阻和涂抹作用的非理想井固结理论，此理论至今仍然被视为经典的砂井固结理论。随着竖向排水固结应用的发展，特别是塑料排水带的出现，不考虑井阻涂抹作用的理想井理论在实用中已感到许多不足，因此，Yoshikuni（吉国洋）（1974）和Hansbo（1981）又提出了考虑井阻涂抹作用的比较严密的非理想井固结理论。根据近年来理论研究与工程应用的结果认为（谢康和，1981），Barron的非理想井固结理论与工程实际相比偏于保守，Hansbo的是近似解，Yoshikuni的精确解非显式表达，不便于工程计算。谢康和在总结上述理论研究成果的基础上，结合工程应用实际，提出新的非理想井固结理论解，这一理论解物理概念清楚，公式表达比较简明，参数易于选择，计算方便，与经典的Barron固结理论相似，兹介绍如下。

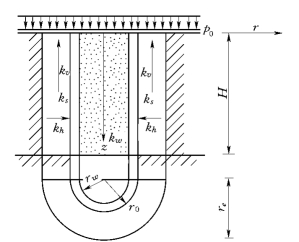
图4.44　砂井固结理论分析

理论分析时可取一单井，其排水条件简化为如图4.44所示：H为软土层的厚度，单向排水时为最大的排水距离，打穿软土层的砂井（或排水带）为其长度；kh，kv分别为软土层的水平向和竖向渗透系数；kw，ks分别为砂井井料和涂抹层的渗透系数；rw，rs，re分别为砂井、涂抹区和砂井有效影响范围的半径；p0为地表均布荷载；r，z分别为径向和竖向坐标。分析时，假定荷载p一次瞬时施加，砂井与地基土等应变条件成立。根据这样的荷载和排水固结条件下的固结理论解，对于一次瞬时加荷，砂井打入深度内地基的总平均固结度为

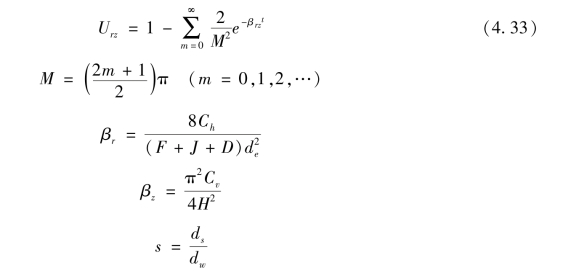
式中：βrz为固结指数，βrz=βr+βz；βr、βz分别为径向、竖向固结指数；F与井径比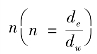的函数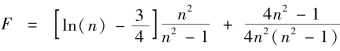，；J为涂抹因子，J=；s为涂抹比；ds，dw分别为涂抹区和砂井区的直径；D，G分别为井阻因子函数和井阻因子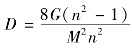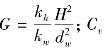，，，Ch分别为竖向和水平向固结系数，m2/s。，。

工程实际应用时，对于打入深度范围内的平均固结度，可以简化为

其中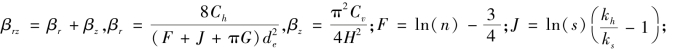：或。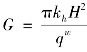

井阻因子G和涂抹因子J中的kw，qw，ks，s不易准确确定。由室内测定的结果与工程实际中真实参数差距较大，因此在工程上采用试验结合经验值。根据CTAG02—97《塑料排水带地基设计规程》中的建议，排水带的通水能力（qw）可取排水带产品室内测定值的， 当打入深度L＜10m，取，L＞20m取，L=10～20m之间取；涂抹比s取1.5～4，施工扰动小的（压入式施工）取低值，扰动大的（振动打入）取高值；渗透系数比k k hs可取1.5～3，非均质粉质黏土取3～5，具有明显的粉土、细粉砂土微层理结构的可塑性黏土取5～8。

简化式与精确解相比，误差小于10%，一般可满足工程应用的要求，这一理论解的表达式还可以转化为理想井和无砂井情况固结度的计算。

（1）令式中G=0，s=1，可转化为理想井情况。

（2）令式中G=0，可转化为无井阻情况。

（3）令式中βrz=βr可转化为不考虑竖向排水的情况。

（4）令式中βrz=βz可转化为无砂井的一维固结理论计算式。

对于一级或多级等速加荷情况平均固结度的计算如图4.45所示。

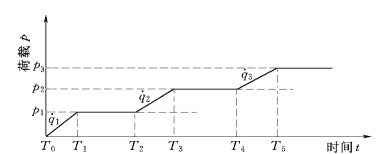
图4.45　多级加荷进程

理论解的平均固结度简化式为

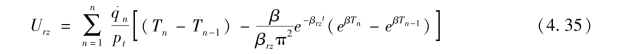
式中：pt为与多级荷载历时t对应的荷载，pt=∑Δp；q.

n为第n级荷载的加荷载速率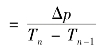，；Tn，Tn-1分别为第n级荷载加荷的终点和始点的历时（从零点计起）；t为所求固结度的历时，所求的固结度是对该时刻对应荷载而言，t应大于Tn，当Tn-1＜t＜Tn时，式中Tn应改为t；n为加荷的分级数。

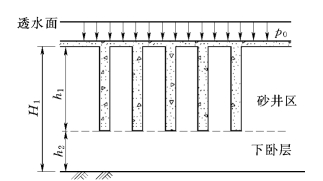
图4.46　砂井未打穿固结土层示意

图4.46所示为砂井未打穿固结土层的情况，即砂井仅打入部分土层，另一部分为不含砂井的下卧土层。显然，这种情况的排水边界条件与砂井完全打穿的情况或一维固结情况均不一样。经分析研究，砂井这部分土层的固结度与按不考虑下卧层影响求得的固结度，两者相差不大。因此，这里仅给出下卧土层的固结度的计算公式，即

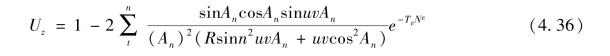
其中

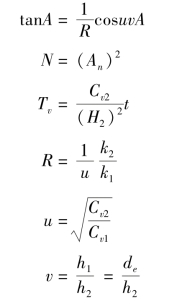
式中：An为式（4.36）的根方程的根，可通过试算求得。请注意，A是多根的；h1，h2，de分别为砂井的打入深度，下卧层的厚度及有效影响直径；k1，k2分别为砂井区土层和下卧区土层的渗透系数；Cv1，Cv2分别为砂井处理区土层的、竖向和下卧土层的固结系数。

必须指出，对于不打穿固结软土层的情况，砂井区与下卧软土区两者的固结速率相差悬殊，不宜用厚度加权平均的固结度来分析地基的沉降。在分析基底沉降时，应按式（4.34）和式（4.36）分别计算出砂井区和下卧软土区的固结度，分别用两区计算得到的最终沉降值来分析。

必须说明，上述固结度的计算式（4.33）～式（4.36）等都是建立在堆载预压（正压）条件下推导得到的，应该只适用于正压排水固结条件的计算。对于真空预压（负压）条件的固结计算是否适用，值得进一步探讨。根据工程实例和室内压缩试验的结果，在同等荷载条件下，真空预压的固结速率和沉降都比堆载预压的大，压缩系数和固结系数也是真空预压的比堆载预压的大。因此，真空预压的固结和沉降计算应与堆载预压条件下的有所不同。然而，真空与堆载两者的排水固结边界条件，除了正压和负压之外都是相似的。因此，建议真空预压（负压）条件下的固结计算仍可用式（4.33）～式（4.36）计算（Mohamedelhassan.E，2002），但是其中固结系数（Cr，Cv）宜用负压条件下室内试验的测定值，一般情况下它比正压固结系数大。

4.9.2.2　井阻和涂抹作用对固结的影响(www.xing528.com)

（1）井阻对固结的影响。井阻因子是影响排水体地基固结的一个重要因素。根据非理想井固结理论，井阻因子愈小，固结的效果愈好，反之则差。根据对某一特定的地基土和排水带打入一定深度的情况下，井阻因子G对地基固结度Urz的影响的研究结果（塑料排水带地基设计规范，1997），当G＜0.1时，井阻对固结效果影响甚微，接近于理想井的固结效果，故可忽略；当G=1时，井阻对固结的影响显著增大，会明显降低地基的固结度；当G＞10时，严重影响地基的固结效果，逐渐趋于无排水体地基（天然地基）的固结。竖向排水体中砂料的渗透系数kw和塑料排水带的竖向通水能力qw以及打入深度H是影响井阻因子大小的主要因素。在某一深度下，竖向排水体的渗透系数或塑料排水带的通水能力过小，将会影响井阻因子增大，导致排水带（井）排水不畅，降低固结效果。因此，设计时，对于某一深度的竖向排水体，必须要求具有足够的通水能力，尽量降低井阻因子，以保证具有良好的固结效果。

确定合理的井阻因子G的关键，取决于竖向排水体在地基原位条件下的实际通水能力。Koerner和Miura等人根据工程原位测试和反分析结果认为：由室内试验测定的排水体产品的通水能力，经过储运、施工中损伤和在地基原位条件下，侧压力的作用使产品的芯带及滤膜产生弹性及蠕变变形，同时，物理和生物环境的改变以及打入排水体时压缩弯折等的影响，会产生较明显的衰减。因此，确定井阻因子G时所用排水体通水能力qw不应是试验测定的产品通水能力值，而是原位条件下的实际通水能力q′w。

其中的折减安全系数FS，是反映上述各种因素对通水能力的影响。根据Koerner（1994）的建议：FS值约在1.5～9。如果在打入排水体中产生扭曲，还要增加一附加安全系数FS=1.0～4.0。Miura等人（1993）通过4座堤坝的反分析，得出地基原位条件的通水能力为初始值的。根据我国12个工程实例反算的结果，FS=2.7～12.9。因此，建议采用概率分布比较集中的中值，即FS=4～6，并按其打入深度和质量好坏分别取高值和低值。按打入深度不同，当L＜10m，FS=4；L＞20m，FS=6；L=10～20m，FS=5。

井阻因子G可按式（4.38）计算：

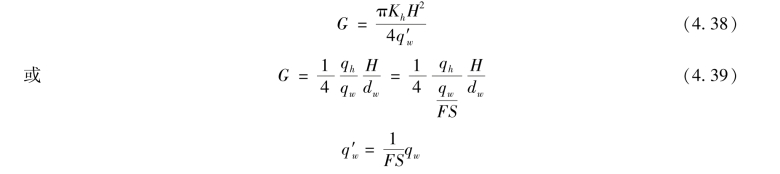
对于塑料排水带式中：kh为地基土的水平向渗透系数，cm/s，由原状土用水平向渗透试验测定，如无试验资料时，对于淤泥质土可取kh=（3～5）×10-7cm/s；qh为单位梯度下地基土中水流入竖向排水体中的流量，cm3/s，用qh=khπdwH求得；q′w为竖向排水体在地基中实际的通水能力（或称竖向渗透能力），即单位梯度下水流通过排水带截面的流量，cm3/s；qw为排水带产品试验测定的通水能力，cm3/s；H为排水带或竖向排水体打入深度；FS为折减安全系数。

设计时，选用塑料排水带的通水能力qw应尽可能降低至可忽略井阻对固结的影响，宜取井阻因子G≤0.1为标准，即令

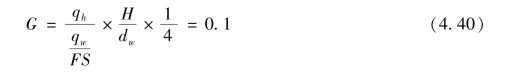
对于打入不同深度的塑料排水带产品的通水能力qw，应满足式（4.41）的要求

（2）涂抹对固结的影响。涂抹作用主要是由于施工对地基土扰动造成的。涂抹的影响范围及对土渗透性能的改变则与施工所用的导管大小、形状和打入的动力方式（静压或振动）及操作的方法等有关。常用导管的平均直径往往比排水带的等值直径大一倍以上，所以常形成具有一定范围的涂抹区，同时涂抹区内扰动后的渗透性能也比地基土明显降低。因此，涂抹作用对固结效果的影响是客观存在而不可忽视的。涂抹作用对固结效果的影响可用涂抹因子J来表示，即

然而，定量考虑涂抹对固结的影响程度或涂抹因子的大小是一个困难的问题，因为涂抹区的范围及其渗透系数难以直接测定，迄今为止，尚未见到测定的结果。因此，涂抹因子中的涂抹比λ和渗透比，只好借助工程实践经验和实测反算的结果来求得。根据Hansbo（1984），Begardo（1990，1993），Miura（1993）等人的原位实测结果，建议如下。

（1）涂抹区的范围与施工机具动力的形式和导管的大小和形式有关，涂抹比的范围约为λ=1.5～4。导管较大，振动打入者，取大值；导管较小，静力压入者，取小值。

（2）涂抹区扰动土的渗透性比值与地基土的结构和性质有关，高塑性均质黏土，=1.5；非均质含粉质土，；非均质并具有明显的粉土或细砂微层理结构的可塑性黏土，。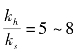

当无试验资料时，可取渗透系数比计算，均质高塑性黏土取低值，1.5～3，非均质粉质黏土取3～5，非均质并具有明显的粉土或细砂微层理结构的可塑性黏土取5～8。

当J≤0.4时，不考虑涂抹影响（J=0）。

4.9.2.3　塑料排水带地基的沉降计算

塑料排水带（或砂井）地基，虽然打入竖向排水体后，改变了它的排水固结条件和性能，也对土的结构产生了局部扰动，但是对地基土的压缩性及沉降的影响却比较小，所以排水带地基的沉降仍然可以用经典的沉降计算公式计算。考虑到排水带地基土的弹性模量及次固结系数等不易准确测定，建议采用主固结沉降配合经验系数计算排水带地基的沉降，即

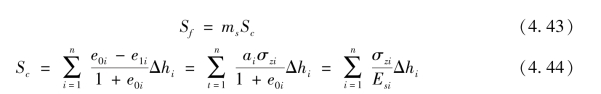
式中：Sf为最终沉降量。

也可以用压缩指数Cc计算主固结沉降量，采用e-logp曲线时，对于正常固结及超固结情况分别见式（4.45）和式（4.46）

正常固结情况：

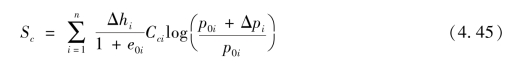
超固结情况：

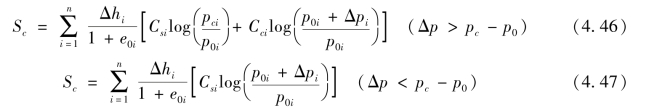
式中：Sc为最终主固结沉降量；ms为经验修正系数，堆载预压，ms=1.1～1.4；真空预压，ms＞1.2；ai，Esi分别为第i层计算点σzi对应的压缩系数和压缩模量；e0i，e1i分别为第i层土计算点的天然孔隙比和pi=p0i+σzi压力下对应的孔隙比；Δhi为分层厚度；σzi为第i层土中点的附加应力；Cci为第i土层的压缩指数；Csi为第i土层的回弹指数。

必须指出，式（4.44）～式（4.47）中的压缩系数a，压缩模量Es和压缩指数Cc，一般都是由常规压缩试验求得的，试验的加载条件都是正压固结压缩，因此，它只能适用于正压条件下的沉降计算，即适用于堆载预压、自重预压等的沉降计算。对于真空预压（即负压和吸力）的条件，经试验证明：负压（吸力）条件下的压缩系数和固结系数比正压的大，因此，计算真空预压条件的沉降时，建议采用负压条件下压缩试验所得的压缩性参数进行计算。沉降经验修正系数ms也是这样，由正压荷载作用下地基沉降求得的修正系数，同样也只能适用于堆载预压情况；在真空预压条件下沉降的经验修正系数，仍然采用常规试验正压条件的压缩系数计算沉降，该经验修正系数ms＞1.2，不是ms＜（0.8～1.0），这是值得注意的。

4.9.2.4　地基强度增长的计算

在设计时，为了预计预压排水固结引起地基承载力与稳定性提高的程度，首先要估算地基强度的增长。根据土力学原理，天然地基在自重作用下固结，本身具有天然强度。在外加荷载的作用下，一方面由于地基排水固结，土中有效应力增大，引起地基土的强度增长；另一方面，地基由于剪切变形或蠕变，又会引起地基强度的衰减。因此，预压排水固结引起地基强度的增长可用式（4.48）来表示

根据有效固结强度理论：对于正常固结饱和软黏土，地基强度增长值Δτc可按式（4.49）计算

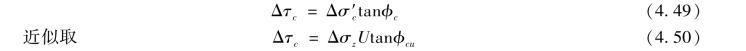
则时间t地基强度的增长值为

式中：τft为荷载作用下，历时t对应的地基强度；τ0为天然地基土的抗剪强度，可采用天然地基土的三轴试验不排水抗剪强度cu，或原位十字板试验强度测定值；Δτc为荷载作用下地基排水固结引起的强度增长值，按式（4.50）计算求得；η为由于剪切蠕动和剪切速率的减慢引起地基强度折减的系数，η=0.90～0.95；σz为计算点的竖向附加应力；Ut为计算点历时t的固结度。