反滤设计中的重要概念

4.1.3.1　等效孔径

等效孔径（equivalent opening size）是土工织物的一个特有的概念。众所周知，不管是织物的透水性抑或保土性，均与织物的孔径大小密切相关，而织物孔径的大小是不等的。为了解织物中不同孔隙孔径的分布情况，可以作出“孔隙分布曲线”（图4.1），它是反滤层设计的重要依据。在设计中需要用到一些特征孔径，如“等效孔径”等。在美国，该等效孔径也称为“表观孔径AOS（apparent opening size）”，以O95表示。关于“等效孔径”的定义，在有些书籍中说得不够确切，容易引起混乱。确切地说，所谓“等效孔径”O95，系指在织物的孔径分布曲线中（图4.1，Atmatzidis D K等2006），对应于95%的那个孔径，也就是说，在织物的大小不同孔隙中，有95%的孔径小于该孔径。这个概念与土的粒径分布曲线十分相似，故很好理解。如果把它定义为所谓“颗粒筛余率”等，则不仅不好理解，而且容易误解。因为“颗粒筛余率”与O95的试验方法有关，而试验方法是可以发展和变化的，故直接将“筛余率”作为定义是不妥的。

确定O95值的方法，中国、美国等均采用间接法中的干筛法（SL/T 233—1999《土工合成材料测试规程》，1999）。在欧洲和加拿大，将等效孔径称为反滤孔径FOS（filtration opening size），其确定方法为湿筛法。一般认为，湿筛法比干筛法要优越，但比较麻烦。据试验，采用干筛法求得的等效孔径比湿筛法略大（可大25%）（王钊，2002），这些方法均属间接法。有条件时也可用直接法，如水银压入法、图像分析法等。应当指出，用不同测试方法求得的孔隙分布曲线，有时可以差别很大（图4.2）。

4.1.3.2　保土性和透水性

反滤设计准则是指反滤设计中应遵循的原则和具体方法。国际有关土工织物反滤准则的研究，始于20世纪70年代。早期的准则大都从太沙基的粒状滤层的反滤准则演变过来的。以后其他欧美国家也相继提出了各自的准则。有人统计（Palmeira，2002），截至1999年底，各种反滤准则不下29种，还可细分为64种。

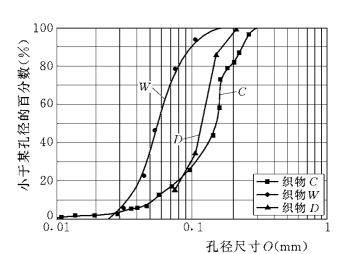
图4.1　典型的孔径分布曲线（无纺织物）（Atmatzidis et al，2006）

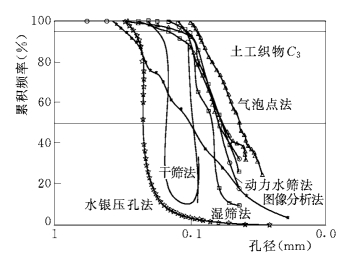
图4.2　织物孔径不同测定方法的结果比较

根据反滤的定义，土工织物反滤层的设置，主要应考虑两方面的问题：保土性与透水性（包括长期透水性）。保土性即要求保证土中起骨架作用的较大的颗粒不流失。保土准则虽然很多，但大多数的保土准则可以用一个式子来表达，即

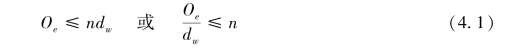
式中：Oe为等效孔径；dw为土的某一特征粒径；n为系数。

对于不同的准则，Oe，dw是不同的，n值也可以相差很大，而且它取决于很多因素。例如，《水利规范》中，Oe采用O95；dw采用d85，而n值则如《水利规范》表4.2.2所示。这样就构成了《水利规范》中的保土准则。其他形式的保土准则将另行叙述。

反滤准则的提出是与织物反滤的工作机理研究密切相关的，同时，准则中各种参数的确定也与特定的测试方法相联系。

至于透水准则[《水利规范》中式（4.2.3-1）]，它表明了反滤织物透水性与土的渗透性的关系。对砂性土，两者应当相等或接近；而对黏性土，则织物的孔径应比土的粒径大得多，因为黏性土颗粒常以团粒的形式存在，而团粒的尺寸远比单一黏土颗粒为大。故织物滤层的孔径尺寸较大。同时土粒在滤层织物的孔口处也容易产生“拱效应”，因此孔口尺寸也应大一些。

4.1.3.3　织物的长期透水性（防淤堵准则）

织物在长期的运用中，其孔眼易被土颗粒堵塞，使透水性减少，因此存在长期透水性的问题。

在初期阶段，透水性比保土性更容易满足。但是随着时间的推延，如果发生了织物淤堵现象，那么透水性就变得更为重要且难以满足，在前面的反滤定义中提到“长期有效性”，就是针对这个难点而提出的，体现在《水利规范》中，即是4.2.4条的防淤堵准则。欲达此目的，织物的孔径应在允许范围内尽可能大些，以防止细颗粒在滤层内积累，或在织物表面形成“土饼”，同时，应使那些已被水流带动的细粒尽可能通过滤层而排出，以防织物的透水性显著降低；但另一方面，又要求滤层的孔径足够地小，防止起骨架作用的颗粒大量流失，引起基土管涌。这就使滤层的设计处于“两难的境地”。但是这个矛盾并不总是同时存在于织物滤层中，在初始阶段，只要基土中较大的骨架颗粒不发生大量的、持续的流失，使基土能维持稳定，那么随着时间的推移，只要织物内不发生严重淤堵，织物的透水性将不致显著地降低（据某些资料，透水性在初期和后期可降低约5倍），故滤层的长期有效性是可以维持的。这样看来，防淤堵准则在反滤设计中就显得十分重要。有关防淤堵问题，在重要和大中型工程中需通过室内的模拟试验，或进行长期观测来检验。

从上述的叙述中，我们可以得到一个认识，即反滤设计的思路与一般的结构设计不同，它没有“偏于安全”的“保守”设计概念，而只有一个“最恰当”的合理设计的问题（陈轮等，2005），在织物反滤机理尚未清晰掌握的情况下，“最恰当”的设计是很不容易进行的。

4.1.3.4　透水率和导水率

土工织物用于反滤层时，表示渗透性的指标是垂直渗透系数kn和透水率ψ，因为这时的水流是垂直于织物平面的；而当土工织物用作排水材料时，表示渗透性的指标是织物的平面渗透系数kp和导水率θ，因为，这时的水流方向是沿着织物平面的。

由于kn和kp与织物的厚度有关，使用起来不便，故常常采用透水率ψ和导水率θ两个指标，它们之间的关系如下。

透水率定义为水头差等于1时的渗透流速，即(www.xing528.com)

而渗透系数是渗流的水力比降等于1时的渗透流速，即

式中：t为织物的厚度；Δh为织物上、下游的水头差；ν为渗透流速；i为水力比降。

故

由此，当测量透水率时，无需测量土工织物的厚度。类似地，织物的平面渗透系数kp定义为水力比降等于1时的渗透流速，即

而导水率定义为沿织物平面的渗透系数kp与织物厚度的乘积，即

若令q为织物平面输导水流的流量则式中：B为试样宽度，cm。

因此，导水率也可定义为比降等于1时，单位宽度织物沿平面排导的水量。上述两个参数的测试方法，可参考有关文献（陆士强等，1994）。

应当指出，透水率与导水率均不是一个常数，它们会随织物上的压力而变。同时，水流状态、水流方向与织物经纬的夹角，水中含气量和水温等也有密切的关系，这点在设计反滤织物和排水织物时应特别注意。

在工程设计中，经常用到的是渗透流量值的计算公式，有了上述的关系，渗透流量的公式可分列如下。

垂直于织物平面的流量qn：

平行于织物平面的流量qp：

式中：Δhgp为沿织物表面上、下游计算点的水头差；Δhgn为土工织物上、下游的水头差；t为织物的厚度；Lg为沿织物表面上、下游计算点的距离；A、B分别为垂直于和平行于土工织物的渗水面积，m2。

在式（4.8）、式（4.9）中避开了随压力而变的厚度参数t，应用比较方便。《水利规范》中的4.3.2条和4.3.3条中的公式，即按此表达。

还应指出，上面讨论的渗透性均对起始状态而言，在织物反滤运用过程中，由于淤堵及其他一些因素影响，使织物透水能力下降。因此，考虑长期效果时，织物渗透性能应乘一个折减系数（将在下面述及）。但另一方面，由于与织物相邻的土体中，有部分细颗粒流失，其渗透性反而会增大。由此启示我们，应当把土工织物和相邻土体构成的整个体系作为一个“反滤系统”来考虑。无疑，对该系统的性能进行理论分析或定量计算是很困难的。实用的方法是将织物与相邻土体在符合工程实际条件下进行试验，以作为设计的依据，而不是简单地仅用织物本身的渗滤试验成果进行设计，这点应特别引起注意。