箝位机构箝位电压U U=U L=3 V,工作频率f=1 Hz,按图6-2所示的时序提供驱动信号。在不同的驱动电压下角位移的计算值和实验值如图6-27所示。从图6-27可以看出,角位移呈阶梯状增长,表明设计的旋转致动器可以实现角位移的累积输出,计算曲线和实验曲线的变化规律基本保持一致。由于箝位机构的动作、外界振动和驱动信号的相互干扰等因素的影响,实验曲线每个阶梯状的顶部不是平直的,而是出现了一定的规律性波动。

图6-27 不同驱动电压下角位移的计算值和实验值(书后附彩插)
不同频率下,旋转致动器输出角位移随驱动电压的变化曲线如图6-28所示,当驱动电压较低时(<2 V),角位移增长较缓慢;当驱动电压达到中等时(2~6 V),输出角位移和驱动电压基本呈线性关系;当驱动电压超过6 V时,曲线的增长趋势逐渐变得平缓。角位移-电压曲线的变化规律符合GMM的性能特性。
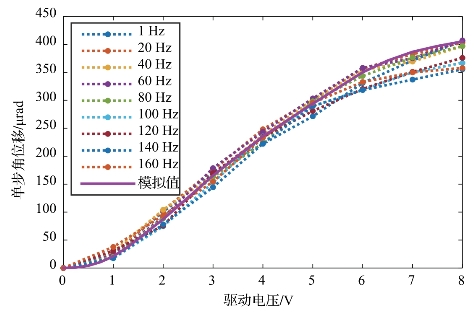
图6-28 不同频率下角位移随驱动电压的变化曲线(书后附彩插)(https://www.xing528.com)
在驱动电压U D<2 V时,磁场强度较低,GMM磁致伸缩的改变主要是易磁化方向的磁畴增大,此时磁致伸缩应变响应很小,致动器输出角位移也较小,外部环境因素对致动器输出的影响相对较大,输出状态不稳定,输出的角位移含有部分外界振动,造成计算值和实验值的误差较大,建立的角位移模型在低压条件下精度比较低。
当驱动电压2 V≤U D≤6 V时,磁化过程主要为中等磁场下的不可逆畴壁运动,磁场强度的改变会使所有磁畴沿易磁化方向产生很大改变,磁致伸缩应变与磁场强度基本呈线性关系。从图6-28可以看出,在此电压范围内,实验值基本呈线性变化,且与计算值基本吻合,计算值与实验值的最大误差和最大相对误差为8.55 μrad和4.52%。建立的角位移模型能较准确地反映致动器的角位移输出。
当驱动电压U D>6 V时,磁场强度达到高磁场,磁化过程主要为磁畴内磁矩的旋转过程,所有磁畴旋转到外磁场方向,磁致伸缩应变响应逐渐变小,达到饱和磁致伸缩状态。另外,由于风扇的散热效果不佳,电压增大引起的线圈温升和涡流损耗也会使磁致伸缩应变减小,故计算值大于实验值,建立的角位移模型也不适用于接近饱和状态的高电压情况。
U U=U L=3 V、U D=5 V的驱动条件下,频率分别为1 Hz、80 Hz和160 Hz时,致动器的角位移的模拟值和实验值曲线如图6-29所示。从图6-29中可以看出,模拟值和实验值基本吻合,随着频率的升高,由于电流的滞后和致动器的阻尼等方面的影响,角位移的滞后现象逐渐变得明显,建立的角位移模型在工作频率范围内能够准确地反映箝位式旋转致动器的角位移输出。
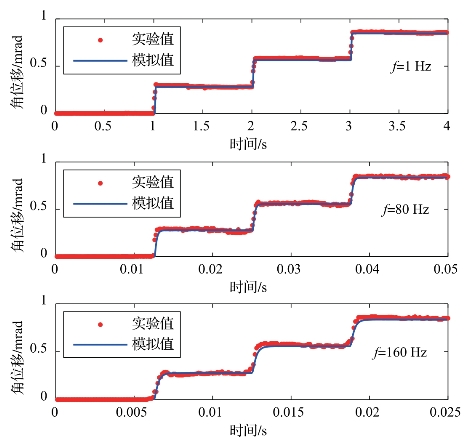
图6-29 不同频率下的角位移模拟值和实验值(书后附彩插)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




