柔性铰链驱动的设计优化

柔性铰链作为致动器的弹性元件，既为GMM棒提供预压力，又为驱动机构复位提供回弹力，GMM棒输出时还要克服柔性铰链的弹性，其性能直接影响致动器的输出。旋转致动器的箝位机构和驱动机构都采用直角柔性铰链作为弹性元件，如图6－6所示。柔性铰链最重要的设计指标就是刚度，柔性铰链的刚度大小要适中，不能过大或过小。刚度过大，一是GMM棒伸长时会消耗过多的能量，降低致动器的输出能力；二是GMM棒伸长过程中会引起压应力产生较大的变化，影响致动器的线性输出，一般弹性元件的刚度不超过GMM棒刚度（k G＝1.5×107 N／m）的25%［83］。刚度过小，预压装置必须输出更大的位移才能提供所需的预压力，这会增大致动器的尺寸。除柔性铰链的刚度要满足设计要求外，还应兼顾应力集中和安装空间等因素。另外，柔性铰链刚度的准确计算是致动器精确建模的必要前提。

柔性铰链作为致动器的弹性元件，材料选用弹性性能较好的65Mn弹簧钢。为便于柔性铰链的受力分析计算，对柔性铰链做出如下假设：

（1）柔性铰链材料为均匀各向同性材料。

（2）三个驱动柔性铰链严格沿圆周均布，三者受力完全相同；三个箝位柔性铰链严格沿圆周均布，三者受力完全相同，单个箝位柔性铰链两侧严格对称。

图6-6　箝位柔性铰链和驱动柔性铰链

1．结构设计

驱动柔性铰链的受力和工作原理如图6－7所示。驱动柔性铰链、定子和底座制成一体，底座固定不动，三个驱动柔性铰链在沿圆周上均匀分布，将底座和定子柔性连接在一起。三个驱动机构圆周上均匀分布，驱动机构上电时，三个驱动机构同时输出驱动力F作用在定子上，相当于定子在转矩M的作用下绕轴心O转动角位移θ，此时驱动柔性铰链产生弯曲形变。

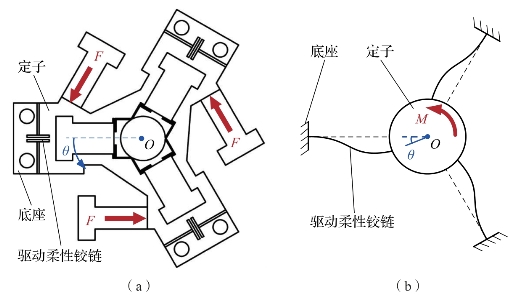
图6-7　驱动柔性铰链的受力和工作原理

（a）受力分析；（b）工作原理

驱动柔性铰链受力产生弯曲形变时，由于受到拉应力的影响，刚度是不断变化的，其载荷－位移特性曲线是非线性的，形变越大时，其非线性特性越明显，尤其是位移超过柔性铰链长度的10%时，载荷－位移的非线性便会变得非常明显［139］。通过有限元法对驱动柔性铰链进行载荷－位移变化规律的仿真模拟分析，得驱动柔性铰链（尺寸为10 mm×10 mm×1 mm）的载荷－位移曲线，如图6－8所示。从图6－8可以看出，当位移较小时，载荷－位移曲线基本呈线性变化；当位移达到0.2 mm（柔性铰链长度的2%）时，载荷－位移的非线性开始变得明显。GMM棒的磁致伸缩系数非常小（1.0×10－3），经计算，GMM棒输出达到最大时，驱动柔性铰链的位移约为24 μm，仅为长度的0.24%，远远小于2%。所以，可以忽略拉应力对刚度的影响，驱动柔性铰链都是线性弹性变形，即将柔性铰链的刚度看成是恒定的。同理，后文中箝位柔性铰链和叠加式柔性铰链的刚度也看成是恒定的。

图6-8　驱动柔性铰链的载荷-位移非线性曲线

将单个驱动柔性铰链简化为超静定梁，其受力分析如图6－9所示，OA段为驱动柔性铰链，截面惯性矩为I，AB段为定子，假设为刚性。

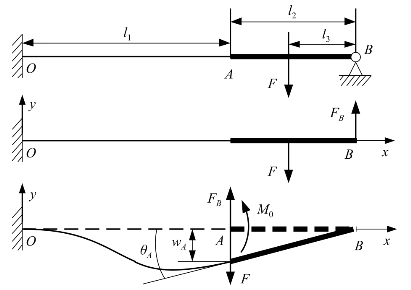
图6-9　驱动柔性铰链受力分析

解除B点约束，假设B点受到的支反力为FB，将力F和FB平移到A点，M 0为F和FB对A点产生的转矩，M 0＝FB l2－F（l2＋l3）。柔性铰链OA段上任一点x的弯矩为

任一点x的转角θ和挠度w为

式中，E为柔性铰链的弹性模量；I为柔性铰链的截面惯性矩（I＝ab3／12，a为柔性铰链宽度，b为柔性铰链厚度）；C1、C2为常数。

由θ（0）＝0，w（0）＝0，得C1＝C2＝0。点A的转角和挠度分别为(www.xing528.com)

由于θA非常小（最大为1.11 mrad），故点B的挠度可近似计算为

将式（6－4）、式（6－5）代入式（6－6）得

将式（6－7）代入式（6－4）得点A的转角：

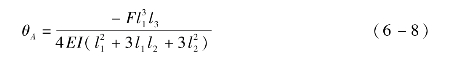
驱动柔性铰链在力F作用下绕轴心的等效转动刚度k D为

式中，l1、a和b分别为驱动柔性铰链的长度、宽度和厚度，宽度a与线圈的外径一致，取a＝10 mm。驱动柔性铰链的等效转动刚度随长度、厚度的变化曲线如图6－10所示。驱动柔性铰链的等效转动刚度k D与厚度b成正比，与长度l1成反比。驱动柔性铰链厚度和长度的取值要合适，长度l1越大，致动器的整体尺寸就会越大；厚度b越小，强度就越低，而且加工误差对刚度的影响就越大，加工难度也越大。综合考虑空间、加工和强度等因素，确定驱动柔性铰链的长度l1＝10 mm、厚度b＝1 mm。由式（6－9）计算得驱动柔性铰链的等效转动刚度k D＝9.90×104 N／rad，是GMM棒等效转动刚度（l3 k G）的18.3%，符合设计要求。在预应力为10 MPa条件下，GMM棒达到最大磁致伸缩时，GMM棒的压应力增大至12.3 MPa，此时磁致伸缩系数变化不大（见图2－11），工作中压应力的变化对GMM棒的线性输出影响较小。最终确定驱动柔性铰链的尺寸为10 mm×10 mm×1 mm。

图6-10　驱动柔性铰链的等效转动刚度随长度、厚度的变化曲线

2.有限元分析验证

在有限元分析软件COMSOL中进行强度校核，驱动GMM棒输出最大位移时，驱动柔性铰链的应力分布如图6－11所示（为便于显示，图中局部放大图去掉了驱动柔性铰链两侧刚性部分）。从图6－11可以看出，应力主要集中在驱动柔性铰链两端根部，驱动柔性铰链外、内两端的最大应力分别为84.39 MPa和90.58 MPa，内端稍大于外端，均小于65Mn弹簧钢的极限强度785 MPa。

利用有限元分析软件COMSOL对驱动柔性铰链的等效刚度计算结果进行验证，图6－12所示为驱动力F＝20 N时，驱动柔性铰链的挠度曲线。从图6－12可以看出，由式（6－3）得出的计算值和有限元模拟值基本一致；随着柔性铰链长度的增加，挠度逐渐减小，减小趋势先快后慢，其变化规律与图6－9中的分析一致，表明了上述计算方法能够准确描述柔性铰链挠度的变化规律。

图6-11　驱动柔性铰链的应力分布图

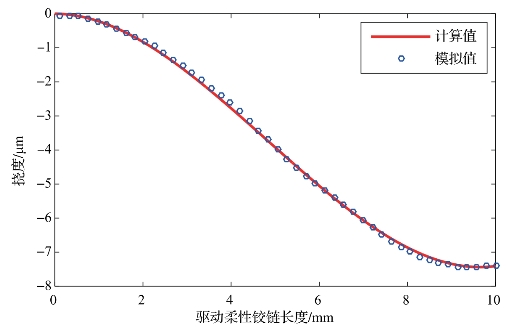
图6-12　驱动柔性铰链的挠度曲线

图6－13所示为驱动柔性铰链的力－角位移曲线。从图6－13中可以看出，由式（6－9）求得的计算值和有限元模拟值基本吻合，模拟值曲线基本呈线性变化（即刚度是恒定的），这是由于在GMM棒的输出位移范围内，柔性铰链的形变较小，拉应力对刚度的影响较小，力－角位移曲线基本呈直线，同时也验证了将驱动柔性铰链的刚度看成恒定是成立的。驱动柔性铰链等效转动刚度的计算值和模拟值分别为9.90×104 N／rad和9.73×104 N／rad，相对误差为1.78%，证明了驱动柔性铰链等效转动刚度计算方法的正确性。

图6-13　驱动柔性铰链的力-角位移曲线