将叠加式柔性铰链简化成“质量-弹簧-阻尼”单元,GMM棒伸长时,推动两个质量块反向运动,伸长过程可等效为双自由度动力学模型,如图4-17所示。图4-17中m1、m2、y1、y2、f1和f2分别为质量块A和质量块B的质量、位移和受到的摩擦力,k F和c F分别为柔性铰链的等效刚度和等效阻尼,m G1和m G2分别为GMM棒向左和向右移动部分的等效质量,m F1和m F2分别为柔性铰链向左和向右移动部分的等效质量,F G为GMM棒的输出力。质量块A、GMM棒左端和柔性铰链左端刚性相连,三者具有相同的位移、速度和加速度;质量块B、GMM棒右端和柔性铰链右端刚性相连,三者具有相同的位移、速度和加速度,设M 1=m1+m G1+m F1,M 2=m2+m G2+m F2。
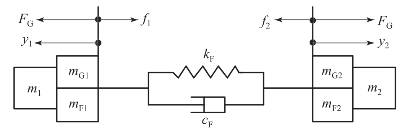
图4-17 伸长过程的双自由度动力学模型
GMM棒伸长时,M2对M1的冲击力F1为
![]()
M1和M 2的大小决定了两个质量块的运动形式,GMM棒伸长时,共有四种运动形式:
(1)M 1=M 2。此时f1=f2,两个质量块受到的冲击力和摩擦力相同,二者反向运动,y1=y2。
(2)M 1>M 2且f1<F1。质量块A受到的摩擦力大于质量块B受到的摩擦力,二者在GMM棒驱动力作用下反向运动,y1<y2。
(3)M1>M2且f1>F1>f2。此时质量块A受到的冲击力不足以克服摩擦力f1,质量块A保持静止,GMM棒推动质量块B向右运动。
(4)M1>M2且f1>f2>F1。此时两个质量块的质量都比较大,GMM棒驱动力不足以推动两个质量块运动,此种情况不予考虑。(https://www.xing528.com)
根据惯性式致动器的工作原理,GMM棒伸长时,需满足第二种运动形式,分别对两个质量块建立动态运动微分方程为
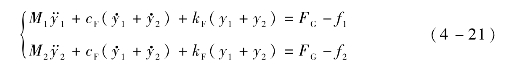
将式(4-21)联立第3章的各物理场模型,可得惯性式致动器伸长状态的位移输出模型,式(4-21)与3.7节中GMM棒多自由度位移模型的对应关系为

为了便于计算机运算,将式(4-21)转化为状态空间表达式。设状态空间向量![]() ,设x1=y1、x2=y2、
,设x1=y1、x2=y2、![]() ,二阶微分方程组可转化为一阶微分方程组:
,二阶微分方程组可转化为一阶微分方程组:
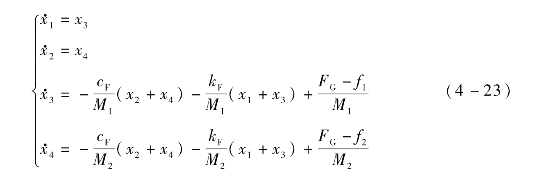
化简为

式中,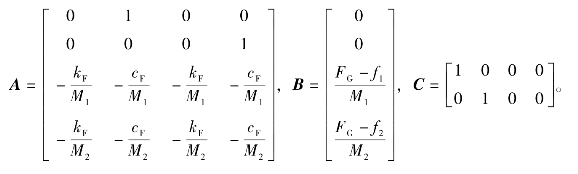
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




