GMM棒位移模型的研究分析

GMM棒轴向磁场强度分布是不均匀的，为了更加准确地描述GMM棒的输出特性，将整个GMM棒离散成多个GMM棒单元，每个GMM棒单元可根据所处的磁场强度单独进行分析，能够充分考虑到磁场强度的不均匀性，可以提高模型的计算精度。每个GMM棒单元等效成“质量－弹簧－阻尼”单元，整个GMM棒由n个“质量－弹簧－阻尼”单元串联而成，如图3－15所示。

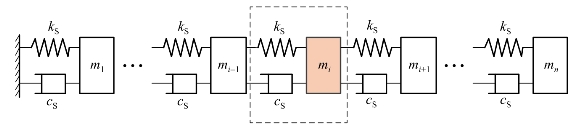
图3-15　GMM棒离散成多个单元

单个GMM棒单元的等效质量计算方法如图3－16所示，图中O点为GMM棒的固定端，A点为GMM棒的输出端。

图3-16　GMM棒等效质量的计算

以能量守恒和质量元的思路来确定GMM棒第i个质量元的等效质量：

式中，mi为第i个质量元的等效质量；v为GMM棒输出端速度；l为GMM棒长度；ρG为GMM棒密度；A G为GMM棒横截面积；x为质量元到坐标原点的距离；d x为质量元轴向长度。

求解得

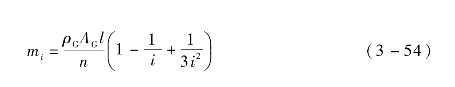
单个“质量－弹簧－阻尼”单元的弹簧刚度k S和阻尼器阻尼c S分别为

式中，E G为GMM棒弹性模量；C G为GMM棒阻尼系数。(www.xing528.com)

单个GMM棒单元在激励磁场作用下伸长，其作用力fi施加在相邻的两个GMM棒单元上，大小相等，方向相反，如图3－17所示，图中F L为负载对GMM棒的反作用力。

图3-17　单个GMM棒单元的受力分析

激励磁场作用在GMM棒单元上的作用力fi为

式中，λ（U，x）为线圈电压为U在轴线上点x处的磁致应变。

各GMM棒单元受到的等效驱动力为

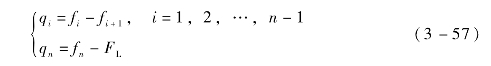
根据振动理论，可得GMM棒单元的运动微分方程：

式中，M、C和K分别为GMM棒单元的等效质量矩阵、阻尼矩阵和等效刚度矩阵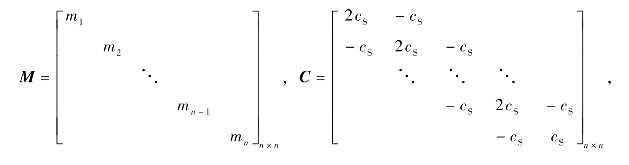，单元位移向量X＝（x1 ，x2，…，xi，…，xn）T，xi为第i个单元的位移；单元输出驱动力向量Q＝（q1，q2，…，qi，…，qn）T，qi为第i个单元上作用的等效驱动力。

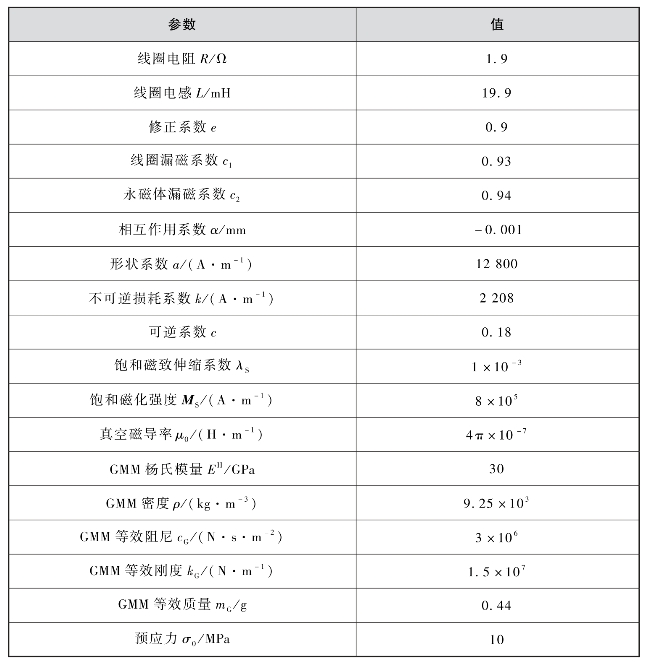
本章模型中相关的参数设置见表3－2。

表3-2　建立模型的参数设置