静态磁化模型优化方案

GMM属于铁磁性功能材料，存在本征磁滞非线性，即GMM的磁化强度M总是滞后于磁场强度H的变化，磁化强度的磁滞是整个致动器迟滞现象的主要组成部分，如何准确地描述这种磁滞非线性关系，是致动器精确建模的重要环节。

根据Weiss分子场理论，施加一个较大范围的磁场，才能使GMM从开始初始磁化达到完全饱和磁化，在此磁场范围内，施加的外部磁场改变磁畴自发磁化形成的磁矩方向，而磁畴之间也存在着相互作用的内部磁场，内部磁场使磁畴转到磁矩相互平行的方向。另外，对GMM施加预压力产生的应力也会产生影响磁畴运动的磁场，从而影响GMM棒的磁化强度。

根据微磁学理论，由于磁畴的大小、形状、磁矩方向和磁畴间销连接点等结构的不同，以及磁畴所受到的应力不同，导致GMM在磁化过程中磁畴畴壁的移动和磁畴的转动并不是完全可逆的，这些不可逆的磁畴运动导致了系统能量的损耗，故产生了磁滞现象。

在Weiss分子场理论和微磁学理论的基础上，Jiles和Atherton提出了著名的J－A磁化理论模型［99，103］，此模型建立了外加磁场和磁化强度的关系式：

(www.xing528.com)

式中，H e为GMM材料的有效磁场；H为外加磁场（H＝H C＋H B，H C为线圈产生的驱动磁场，H B为永磁体产生的偏置磁场）；αM为GMM材料磁畴间相互作用产生的磁场（α为磁畴畴壁间相互作用系数，M为磁化强度）；Hσ为预应力σ0作用下产生影响磁畴运动的磁场；中间参数（λS为饱和磁致伸缩应变，μ0为真空磁导率）；M an为磁畴转动时产生的完全可逆的无磁滞磁化强度；M S为饱和磁化强度；a为无磁滞磁化强度形状系数；M irr和M rev分别为磁畴畴壁移动产生的不可逆磁化强度和畴壁转动产生的不可逆磁化强度；δ为符号常数（当H增加时，δ≡1；当H减少时，δ≡－1）；k为不可逆损耗系数；c为可逆系数。

通过J－A模型得到的磁化强度随磁场强度的变化规律曲线如图3－13所示，从图中可以看出，磁场强度由0增加到最大值时，磁化强度基本呈线性增加；磁场强度由最大值逐渐减小时，磁化强度保持一段的缓慢减小，然后才线性减小至最小值；由最小值逐渐增大时，磁化强度同样滞后一段时间，保持一段的缓慢增大，然后才逐渐线性增大到最大值，由此不断重复。

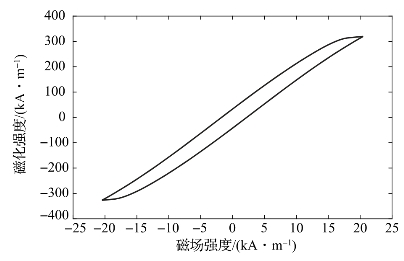
图3-13　J-A模型得到的磁化曲线