基于毕奥-萨伐尔定律的磁场模型优化方案

毕奥－萨伐尔定律经常用于计算均匀密绕直螺线管的磁感应强度，其计算方法如图3－8所示。线圈由等直径的漆包线缠绕而成，以直螺线管轴线中点为坐标原点O，直螺线管长度为2 l0，内径为R1，外径为R2，单层线圈匝数为N1，线圈缠绕层数为N2，通电电流为I。

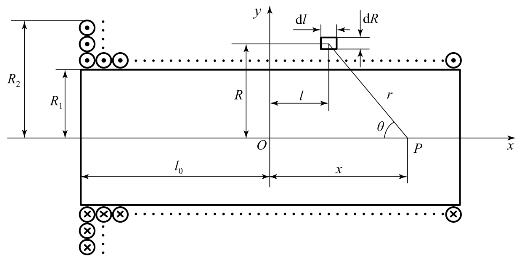
图3-8　密绕直螺线管磁场强度计算示意图

选择线圈上半径为R、轴向坐标为l的一小块区域d l d R作为研究对象，其轴向长度为d l，径向长度为d R，则该小块区域的电流可表示为

P点为空心圆柱线圈轴线上的任一点，其坐标为x，到研究的小块区域中心距离为r，，根据毕奥－萨伐尔定律，区域d l d R圆环激励电流在P点产生的轴向磁场强度d H为

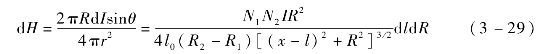
对圆环激励电流产生的磁场强度d H进行积分，可得整个圆柱线圈在P点产生的磁场强度：

先对单层线圈进行积分，即对d l进行积分，通过变换将d l积分转换为对dθ的积分，如图3－9所示。

图3-9　对单层线圈的积分

由三角函数得

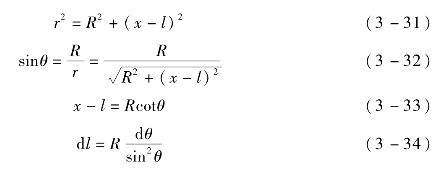
将式（3－34）代入式（3－29）得

式中，。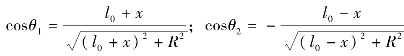

再对线圈厚度进行积分，即对d R进行积分，通过积分变换将d R积分转换为对dα和对dβ的积分，如图3－10所示。(www.xing528.com)

由三角函数得

图3-10　对线圈厚度的积分

将式（3－38）代入式（3－36）得

式中，。

通过毕奥－萨伐尔定律计算的磁场强度是在线圈内部为真空、无漏磁的理想条件下得到的。但在实际中，线圈中为GMM棒材料，GMM棒和线圈之间还有空气间隙，GMM棒两端和轭铁间也有空气间隙，这些现实条件在一定程度上都会产生漏磁现象，因此，需要对通过毕奥－萨伐尔定律计算的线圈磁场强度进行修正，可通过线圈漏磁系数C1对磁场强度进行修正。

线圈芯和致动器各零部件的材料对GMM磁场的均匀性有很大影响，线圈单独处在真空环境中，此时线圈磁场强度的均匀性最差；线圈芯为高导磁材料且形成磁回路时，如果忽略漏磁的影响，此时线圈内部磁场可看成均匀的；另外，致动器驱动机构各部分材料的磁导率对线圈磁场的均匀度也有一定的影响。

线圈内部GMM棒的磁导率比较大，GMM两端的轭铁采用的是高导磁材料，而高导磁材料具有聚合磁力线的作用，其会在一定程度上提高磁场的均匀性，即在一定程度上提高磁场强度，但不应超过磁场轴线中心处的磁场强度。高导磁材料对磁力线的聚合作用与距离x成反比，设其影响系数为C2：

式中，m、k为常数；l0为线圈长度的1／2。

则经过两次修正后，激励线圈轴向磁场强度H（x）为

基于磁路建立的磁场模型方法简单，但精度较低；基于毕奥－萨伐尔定律建立的磁场模型计算方法复杂，但更加准确。如图3－11所示，当电流分别为1 A、2 A和3 A时，通过上述两种计算方法得到的线圈轴线上磁场强度的分布（图中实线为毕奥－萨伐尔磁场模型，虚线为基于磁路的磁场模型）。从图3－11可以看出，基于磁路建立的模型为一条直线，得到的是线圈轴线上的平均磁场强度；基于毕奥－萨伐尔定律建立的磁场模型磁场强度并不是均匀分布的，呈中间强、两端弱的分布，磁场强度在线圈两端的变化比较大，基于毕奥－萨伐尔定律建立的磁场模型，能够更加准确地反映线圈轴线上磁场强度的分布情况。但当计算精度要求不高或者GMM棒的长度小于线圈长度到一定程度时，即GMM棒处于线圈磁场强度较均匀区域时，也可用磁路建立的磁场模型来计算磁场强度。

图3-11　两种计算方法得到的磁场强度分布