线圈简化为RRL电路

将线圈简化为RL电路形式简单，计算简便，尤其适用于频率较低的单匝线圈。但对于高频率的多匝线圈，频率越高，线圈的趋肤效应变得越明显，导致线圈的有效截面积逐渐减小，电阻增大，其功率损耗也相应增大。为了更加准确地描述电流的响应，可在RL电路的基础上引入并联电阻R′。同样采用叠加方式对电路的电流响应进行计算，对电路施加阶跃信号时，其等效电路图如图3－5所示。

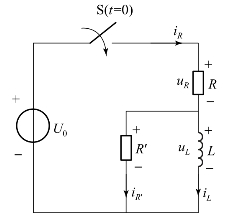
图3-5　线圈简化成RRL电路图

针对正方波中的U0 U（t）阶跃信号，当T≥0时，由基尔霍夫电压定律（KVL）得

由于iR1＝iL1＋iR′1［iR1、iL1和iR′1分别为U0 U（t）阶跃信号时R、L和R′的电流］，，可得电感电流iL1的微分方程：

电感电流iL1的通解为

式中，A为待定常数。

将初始条件iL1（0＋）＋iL1（0－）＝0代入得

(www.xing528.com)

用同样的求解方法得正方波信号的电感电流iL响应为

同理，对于锯齿波信号可得激励线圈的电感电流iL响应为

分别在1 Hz、10 Hz、125 Hz和250 Hz条件下，测试驱动线圈的电流响应，使用MATLAB软件中的参数辨识方法确定RL电路和RRL电路的参数值，参数辨识结果和两种方案平均误差见表3－1。

表3-1　参数辨识结果和两种方案平均误差

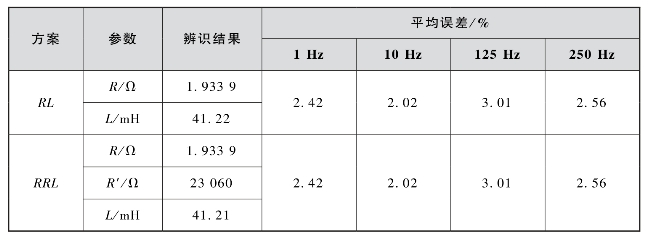
从辨识结果和平均误差结果来看，两个方案的平均误差基本相同。由于致动器的最大工作频率只有210 Hz，线圈的趋肤效应不明显，在250 Hz时，方案二的平均误差只比方案一小1.3×10－3%，但方案一形式更简单，计算更方便，所以选择式（3－18）和式（3－19）分别作为正方波信号和锯齿波信号的电流解析式。图3－6所示为不同频率下正方波信号电流响应的计算值和实验值曲线。从图3－6可以看出，频率越高，电流的延迟现象越明显，在工作频率范围内（后续设计的致动器的工作频率均低于250 Hz），计算值和实验值基本吻合，电流解析式能准确地反映电流的响应特性。

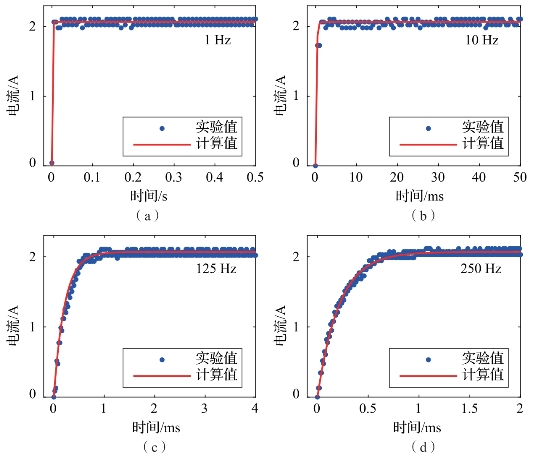
图3-6　不同频率下正方波信号电流响应的计算值和实验值曲线（书后附彩插）

（a）1 Hz；（b）10 Hz；（c）125 Hz；（d）250 Hz