【摘要】:为了验证模型计算结果的合理性,该算例计算结果与HECRAS 4.1计算结果相比较,比较结果详见图3.12~图3.14。图3.12计算河段3第一个断面水位过程和流量过程从图3.12~图3.14可以看出,即使较为复杂的河网,该程序运行仍较为稳定;计算的结果在精度上与HECRAS 4.0计算结果较为吻合,说明程序的计算精度可以接受。图3.13水库1水位过程和流量过程图3.14计算河段8过桥后断面水位过程和流量过程
图3.10所示为Hec-ras自带菱形河网系统算例,也可将其作为验证实例,用以验证模型对复杂河网系统的适应性和计算精度。
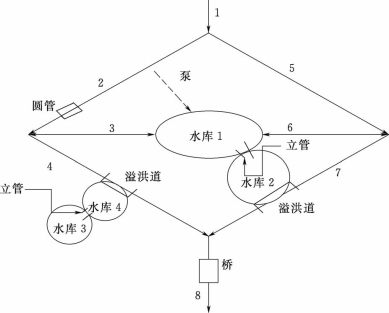
图3.10 菱形河网模型
1.计算参数
该河网的河道断面为典型的规则梯形复合断面(图3.11),河道平均坡度为0.000095,Manning系数主槽为0.03,河滩为0.05。计算河段1上游给定一个流量过程,计算水利段8下游边界条件由Manning公式来确定设置为平均坡度0.000095,时间步长为15min。其他参数参考hecras4.1exampleproject/unsteadyexamples中的设置。
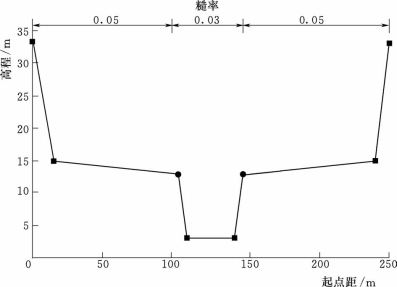
图3.11 河道断面形状示意图
2.计算结果比较(https://www.xing528.com)
根据应用上述河网计算参数和项目所构建的一维河网水动力计算模型,对菱形河网系统进行水力计算。为了验证模型计算结果的合理性,该算例计算结果与HECRAS 4.1计算结果相比较,比较结果详见图3.12~图3.14。
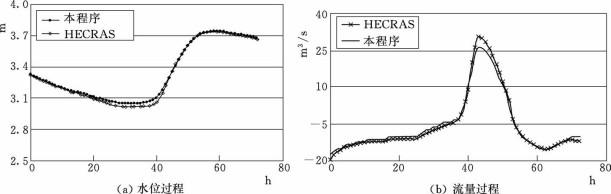
图3.12 计算河段3第一个断面水位过程和流量过程
从图3.12~图3.14可以看出,即使较为复杂的河网,该程序运行仍较为稳定;计算的结果在精度上与HECRAS 4.0计算结果较为吻合,说明程序的计算精度可以接受。其计算结果的差异可以理解为不同计算模型对各种水利工程的控制运行计算方法的差异。
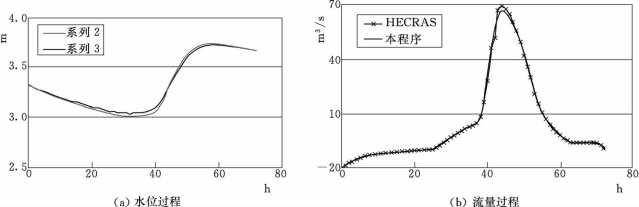
图3.13 水库1水位过程和流量过程
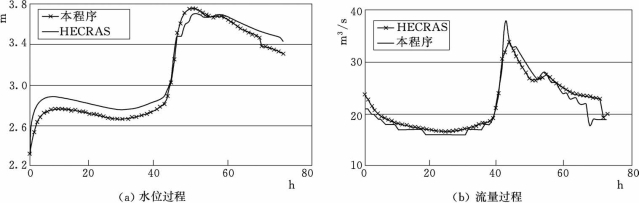
图3.14 计算河段8过桥后断面水位过程和流量过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




