河流水动力学控制方程及求解方法

在数学上，河网水动力过程一般应用Saint-Venant方程组描述，根据问题研究的需要，该方程组有多种表达形式，但本质上是一致的。如果加上旁侧入流，Saint Venant方程组也可采用以断面过流面积A、流量Q为自变量的基本方程组，即

式中 Q——流量；

Z——水位；

A——过流断面面积；

ql——旁侧入流流量；

n——河床Manning系数；

R——水力半径；

G——重力加速度。

平原河网汊点需满足连续性条件和能量守恒条件(或动量守恒条件)，即

方程组式(3.26)～式(3.29)的求解方法有很多，本次研究应用隐格式积分离散方程组式(3.26)～式(3.29)。

在计算区域的任意微元网格内(图3.8)，对式(3.26)和式(3.27)进行积分，有

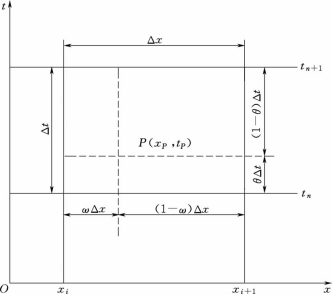
图3.8　Preissmann格式离散积分示意图(www.xing528.com)

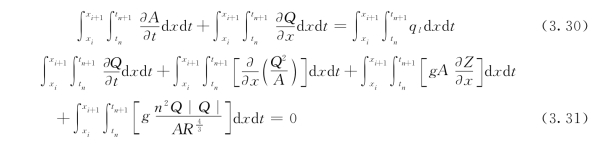
在图3.8中的任意矩形积分微元内，设各参数函数f为线性分布，则在微元内可满足下列等式成立，即

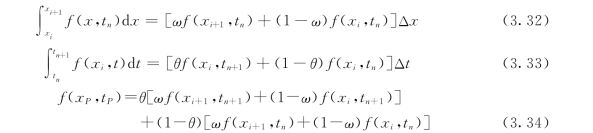
式中 θ——时间加权系数；

ω——空间加权系数；

P——积分微元内的任意点。

式(3.32)和式(3.33)各变量在tn+1时刻均为未知，且对流项为非线性项，因此，需对变量Taylor展开后迭代求解，以任意变量函数G=G(Z，Q)为例，Taylor展开后保留一阶项，即

应用式(3.33)对式(3.26)和式(3.27)进行Taylor展开，合并后可得到

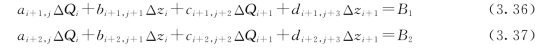
其中ai+1，j、ai+2，j、bi+1，j+1、bi+2，j+1、ci+1，j+2、ci+2，j+2、d i+1，j+3、d i+2，j+3、B 1和B 2均为积分离散和Taylor展开式后各未知变量的系数组合，具体的推导过程和参数表达式可参考相关文献，式(3.36)和式(3.37)为常系数线性方程组。

同理，式(3.28)和式(3.29)可以积分离散为

式中，M和N为式(3.28)和式(3.29)积分离散后，式(3.38)和式(3.39)左边项的余量；河网内如闸坝堰及蓄滞洪区等水利工程设置，根据各自的流量计算公式，应用上述积分离散方法，形成与式(3.36)和式(3.37)类似的离散计算格式，具体的求解过程可参考相关文献。