形心轴的计算方法与应用

计算型钢惯性矩必然涉及形心轴。所谓形心轴，即受力杆件在外力作用下发生弯曲时，上部发生纵向线段收缩，下部发生纵向线段延长，处于中间部位的一段既不收缩也不延长的纵向线段，称之为形心轴或中性轴。见图2-30。

一般承受风压方向Y轴呈对称形状的型钢受力截面形心轴，即为其受力截面（与风压方向垂直）中轴线，其至杆件截面临界边缘线距离，即为形心轴度量值；竖向非对称形状杆件受力截面形心轴，需要将杆件截面分解为几个矩形截面，再分别计算各个矩形截面面积与中轴线至型钢截面临界边缘线距离。然后再按公式计算出型钢形心轴与临界边沿线距离。

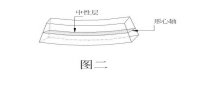
图2-30　形心轴

所谓临界边沿线，即受力杆件在一定风压（外力）的作用下，迎风面（受力）承受收缩挤压应力，与迎风面平行非迎风面（非受力面）承受拉伸弯曲应力。由于杆件所受到拉伸弯曲力破坏远远大于收缩挤压力破坏，故受拉伸弯曲应力的截面边沿线亦为临界边沿线。在计算型钢形心轴时亦以此边沿线为计算基准。

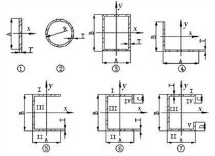
图2-31　几种常见的型钢截面图

由于图2-31中①、②、③、⑤、⑦中型钢为竖向对称形状的受力截面，其形心轴即为竖向截面中轴线，无需进行计算。图2-31④、⑥中型钢均为竖向非对称形状受力截面，需要进行如下计算：

图2-31中④L式型钢形心轴计算：

图2-31中④L式型钢截面可分解为A1、A2两个矩形截面，

其截面面积：A1=（B-T）T；A2=AT

设两个矩形截面中轴线至型钢竖向临界边沿线的距离分别为Y1，Y2，(www.xing528.com)

其中Y1＝（B-T）/2+T；Y2=T/2

设型钢形心轴与竖向临界边沿线的距离YC，

YC＝（A1×Y1+A2×Y2）/（A1+A2）

图2-31中⑥G形型钢形心轴计算：

图2-31中⑥G形型钢截面可分解为A1、A2、A3、A4四个矩形截面，

其截面面积：A1=AT；A2=AT；A3=（B-2T）T；A4=（C-T）

设四个矩形截面中轴线至型钢竖向临界边沿线的距离分别为Y1、Y2、Y3、Y4，

其中Y1=T/2+B-T；Y2=T/2；Y3=（B-2T）/2+T、Y4=（C-T）/2+B-C

设型钢形心轴与临界边沿线的距离为YC，

YC=（A1×Y1+A2×Y2+A3×Y3+A4×Y4）/（A1+A2+A3+A4）

由以上计算可知：型钢某个矩形截面中轴线即矩形截面中心线。型钢截面形心轴是以不同矩形截面面积与其中轴线到型钢竖向截面临界边沿线的叠加、复合、均分而得到的形心轴，也可称之为型钢截面面积中心线。应该特别指出：型钢截面面积与型钢截面是有区别的，所谓型钢截面是指型钢轮廓面积，反映型钢截面大小；所谓型钢截面面积是指型钢持物料（实心）面积，反映钢材具体分布状况，即钢材量多少。对于异型截面形状型钢、异型材等材料，这种划分意义是显而易见的。