控制系统分析实例：根轨迹法和延时环节分析

【例8-1】 使用本章所学的MATLAB命令，对下面的系统进行分析。系统传递函数如下：

其结构图见图8-1。

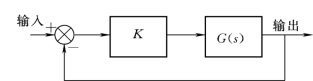
图8-1　系统结构图

频率响应分析：首先可以写出系统的开环传递函数，得到对应K＝1.5 时的系统频率特性波德图。使用logSpace 命令生成具有100 个频率点的对数坐标轴。

＞＞K＝1.5；ng＝1；dg＝poly（[0－1－2]）；

＞＞w＝logSpace（－1，1，100）′；

＞＞[m，p]＝bode（k*ng，dg，w）；

＞＞Subplot（211）；Semilogx（w，20*log10（m））；

＞＞Subplot（212）；Semilogx（w，p）

由其绘制的波德图（见图8-2）可见，系统的幅值裕量与相角裕量大约为10dB 与45°，也可以使用margin命令验证这一点。

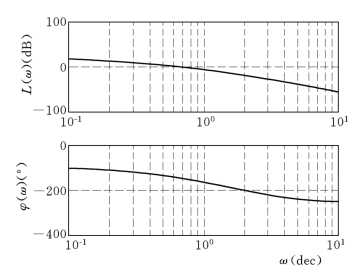
图8-2　系统KG（s）的波德图

＞＞[gm，pm，wpc，wgc]＝margin（m，p，ω）

gm值表示系统增益再增加gm（＝4），系统就由稳定开始转入不稳定。这个值折合为12dB。

下面介绍我们如何求得带有单位圆的极坐标图。为生成一个单位圆，使用linSpace命令建立了一个0～2π的空间向量。这个单位圆是通过在复平面上绘制ejω的虚部与实部的轨迹而得到的。

＞＞w2＝linSpace（0.2*pi，100）′；ejw＝exp（j*w2）；

＞＞r2＝real（ejw）；i2＝imag（ejw）；

＞＞[r，i]＝nyquiSt（k*ng，dg，w）；

＞＞axiS（`Square`）；plot（r2，i2）；axiS

下面一行命令可绘制带有单位圆的极坐标图。

＞＞plot（r2，i2，r，i）；grid；

因为极坐标图中的轨迹没有包围（－1，j0）点，所以图8-3所示的系统是稳定的。注意在图8-4中的幅值裕量为12dB。

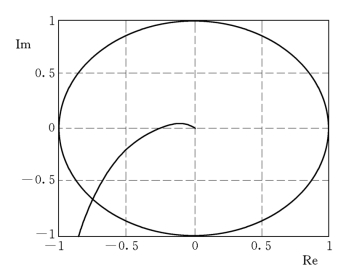
图8-3　例8-1 系统的极坐标图

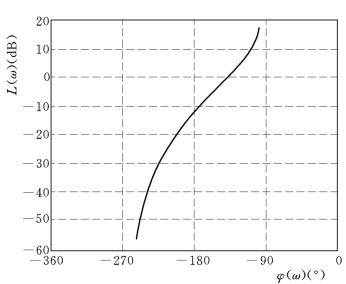
图8-4　KG（s）的尼柯尔斯图

＞＞nicholS（k*ng，dg，w）或plot（p，20*log10（m））

从闭环系统的波德图中，可以得到系统带宽及谐振峰值等特征参数。设T（s）为系统闭环传递函数，使用cloop 命令可求得系统的闭环传递函数：

＞＞[nt，dt]＝cloop（k*ng，dg）；

＞＞mc＝bode（nt，dt，w）；Subplot（211），

＞＞Semilogx[w，20*log10（mc）]；grid

由图8-5可以看到闭环系统谐振峰值是3dB，而带宽约为1rad/S。

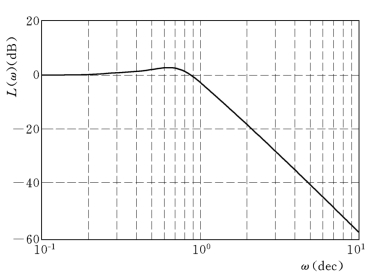
图8-5　闭环系统的对数幅频特性图

根轨迹分析法：下面将使用根轨迹法对于不同的增益的变化预指系统响应。

输入：

＞＞rlocuS（k*ng，dg）

可以得到系统根轨迹图（见图8-6）。

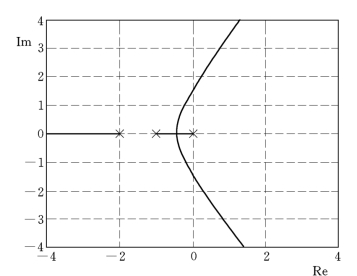
图8-6　系统根轨迹图

使用rlocfind命令，就可以知道当K＞6时，系统变成不稳定系统。还可以通过求得该临界点（K＝6）附近一定范围内极点的参数得到其准确值。

上述数据显示了该区域内增益及对应的闭环极点位置。由此可得出如下结论：

（1）0＜K＜0.4 时，闭环系统具有不同的实数极点，表明系统处于过阻尼状态。(www.xing528.com)

（2）K＝0.4 时，对应为分离点，系统处于临界阻尼状态。

（3）0.6＜K＜6 时，系统主导极点为共轭复数极点，系统为欠阻尼状态。

（4）K＝6 时，系统有一对虚根，系统处于临界稳定状态。

（5）K＞6 时，系统出现右根，系统处于不稳定状态。

为了验证上述结论，我们将求得闭环系统的传递函数，并求得五个系统的阶跃响应，K 值分别为0.25、0.4、1.5、6 和8。MTALAB程序8-1 为求得5 个系统的阶跃响应程序清单。

这五种系统的的阶跃响应（三个是稳定的，两个是不稳定的）见图8-7。

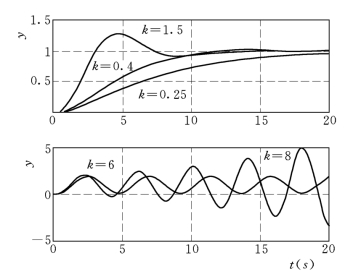
图8-7　不同K 值的系统阶跃响应

下面着重讨论欠阻尼即K＝1.5 时情况。

系统阶跃响应的超调量：即峰值与稳态值之差，且与系统稳态值之比。超调量计算过程如下：

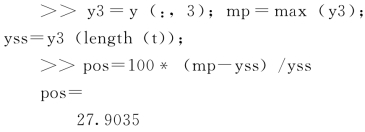
稳态误差分析：我们知道，单位反馈系统在零点处有一极点的系统为典型Ⅰ型系统，它的稳态误差eSS为零。对于斜坡响应的误差为1/KV（此处KV 为速度误差系数）。

因此，eSS＝1.33。

下面使用lSim命令去求斜坡输入响应，并且证明所得到的结果（见图8-8）。计算斜坡输入响应的简单办法是在系统闭环传递函数上再乘一个1/s，MATLAB程序8-2 为计算系统斜坡响应的程序清单。

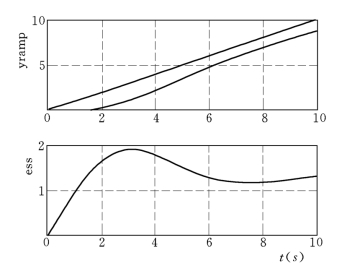
图8-8　系统斜坡响应及误差

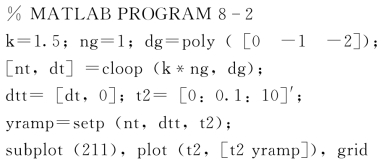
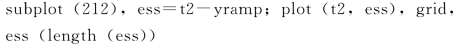
由下列命令可以验证其稳态误差：

滤波器性质：由闭环系统的波德图（见图8-5）可以看出，系统特性为一低通滤波特性。大多数系统都具有低通滤波特性，这意味着系统对高频信号具有很大的衰减特性，可通过求得随机噪声信号在欠阻尼系统中的时间响应来证明这一点。rand 命令用于将一噪声信号加入到一阶阶跃输入信号中，而lSim命令用于求解其响应。

式中，t2 是一个向量，oneS（t2）为一具有相同元素数的 ‘1’向量，而rand（t2）建立另外一个具有相同大小、元素在0～1 之间的随机数的向量、两者之和构成了一个噪声阶跃输入信号。为了便于比较，可将输入与输出绘制在同一图中，见图8-9。正如预料的结果一样，系统对高频噪声信号有一个很大的衰减作用。由于噪声信号具有0.5 单位的幅值，因此其输出信号中出现了一个0.5 单位的偏移。通常噪声信号的幅值相对于其输入信号的幅值要小得多，因此其作用几乎可以忽略。

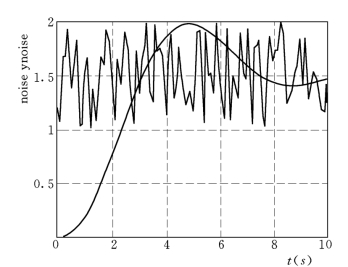
图8-9　随机噪声阶跃输入的系统响应

【例8-2】 延时作用。

延时环节应用于许多控制系统，如过程控制与制造系统等。在线性时不变连续系统中，用e－st表示延时。注意采用频率响应的方法可以较方便地分析系统特性。

e－jωT＝1∠－ωT

因此，延时环节将保持输入幅值不变，而简单地加入滞后的相角。带有延时的相角滞后会使系统趋于不稳定。如果采用波德图分析方法，则只需要在系统的相频响应中减去延时的相角，即可得到其系统的波德图。

解：

绘制系统波德图的MATLAB程序如下：

由图8-10可见，原系统具有无穷大的幅值裕量与120°的相角裕量。加入延时环节后，幅值裕量变为2dB，而相角裕量变为30°。由此可见，延时环节的作用对系统影响还是很大的。

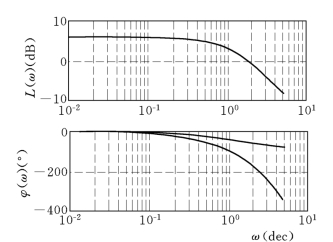
图8-10　系统加入延时环节的作用

延时环节的极坐标图可以由下式得到

G（jω）e－jωT＝[R（ω）＋jI（ω）]e－jωT

式中，R（ω）＝Re[G（jω）]；I（ω）＝Im[G（jω）]。

因此，可以计算出带有延时环节的系统的实部与虚部的频率响应。MATLAB 程序8-4 为绘制其极坐标图的程序清单。

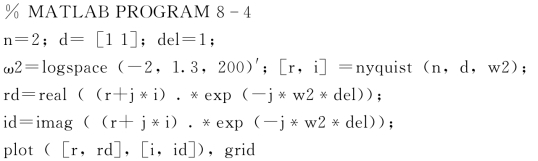
注意real、imag与exp 命令的用法。系统极坐标图见图8-11，由图可见，系统仅有很小的稳定裕量。

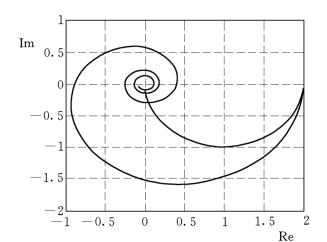
图8-11　带有延时环节的系统的极坐标图