非线性输入控制器的实现及应用

1.非线性输入控制原理

非线性输入控制器（Nonlinear Input Controler）简称NIC，是基于分段阶跃原理对系统进行控制的。分段阶跃原理的力学模型如图7-49所示。

图7-49（a）所示为一个质量为m 的重物在位置控制x（t）从a 移动到c 时，使得重物的运动y（t）从初始位置A 移动到目标位置C。图7-49（b）所示为控制位移先移动总位移量的一半，即从a 移动到b，此时重物在mg 的作用下从初始位置A 开始做摆动运动。当重物摆动到目标位置C 时，即如图7-49（c）所示，再将控制位移从位置b 快速地移动到位置c，如图7-49（d）所示。上述即为分段阶跃原理的力学解释。

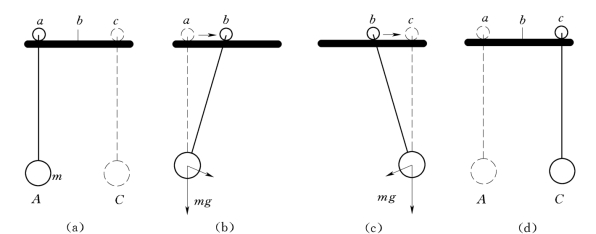
图7-49　分段阶跃原理的力学模型

从分段阶跃控制原理可以得到输入分段阶跃信号时，输入波形和目标运动波形如图7-50所示。图中的输入信号x（t）为分段输入，而系统的输出y（t）是连续的。在分段信号作用下，可以使得系统的运动不产生振荡，也没有超调量。这种控制方法，是基于线性系统的控制规律而实现的，因此可以有效地克服由于输入突变信号所引起的系统振荡与超调。

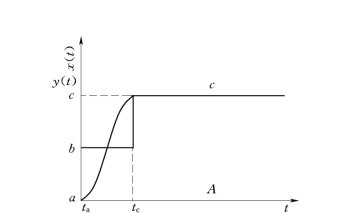
图7-50　输入波形和输出波形

2.NIC的实现电路

NIC控制电路的实现方法很多，从常规电器方法直到采用微型计算机控制都可以实现NIC控制。在此仅给出一种双分压器－定时器实现方案如图7-51所示。

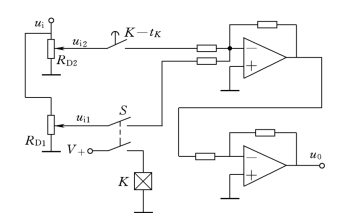
图7-51　NIC控制参考实现电路

该电路由双刀双掷开关S、电位器RD1、RD2、定时器K、相加器、反相器等组成。开关S 闭合后，输入信号ui 经分压器RD1输出第一个阶跃信号ui1至相加器，待达到定时器K 的整定时间tK 后，定时器常开接点K－tK 闭合，由第二个分压器RD2送出第二个阶跃信号ui2至相加器求和，则相加器的输出电压为－（ui1＋ui2），反向器的输出即为NIC 输出信号uo。

3.NIC的应用分析

在系统设计中，或者将系统校正为二阶系统，或者是高阶系统但是具有一对共轭复数极点。这样的系统具有衰减振荡型的运动特性，可以利用后半周期的反向特性来实现抵销，从而达到减小超调量Mp 与减小系统的调节时间tS 的目的。而衰减振荡后半周期的反向特性的抵销作用，正是可以由NIC 的分段阶跃作用来实现。总之，非线性输入控制器的有效应用是基于系统运动的基本规律而得以实现的。带有NIC控制的结构图如图7-52所示。

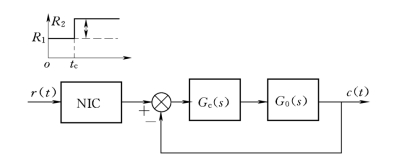
图7-52　NIC控制系统结构图

【例7-11】 已知校正后的二阶系统如图7-53所示，试采用NIC 控制方法实现阶跃信号输入时的无超调控制。

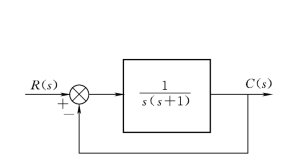
图7-53　例题7-11 控制系统

解：由于NIC控制是由分段阶跃信号实现的，所以NIC控制所需要确定的参数有两个，一个是分段阶跃信号的幅值R1 和R2 的比值；另一个是幅值R2 切换的时间tc。这两个参数可以根据二阶系统阶跃响应的超调量σ%和峰值时间tp 来确定。由于

R1＋R2＝100%，R2＝σ%R1(www.xing528.com)

所以

切换时间确定为系统的峰值时间

在本题中，系统的闭环特征方程为

s2＋s＋1＝0

则有

2ζωn＝1，ω2n＝1

解出

ζ＝0.5，ωn＝1

所以，可以确定

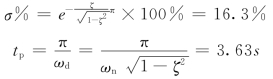
则NIC控制器的控制参数为

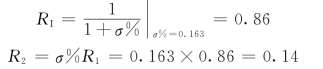
切换时间为

tc＝tp＝3.63s

NIC控制实现的无超调响应波形如图7-54所示。

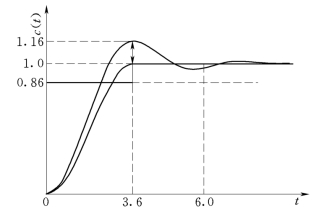
图7-54　有超调响应和无超调响应

图中的分段阶跃值分别为0.86 和0.14，切换时间为3.63S。系统响应在过了切换时间之后就进入了稳态，没有超调量，系统响应的调节时间为3.63S。

将常规阶跃响应曲线也画在坐标系中进行对比，可以看出，系统响应具有16.3%的超调量，而响应的过渡时间大约6S。

由此可见，NIC控制可以非常有效的抑制系统启动阶段所产生的超调量。上述例题虽然是按照理想情况进行计算的，但是即使分段阶跃信号的幅值有一定的误差，或者切换时间有一定的误差，与常规方式相比，非线性输入控制的方法也可以得到满意的控制效果。