PWM控制器：解决线性系统非线性问题的应用

PWM是脉冲宽度调制（PulSe Width Modulation）的缩写，就是将幅值变化的时间信号转换为脉冲宽度变化的信号的调制方法。近年来PWM控制器更多地应用于控制系统的执行装置中，用以解决线性系统控制中的许多非线性问题。

1.PWM调制的基本原理

脉冲宽度调制器的硬件电路与信号调制原理如图7-42所示。

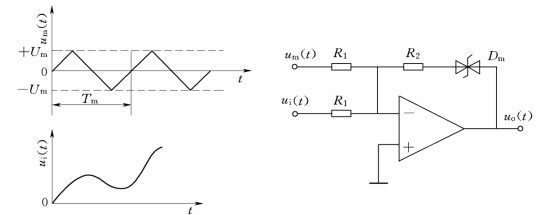
图7-42　PWM信号调制硬件电路原理

图7-42中ui（t）信号的幅值随时间变换，um（t）称为调制信号。电路是一个求和器，但输出电压的幅值有一定限制，其限幅电压为Dm 所限定的电压。当ui（t）小于um（t）时，运算放大器的输出即为正限定电压，其值为＋Um，当ui（t）大于um（t）时，运算放大器的输出即为负限定电压，其值为－Um。图7-43为PWM调制器的输出波形。

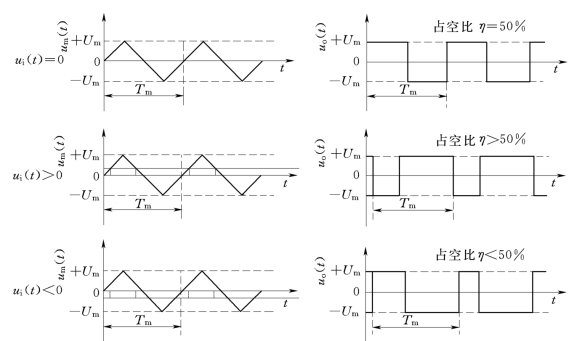
图7-43　PWM调制过程中脉冲占空比η的变化情况

由图7-43可知，ui（t）为输入信号，即被调制信号，um（t）为调制信号，PWM 调制器的输出信号uo（t）是方波脉冲，它的周期与um（t）的周期Tm 相等，方波脉冲的占空比η的大小正比于ui（t）的大小。由此我们得到如下结论：

（1）被调制信号ui（t）的幅值等于零时，输出方波信号uo（t）的占空比η等于50%，其傅氏级数展开式中直流分量等于零。

（2）被调制信号ui（t）的幅值大于零时，输出方波信号uo（t）的占空比η大于50%，其傅氏级数展开式中直流分量大于零。

（3）被调制信号ui（t）的幅值小于零时，输出方波信号uo（t）的占空比η小于50%，其傅氏级数展开式中直流分量小于零。

PWM脉冲作为控制器的结构图如图7-44所示。

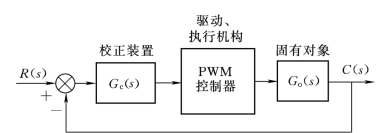
图7-44　脉冲宽度调制（PWM）控制系统

PWM控制有较好的滤除高次谐波分量的作用。所以就直流分量的传输来说，PWM控制实现的是把幅值变化转换为脉冲宽度变化，但它们的控制效果是等价的。

2.PWM控制的特点

PWM控制与线性连续控制方式相比，具有以下几个方面的优点。

（1）PWM控制方式的采用对非线性的影响具有较好的削弱作用，尤其可以克服死区非线性的影响。

幅值连续变化的时间信号经过PWM调制之后，变成幅值相等而脉冲占空比变化，即脉冲宽度变化的时间信号。因此，信号传输过程中不灵敏区的影响被减弱了，如图7-45所示。

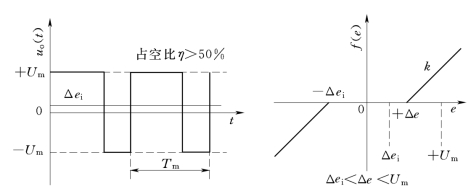
图7-45　PWM控制用以克服死区非线性

图7-45中信号占空比大于50%，其直流分量大小为Δei。若把幅值为Δei 的直流信号直接加至后面的非线性环节上，由于Δei＜Δe，则该非线性环节的输出为零。若将PWM调制信号加至该非线性环节，由于＋Um＞Δe，该小直流信号就可以传输到死区非线性环节的输出端，也就是说，小直流信号的传输是利用交流方式实现的。

该原理具有广泛的应用，尤其是各种位置伺服控制系统，应用此原理解决了系统的运动在低速下的跳动爬行问题，在此不予详述。

（2）PWM控制方式解决了功率电子驱动的功率损耗问题。

如图7-46所示，功率器件的损耗可以看成是结压降与结电流的乘积。

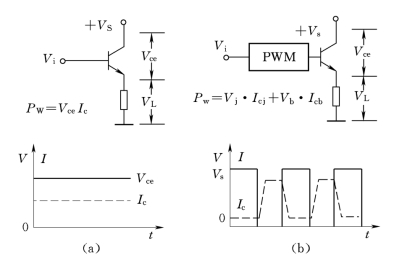
图7-46　PWM工作方式的低功耗示意图

（a）线性工作方式的功率损耗；（b）PWM工作方式的低功耗

在线性工作方式时，要保持静态时功率晶体管的c—e 结压降Vce与负载压降VL 的一定分压关系，才能保证输入输出关系的线性可调。因此，功率晶体管的功耗为

在PWM工作方式时，功率晶体管工作在开关状态，当晶体管处于截止状态时，Vce很大，接近于源电压VS，但工作电流Ic却很小，理想情况下截止电流Icj为零。当晶体管处于饱和状态时，工作电流Ic最大，但是晶体管的饱和压降Vb 最小，理想饱和压降Vb 为零。因此功率晶体管的功耗计算公式为

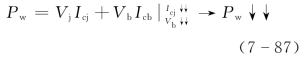(www.xing528.com)

式（7-87）所述PWM方式的低功耗原理已经广泛地被应用于电流型控制系统的驱动控制中。

（3）PWM 控制方式可以使系统的响应加速。

在PWM控制方式下，输入信号的幅值与输出脉冲的占空比成线性关系。除此之外，PWM方式输出脉冲的幅值Um 也是可以加以利用的。

采用PWM控制时，可以通过有效利用最大信号变化率，来达到使得系统的时间响应速度加快的目的，与加大系统的开环增益是等效的，展宽了系统的响应频带宽度。

例如，一阶惯性环节采用PWM控制方式，它的传递关系为

设PWM脉冲的电压为恒值UM，是所需平均电压的KM 倍，即

代入式（7-88），有

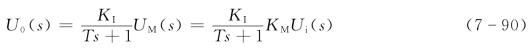
等效开环增益为

由式（7-91）可以看出，PWM控制使开环增益扩大了KM 倍，系统对于PWM方波脉冲信号响应的变化率为

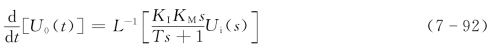
其最大变化率为

可见，PWM控制能够充分地利用最大电流变化率，且最大电流变化率分布于整个控制时段。

【例7-10】 一阶系统的闭环控制如图7-47所示，试考查PWM控制的加速作用。

解：图7-47（a）系统阶跃响应的调节时间为

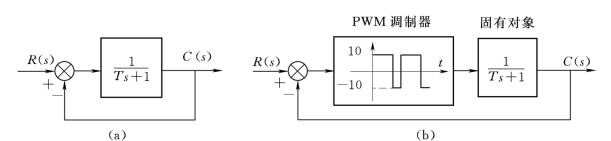
图7-47　PWM控制的加速作用

（a）一阶系统；（b）PWM控制一阶系统

图7-47（b）中PWM调制器的幅值为10，为标称值的10 倍。将该倍数折合到固有环节上，则开环传递函数成为

这相当于开环增益扩大了10 倍，因此，系统阶跃响应的调节时间为

系统的阶跃响应加快了大约5 倍。

图7-48是两闭环系统的波德图。由图可看出，PWM控制系统的转折频率大约提高5 倍频左右，所以说PWM控制展宽了原系统的频带宽度。

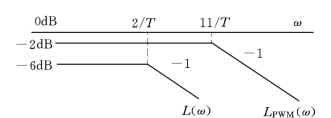
图7-48　两系统的波德图

在实际应用中，PWM 的脉冲周期Tm 的选择很重要。Tm 过大会导致频率过低，系统输出信号中的高频分量多。反之，Tm 过小会导致频率过高，会影响在一个周期内可调占空比的分辨率精度。建议可以以系统开环截止频率的5～10倍的频率作为PWM脉冲的基本频率，也可以根据实验结果来调整确定该频率。