用相平面法分析具有饱和特性的非线性系统

作出系统的相平面图，我们就可以利用相平面图进行系统分析了。尤其是对于那些具有间断特性的非线性系统，利用相平面图进行分析更为方便，如继电特性、死区特性等。

相平面图分析的一般方法如下：

（1）需要作出系统在相平面上运动的相轨迹。对于上述具有间断特性的非线性系统，其输入作用一般表示为数学上的分区作用，因此，在相平面上的相轨迹也是分区作出的。

（2）分析系统的稳定性。由分区穿越的各段构成的相轨迹，最终是收敛还是发散，表征了非线性系统相轨迹的敛散性，也就确定了该非线性系统稳定性。

（3）分析系统是否具有极限环。极限环是非线性系统独有的特征，因此，极限环是否存在、是否是稳定极限环、极限环运动区域的大小等，也就确定了该非线性系统有关自持振荡的主要信息。

最后，可以参考线性系统的性能指标来考虑该非线性系统的调节时间与超调量等。

在相平面分析时，通常将输入作用下系统的运动化为系统的自由运动来考虑。这样，x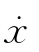－相平面就化为e－相平面。在一般情况下，参考平衡点在坐标变换下转移到原点。其方法为

系统误差的各阶导数为

因此有

将上述各式代入原方程即可得到以误差e（t）为运动变量的微分方程了，从而对应的平面为e－平面。

【例7-6】 继电型控制系统如图7-19所示，系统在阶跃信号作用下，试用相平面法分析该系统的运动。

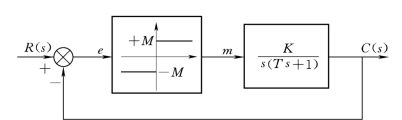
图7-19　继电型非线性控制系统

解：系统的线性部分为

非线性部分为

误差方程为

e（t）＝r（t）－c（t）

对于阶跃信号，，所以有

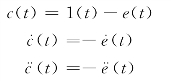
代入原方程，得到以误差e（t）为运动变量的方程为

由于m 为继电器型非线性的输出，代入式（7-34）可以得到两个运动方程。

当e＞0 时，运动方程为

等倾线方程为

这是水平线方程，因此，等倾线为布满右半平面的水平线，且α＝0 时等倾线斜率等于相轨迹斜率。

在e－平面上作出右半平面的相轨迹如图7-20所示。

同理，当e＜0 时，运动方程为

等倾线方程为

等倾线为布满左半平面的水平线。且α＝0 时等倾线斜率等于相轨迹斜率。e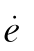－平面上左半平面的相轨迹如图7-20所示。

当给定初始条件，系统的运动从（0，e0）开始在第Ⅰ区，依照第Ⅰ的运动方程式（7-35），运动进入第Ⅳ象限，如图中实线所示。到达误差e＝0 的界面（图7-20中的A点）后，系统的运动进入第Ⅱ区。在第Ⅱ区，系统的运动服从第Ⅱ区的运动方程式（7-37）沿实线运动到B点，之后又进入到第Ⅰ区。

从相平面图的运动我们可以看到，相轨迹的整体运动是由分区的运动组合而成的。分区的边界就是继电特性的翻转条件e＝0。该系统的组合运动是衰减振荡型的，且没有极限环出现。当时间趋于无穷大时，误差趋于零。另外，从图7-20可以读到系统超调量的大小为Mp。

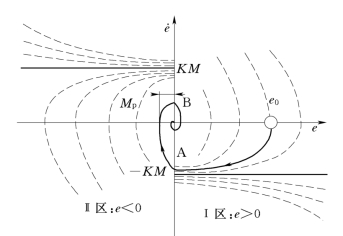
图7-20　继电型非线性系统的相轨迹

上述理想继电控制的二阶系统，虽然控制是开关型的，但是系统的运动从整体上来看与线性二阶系统的运动相类似。开关型控制器的结构与成本都要大大低于线性控制器，因此，在许多控制应用中，经常采用继电型控制方法。

但是，非理想的继电特性，将会带来其他的变化：

（1）带有滞环的继电特性会产生极限环。

（2）带有死区的继电特性会产生奇线。

以上两种非理想机电控制系统的相轨迹如图7-21所示。(www.xing528.com)

图7-21（a）中，由于滞环的存在，继电特性的切换会延迟发生，因此造成相轨迹永远不能到达相平面的原点，形成极限环，系统的运动为自持振荡型的。

图7-21　非理想继电型非线性控制系统的相轨迹

（a）继电＋滞环特性；（b）继电＋死区特性

图7-21（b）中，由于死区的影响，相平面分为三个区。在Ⅱ区内，继电特性的输出为零，因此运动方程为

等倾线斜率α恒为常数

另外，由于

方程两边作一次积分，得相轨迹方程为

相轨迹斜率恒为常数

即等倾线斜率等于相轨迹斜率，相轨迹为等斜率直线如图7-21中所示。这样，在原点邻域得相轨迹的运动会停留在死区范围内的任意一点而构成奇线，如图7-21（b）中的粗实现段。

（3）线性提前切换使继电控制系统响应加速，改善了系统的动态性能。

（4）线性延迟切换会加大系统的响应时间，甚至产生极限环或者不稳定。

继电型控制的线性切换情况的变化对系统性能的影响如图7-22所示。

图7-22中（a）为切换线e＝0 时的相轨迹。图7-22中（b）、（c）为切换线e＋ke＝0 时的相轨迹。当ke＞0 时如图7-22中（b）所示。切换线逆时针倾斜，过Ⅱ、Ⅳ象限，使得相轨迹可以提前切换，减少了振荡次数，缩短了系统的响应时间，系统的动态性能得到改善。

相反，当ke＜0 时，切换线则顺时针倾斜，过Ⅰ、Ⅲ象限，相轨迹的切换延迟，增加了振荡次数，加大了响应时间，甚至产生极限环或者不稳定，使系统不能趋于稳态。图7-22中（c）所示即为出现极限环的情况。

图7-22　切换线变化时继电控制系统的相轨迹

（a）e＝0；（b）；（c）

关于线性切换方式的实现，可以在原控制系统上增加速度反馈通路得到，如图7-23所示。

图7-23　线性切换方式的实现

因此，切换线成为

速度反馈系数ke 的大小可以调整线性切换线的斜率。当ke＞0 时为速度负反馈，切换线逆时针方向倾斜，使得继电特性可以提前切换，因此加快了系统的响应速度。当ke＜0 时速度反馈成为正反馈，切换线则顺时针方向倾斜，继电特性的切换成为延迟切换，系统的动态性能也就变差了，甚至发散。

【例7-7】 带有饱和特性的非线性系统如图7-24所示，试用相平面法作系统分析。

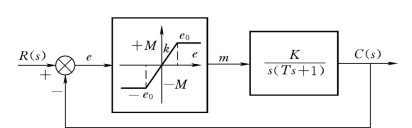
图7-24　含有饱和非线性的控制系统

解：系统线性部分运动方程为

非线性部分分为

此处m 为饱和特性的输出，代入误差运动方程即得到三个运动方程为

这三个运动方程分别表达了系统在三个分区中的运动特性。

方程（1）、（3）的相轨迹与继电特性的相轨迹相同，但是由饱和点所决定，切换位置提前，方程（2）的相轨迹为线性系统的运动。由于方程（2）的奇点性质为稳定焦点，所以最后一次进入Ⅱ区后，相轨迹不再进入其他工作区，在Ⅱ区内经有限次振荡后，最终收敛于原点如图7-25所示。

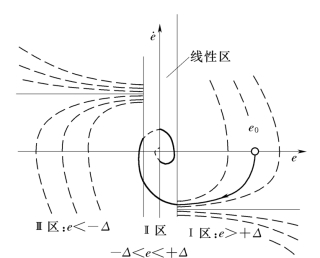
图7-25　饱和非线性系统的相轨迹

从饱和特性的相平面分析可以看到：

（1）如果系统的固有部分具有良好的阻尼特性，系统最后进入Ⅱ区后，呈现出在超调量、调节时间、振荡次数等方面均良好的动态特性，而且不产生自持振荡。

（2）饱和点的大小可以决定分区切换次数的多少。饱和点的值大，则线性工作区大，分区切换次数少，非线性振荡次数少，饱和非线性对系统的影响小。饱和点的值小，则线性工作范围小，分区切换次数增加，非线性振荡次数增多，饱和非线性对系统的影响就不可忽视。