如何用等倾线法绘制二阶系统的相平面图

由例题可以看到，只要找出x 和之间的关系，描绘在相平面上，就得到了该系统的相轨迹。作系统的相平面图时，可以利用计算机作图，或者徒手作草图。

徒手绘制相平面草图时有两种方法，即解析法和作图法。作图法有等倾线法和δ法，在此只讲述等倾线法作图，关于δ法作图，可以参阅其他书籍。

1.解析法

用求解微分方程的办法找出x 和之间的关系，从而可在相平面上绘制相轨迹。这种方法称为解析法。

当方程不显含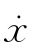时，可以采用一次积分法求得相轨迹方程来作图，即方程为

因为

将式（7-8）代入式（7-7），得

方程两边作一次积分，可得相轨迹方程为

【例7-3】 二阶系统为

作该系统的相平面图。

解：由解析法有

即

方程两边作一次积分，可得相轨迹方程为

这是一个椭圆方程，如果以为纵坐标，则在不同的初始条件下的相轨迹如图7-11所示，系统的相轨迹为同心圆。

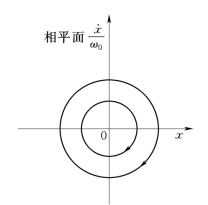
图7-11　相平面与相轨迹

2.等倾线法作图

所谓等倾线，是指在相平面内对应相轨迹上具有等斜率点的连线。

由于，将其代入二阶非线性系统方程式（7-6）得

其中，为相轨迹在某一点的切线斜率。

在相平面上，除了系统的奇点（后面要讲到）之外，在所有的解析点上，设α为常量，令斜率为给定值α，即

由此式所确定的关系曲线即为等倾线，则得到相平面上相轨迹的等倾线方程为

给定一个斜率值α，便可以在相平面上作出一条等倾线。当给出不同的α数值时，便可以作出若干条等倾线，即等倾线簇，充满整个相平面。(www.xing528.com)

线性定常系统的等倾线为过原点的一次曲线。

线性定常系统为

将代入方程有

所以有

给定不同的α值时，等倾线为若干条过原点的直线。

当线性系统运动方程不显含x 时，例如运动方程为

其中，a、K 均为常数，则等倾线方程为

等倾线为水平线充满整个相平面。

非线性系统的等倾线方程是直线方程时，采用等倾线法作图更为方便。

【例7-4】 系统方程为

试在相平面上作出该系统的等倾线。

解：将代入运动方程，得到等倾线方程为

给定不同的α值，等倾线为一系列幅值不等的正弦曲线族，在相平面上作出等倾线如图7-12所示。

图7-12 正弦函数型等倾线

作出了等倾线后，相轨迹在穿过某条等倾线的时候，是以该条等倾线所对应的斜率α穿过的。所以，系统运动的相轨迹就可以依据布满相平面的等倾线来作出。先由初始条件确定相轨迹的起点，然后从相轨迹起点出发，依照等倾线的斜率，逐段折线近似将相轨迹作出。下面以例题来说明。

【例7-5】 二阶系统为

试用等倾线法作该系统的相平面图。

解：将代入方程，得等倾线方程为

方程为过原点的直线方程，等倾线的斜率为

上式为等倾线斜率与相轨迹斜率的关系，给定一系列相轨迹斜率α的值，便得到一系列等倾线斜率的k 值，可以作出等倾线如图7-13所示。

等倾线作出后，从给定的初值出发，依照相轨迹斜率作分段折线，就可以画出系统的相轨迹如图7-13所示。

图7-13　等倾线法作相轨迹图