校正高阶典型系统期望特性的方法

首先根据给定的性指标，先建立一个典型的开环模型，即符合性能要求的“期望”频率特性，然后把它同系统的固有部分特性相比较，最后得到所需要的校正元件的传递函数Gc（s）。

这里介绍的是四阶典型系统，其开环传递函数为

对数幅频特性如图6-39所示。图中ω1＝1/T1，ω2＝1/τ2，ω3＝1/T3，ω4＝1/T4，中频段宽度为l＝ω3/ω2。

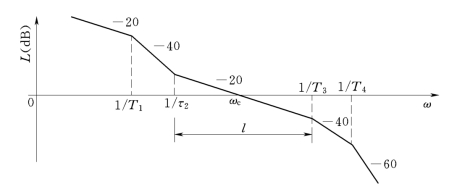
图6-39　高阶系统对数幅频特性

1.稳态指标与模型参数的关系

因是Ⅰ型系统，所以静态速度误差系数Kυ＝K，当ω＝ωc 时，则

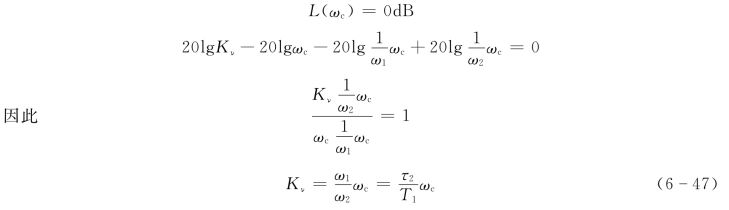
2.动态指标与模型参数的关系

按谐振峰值最小的设计原则求得其近似关系

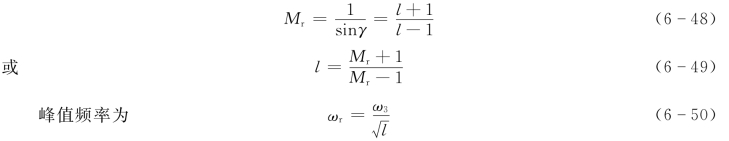
为便于利用对数幅频特性，可以这样安排中频段，使

当l≫1 时，取ω3 ≈2ωc，则

当l≫1 时，取，则

中频段的设计是很重要的，必须适当地安排各有关频率，其原则是：

（1）由快速性的要求确定截止频率ωc 的大小。根据简化经验公式决定：

（2）为保证控制系统具有良好的平稳性，要求中频段斜率为－20dB/十倍频程，且要有足够的带宽，一般取l＞10，也可按公式计算。为了查找方便见表6-2。

表6-2

(www.xing528.com)

从表中可以看出，当l＞10 以后，l 再增加时，峰值Mr 和相角裕度γ变化较小，故一般情况下取l＝10～20 即可。

（3）高频段频率ω4 的选取要有利于系统的抗干扰性能。

【例6-7】 已知一位置随动系统，其固有部分特性是

要求设计一串联校正装置Gc（s），使系统满足以下性能指标：

1）Ⅰ型系统，且Kυ≥1000S－1。

2）单位阶跃响应指标tS≤0.25s，σ%≤25%。

解：1）建立四阶开环模型。

首先画出系统固有部分的开环对数幅频特性曲线Ⅰ，为保证Kυ≥1000S－1，显然原系统不符合要求，在低频段斜率为－20dB/dec，且要保证Kυ≥1000S－1，中频段

为保证系统具有良好的快速性，取ωc＝40S－1，为了照顾系统的固有特性，简化校正装置，取，为保证中频段具有足够的宽度，取l＝14，则，取ω2＝10S－1，考虑到系统的抗干扰性与校正装置的可实现性，取ω4＝200S－1。从频率ω2 作－40dB/dec斜线，与低频段交于频率ω1＝0.6 处，得ω1＝0.6S－1。

另外，频率的值过大，将影响系统的相角裕度γ，对系统的稳定性不利。但其值过小，将在系统的闭环动态响应中，引进一个衰减很慢的动态过程分量，使动态过程延长，形成所谓的“慢爬行”现象，这是不利的。ω1、ω2 的选择要全面考虑，一般情况下，ω2选定后，ω1 自然可得。

2）检验期望系统特性的性能指标。

建立系统的开环模型是否符合性能指标的要求，需进行校验。

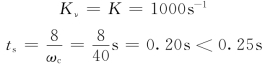
查表6-2当l＝14 时，Mr＝1.16，因此σ%＝100（Mr－1）%＝16%＜25%。

各项指标均满足要求。如不满足要求，需根据具体情况，反复修正期望特性Ⅱ，直到全部满足性能指标为止。

3）确定校正装置。

图6-40所示波德图中期望特性Ⅱ减去固有特性Ⅰ得特性Ⅲ，这就是所要求的串联校正装置。其传递函数为

图6-40　系统对数幅频特性图

该传递函数可以采用有源滞后—超前网络实现。