二阶典型系统的优化模型与校正方法

在工程设计中，经常采用二阶典型系统来代替高阶系统（如采用主导极点、偶极子等概念分析问题），其动态结构图如图6-35（b）所示。同时还经常采用“最优”的综合校正方法。二阶典型系统开环传递函数为

对数幅频特性如图6-35（a）所示。

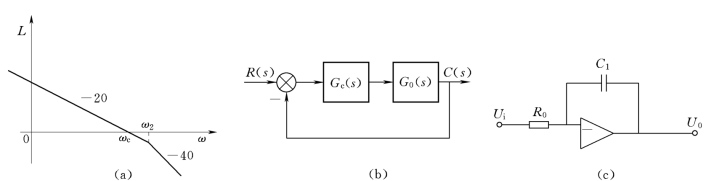
图6-35　系统对数幅频图、动态结构图和校正网络图

闭环传递函数为

1.二阶典型系统的最优模型

条件

这时从某种意义上看，其闭环频率带最宽，动态品质最好。

把代入得到

式（6-40）就是进行校正的条件。

最优模型的性能指标为

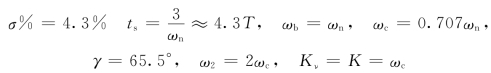
2.二阶最优模型的综合校正方法

下面分几种情况说明其思路：

（1）系统固有部分特性是一个惯性环节，即

按二阶典型系统应串入积分控制器，即

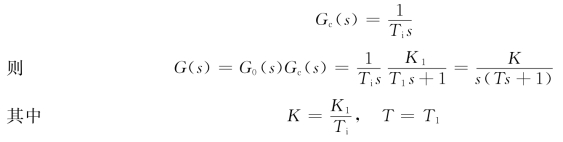
应满足最优条件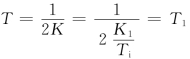，代入，即，因此Ti＝2K1T1。

可实现的电路参数Ti＝R0C1，电路图如图6-35（c）所示。

（2）系统固有部分是两个串联的惯性环节，即

可使其化成二阶典型系统，则需采用PI控制器，即

选参数时注意把时间常数大的环节消去，即

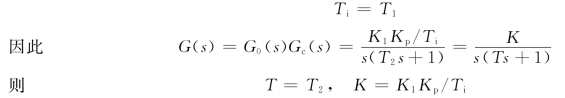
条件，，即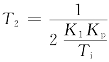，选用积分时间常数Ti＝T1，则得

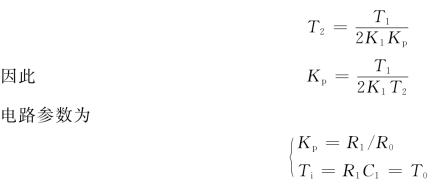
电路图即为PI网络，如图6-15所示。

（3）系统固有部分由一个大时间常数的惯性环节和若干个小时间常数的惯性环节串联组成，即

(www.xing528.com)

其中T1≫T2＞T3＞…，i＝2，3，…，n

把小时间常数合并成一个等效的时间常数，即

T∑＝T2＋T3＋…＋Tn

这样就把问题化为问题（2），可按两个串联的惯性环节处理。

（4）系统固有部分为典型二阶系统，，但不符合最优条件，遇到这种情况要根据要求的性能指标来具体地进行校正，下边分别进行论述：

1）如T1 满足快速性的要求（tS＝4.3T1），稳态精度不作要求时，只要调整K1 使之符合最优条件即可，即

2）若此时T1 满足要求，而K1 不符合要求（即稳态精度不满足指标），首先使K1 增大到K 使之符合指标要求，即

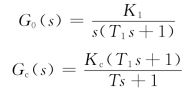
因此，使，K1 为已知，Kc 为增大的倍数，即根据指标决定的数据，亦为已知，则K＝K1Kc 为已知，所以T 即可求出。

3）如T1 不满足要求，K1 亦不满足要求，首先应使T1 满足指标要求，然后再使K1符合要求即可；或者先满足K1 再满足T1，这要根据具体情况而定。

【例6-6】 一系统开环传递函数为，如图6-35（b）所示。要求闭环系统性能指标为：超调量σ%＜5%；调节时间tS≤1S；静态速度误差系数Kυ＝10，求校正元件的传递函数Gc（s）。

解：

（1）原系统

不符合最优模型，肯定满足不了σ%＜5%，Kυ＝10 的性能指标，需进行串联校正。

（2）首先应满足

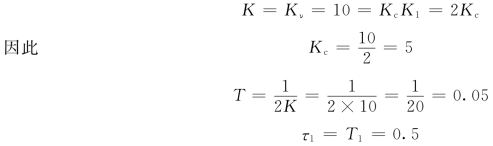
则得校正元件传递函数为

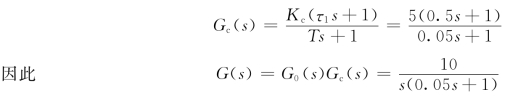
采用超前校正网络如图6-36所示，电路参数为

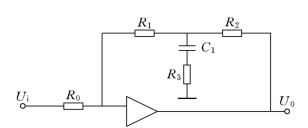
图6-36　校正网络图

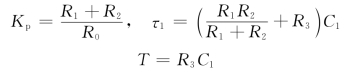
（3）验算指标。因为这是按最优模型设计的，肯定能满足性能要求，即

σ%＝4.3%＜5%

tS＝4.3T＝4.3×0.05＝0.215＜1（S）

各项指标均满足性能要求。

（4）系统固有部分传递函数

其中T1＞T2＞T3

T3 亦可以是许多小时间常数的等效时间常数，此时，应采用PID控制器

令，采用图6-19所示的PID网络，其电路参数为

二阶典型系统综合校正的方法简单，但其适应性不如高阶典型系统校正方法。因为二阶典型系统侧重于动态指标，而难以兼顾稳态性能，这就要求采用高阶模型进行校正。