开环频率特性分析及其在系统响应中的应用

对于单位负反馈系统来说，其开、闭环传递函数之间的关系为

Φ（s）的结构和参数，唯一地取决于开环传递函数G（s）。这样可以直接利用开环频率特性来分析闭环系统的动态响应，而不必计算闭环幅频特性。

时域指标σ%及tS，主要取决于闭环幅频的峰值Mm 及频带ωb，它们正处在M（ω）曲线的中间频率范围内，即所谓中频段。

时域指标eSS，主要决定于系统开环传递函数中积分环节的数目υ和开环增益K，它反映在对数幅频曲线的低频段。

下面介绍如何利用开环对数频率特性曲线在不同频率范围内的特性，来定性分析和定量估算闭环系统的动态响应。

图5-52是系统的开环对数幅频渐近特性曲线，将它分成三个频段进行讨论。

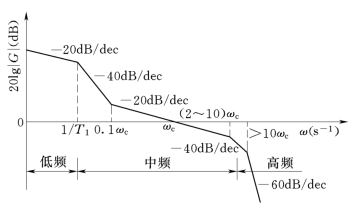
图5-52　系统开环对数幅频特性渐进特性曲线

1.低频段

低频段通常是指20lg|G（jω）|的渐近曲线在第一个转折频率以前的区段，这一段的特性完全由积分环节和开环增益决定。

低频段的斜率为0dB/dec——“0”型系统。

低频段的斜率为－20dB/dec——“Ⅰ”型系统。

低频段的斜率为－40dB/dec——“Ⅱ”型系统。

低频段的高度由K 决定。

所以，20lg|G（jω）|在低频段的特性反映系统的稳态精度。低频段对数幅频特性的形状如图5-53所示。

图5-53　低频段对数幅频曲线

2.中频段

中频段是指开环对数幅频20lg|G（jω）|曲线在截止频率ωc 附近的区段，这段特性集中反映了系统的平稳性和快速性。

下面在假定闭环系统稳定的条件下，对两种极端的情况进行分析。

（1）如果20lg|G（jω）|曲线在中频段的斜率为－20dB/dec，而且占据的频率范围较宽，如图5-54（a），则只从平稳性和快速性着眼，可近似认为开环的整个特性为－20dB/dec的直线，其对应的开环传递函数

(www.xing528.com)

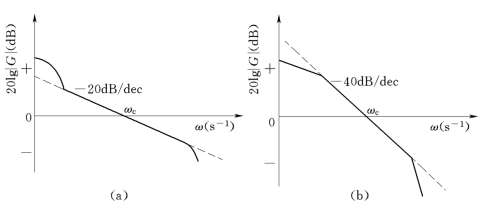
图5-54 中频段对数频率特性曲线

对于单位反馈系统，其闭环传递函数

这相当于一阶系统。其阶跃响应按指数规律变化，没有振荡，即系统具有较高的平稳性。而调节时间tS＝3T＝3/ωc，截止频率越高，tS 越小，系统快速性越好。

故中频段配置较宽的－20dB/dec斜率线，截止频率ωc 高一些，系统将具有近似一阶模型的动态过程，σ%及tS 小。

（2）如果20lg|G（jω）|曲线在中频段的斜率为－40dB/dec，而且占据的频率范围较宽，如图5-54（b）所示，则只从平稳性和快速性着眼，可近似认为整个开环特性为－40dB/dec的直线。其对应的开环传递函数

对于单位反馈系统，闭环传递函数

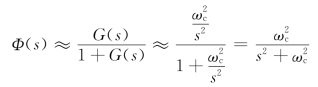
这相当于零阻尼（ζ＝0）的二阶系统。系统处于临界稳定状态，动态过程持续振荡。

因此，中频段斜率为－40dB/dec，所占频率范围不宜过宽。否则，σ%及tS 显著增大。

中频段斜率越陡，闭环系统将难以稳定，故通常取20lg|G（jω）|曲线在截止频率ωc 附近的斜率为－20dB/dec，以期望得到良好的平稳性；用提高ωc 来满足对快速性的要求。

3.高频段

高频段是指20lg|G（jω）|曲线在中频段以后（ω＞10ωc）的区段，这部分特性是由系统中时间常数很小，频率很高的部件决定的。由于远离ωc，一般分贝值都较低，故对系统的动态响应影响不大。但高频段的特性，反映系统对高频干扰的抑制能力。由于高频时开环对数幅频的幅值较小，即20lg|G（jω）|≪0，|G（jω）|≪1。故对单位反馈系统有

闭环幅频等于开环幅频。

因此，系统开环对数幅频在高频段的幅值，直接反映了系统对输入高频干扰信号的抑制能力。高频特性的分贝值越低，系统抗干扰能力越强。

三个频段的划分并没有严格的确定准则，但是三频段的概念，为直接运用开环特性判别稳定的闭环系统的动态性能指出了原则和方向。

下面介绍一个用开环对数频率特性曲线来估算闭环系统动态性能的经验公式，即

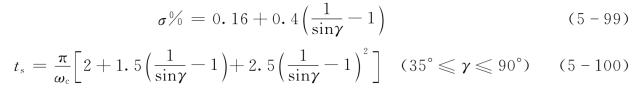
式中 γ——相角裕度。