在已知闭环系统稳定的条件下,可以只根据系统的闭环幅频特性曲线,对系统的动态响应过程进行定性分析和定量估算。
如图5-49所示闭环频率特性曲线。

图5-49 闭环幅频特性曲线
1.定性分析
(1)零频的幅值M(0)反映系统在阶跃信号作用下是否存在静差。
因为M(0)=Φ(0),则:
当M(0)=1 时,说明系统在阶跃信号作用下没有静差,即eSS=0。
当M(0)≠1 时,说明系统在阶跃信号作用下有静差,即eSS ≠0。
(2)谐振峰值Mm 反映系统的平稳性。
Mm 大,说明系统的阻尼弱,动态过程的超调量大,平稳性差。Mm 小,系统的平稳性好。
一阶系统,幅频曲线没有峰值,其阶跃响应过程没有超调。即σ%=0,平稳性好。
二阶系统,当阻尼比ζ较小时,幅频出现峰值,即
![]()
ζ越小→Mm 越大→超调量σ%越大→平稳性差。
从一个极端情况看,当Mm→∞时,即系统在某个频率ωm 的正弦信号作用下,则
|Φ(jωm)|→∞
这相当于其分母即系统闭环特征式趋于0,即有±jωm 的特征根,系统处于临界稳定状态,动态过程具有持续的等幅振荡,对应超调量σ%=100%。调节时间tS→∞。
(3)带宽频率ωb 反映系统的快速性。
带宽频率ωb 是指幅频特性M(ω)的数值衰减到0.707M(0)时所对应的频率。
ωb 高,则M(ω)曲线由M(0)到0.707M(0)所占据的频率区间(0,ωb)较宽,表明系统复现快速变化的信号能力强,失真小,反映系统自身的惯性小,动态过程进行得迅速。
对于一阶系统
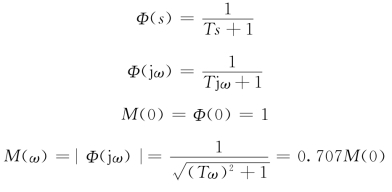
解出上式
![]()
系统调节时间![]() 。所以,ωb 越大,tS 越小。系统快速性越好。
。所以,ωb 越大,tS 越小。系统快速性越好。
对于二阶系统
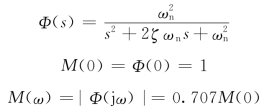 (https://www.xing528.com)
(https://www.xing528.com)
当取ζ=0.707 时,由上式解出
ω=ωb=ωn
根据调节时间![]() ,有ωn↑→ωb↑→tS↓。
,有ωn↑→ωb↑→tS↓。
若从一个极端来看,如果ωn→∞,即系统闭环幅频永不衰减,则有
M(ω)=|Φ(jω)|=1=Φ(s)
系统相当一个K=1 的比例环节,输出c(t)在任何时刻都等于输入r(t)。响应的调节时间tS 为零。
当闭环幅频的峰值Mm 不变时,系统的带宽与响应时间存在反比关系。
如果两个系统的频率特性分别为
![]()
式中,n 为任意常数。则对应的单位阶跃响应具有如下关系
![]()
式(5-95)和式(5-96)的含义如图5-50所示。
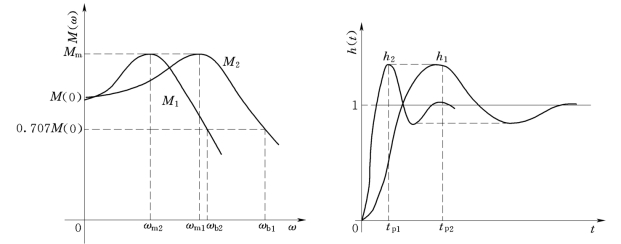
图5-50 带宽与响应时间的反比关系图
以上关系说明,系统的频率特性放宽n 倍,对应系统的单位阶跃响应就加快n 倍,这一结论可证明如下
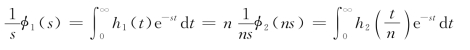
所以有
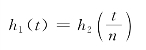
(4)闭环幅频M(ω)在ωb 处的斜率反映系统抗高频干扰的能力。
ωb 处的M(ω)曲线的斜率越陡,对高频正弦信号的衰减越快,抑制高频干扰的能力越强。
2.定量估算
利用一些经统计计算得到的公式和图线,可以由闭环幅频M(ω)曲线直接估算出阶跃响应的性能指标σ%及tS。下面仅介绍一种方法。
设稳定系统的幅频特性曲线如图5-51所示,图中:M0 即为M(0);Mm 为峰值;ωb为M(ω)衰减至0.707M0 处的角频率,即频带;ω0.5为M(ω)衰减至0.5M0 处的角频率;ω1 为M(ω)过峰值后又衰减至M0 值所对应的角频率。
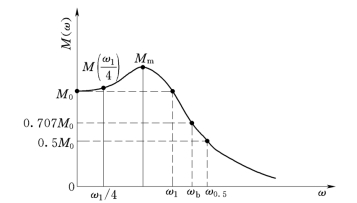
图5-51 闭环幅频特性M(ω)曲线
依上述诸值,时域性能指标的估算公式为
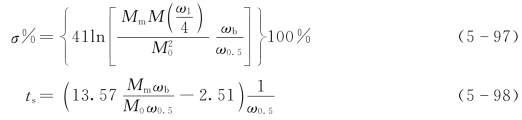
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




