对于图5-35所示系统,G(s)和H(s)分别为两个多项式之比的有理分式,设
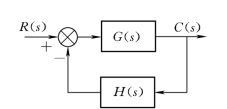
图5-35 反馈控制系统
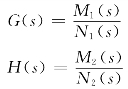
如果G(s)和H(s)没有零点和极点对消,则系统的
开环传递函数
![]()
其闭环传递函数
![]()
奈氏判据是从研究闭环与开环特征多项式之比这一函数入手的,这一函数仍是复变量s 的函数,称之为辅助函数,记作F(s),即
![]()
从式(5-75)看出,辅助函数F(s)的分子是系统闭环特征多项式,分母是系统开环特征多项式。
对于物理系统,其开环传递函数的分母最高次幂n 必大于分子最高次幂m,即n>m。
将F(s)写成零、极点形式,则

式中 zi——F(s)的零点,也是闭环传递函数的极点;
Pi——F(s)的极点,也是开环传递函数的极点。
辅助函数F(s)的特点:①其零点和极点分别是闭环和开环的特征根;②其零点的个数与极点的个数相同;③辅助函数F(s)与系统开环传递函数只差常数1。
式(5-76)中的极点Pi 通常是已知的,但要求出其零点zi 的分布就不容易了。下面利用复变函数中的辐角原理来寻找一种确定位于右半s 平面内F(s)零点数目的方法,从而建立判断闭环系统稳定性的奈氏判据。
1.辐角原理
在s 平面上任选一复数s,通过复变函数F(s)的映射关系,可在F(s)平面上找到相应的像。
设F(s)的零、极点分布如图5-36(a)所示。
在右半s 平面内任作一闭合路径ΓS(注意不能使路径通过F(s)的任何一个零点或极点),在路径上任选一点A,使s 从A点开始移动,绕F(s)的零点zi 顺时针沿封闭曲线ΓS 转一周回到A点,相应的F(s)在F(s)平面上从B点出发再回到B点,也描出一条封闭曲线ΓF,如图5-36(b)所示。
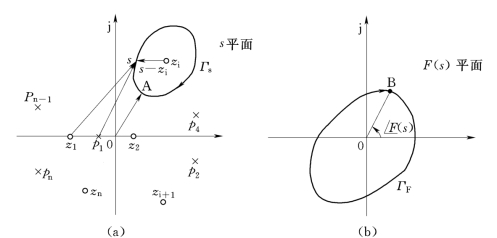
图5-36 s 与F(s)的映射关系
当s 依ΓS 变化时,F(s)的相角变化为![]() ,由式(5-76)可得
,由式(5-76)可得
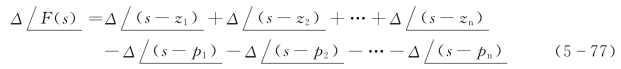
其中:![]() 表示s 依ΓS 变化时,向量s-zi 的辐角变化量。
表示s 依ΓS 变化时,向量s-zi 的辐角变化量。![]() 含义与前述类似。
含义与前述类似。
式(5-77)中,在ΓS 路径内的zi,其辐角变化量为-2π,在ΓS 路径外的zi,其辐角变化量为0。
根据图5-36(a)所示,路径ΓS 中只包围了一个zi,其余的F(s)的零、极点均分布在ΓS 之外,所以
![]()
式(5-78)表示,在F(s)平面,F(s)曲线从B点开始,绕原点顺时针转了一圈。
同样当s 从s 平面上A 点开始,绕F(s)的一个极点Pk 顺时针转一圈时,在F(s)平面上,F(s)曲线绕原点反时针转一圈。
根据以上分析,可得辐角原理:
如果封闭曲线ΓS 内有Z 个F(s)的零点,有P 个F(s)的极点,则s 依ΓS 顺时针转一圈时,在F(s)平面上,F(s)曲线绕原点反时针转的圈数R 为P 和Z 之差,即
![]()
若R 为负,表示F(s)曲线绕原点顺时针转过的圈数。
2.奈氏判据
如果把s 平面的封闭曲线ΓS 取为虚轴和右半s 平面上半径ρ为无穷大的半圆,如图5-37所示。那么ΓS 就扩大到了整个右半s 平面,则式(5-79)中的P 和Z 分别表示辅助函数F(s)分布在右半s 平面的极点和零点数,也就是开、闭环传递函数分布在右半s平面上的极点数。当s 沿无穷大半圆及虚轴变化时,F(s)在F(s)平面上绕原点反时针转的圈数R=P-Z。若Z=0,则F(s)在F(s)平面绕原点反时针方向转过P 圈,说明闭环系统是稳定的。如果R≠P,说明闭环系统是不稳定的。闭环分布在右半s 平面的极点数可由下式求得
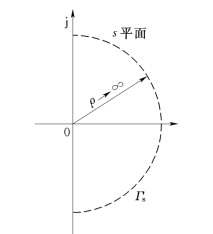
图5-37 包括全部右半s平面的封闭曲线ΓS
![]()
如果开环稳定,即P=0 时,闭环系统稳定的条件是:F(s)绕原点转过的圈数R=0。
辅助函数F(s)与开环传递函数G(s)H(s)之间仅相差1,显然,F(s)在F(s)平面绕原点反时针方向转过的圈数,G(s)H(s)平面上变为绕(-1,j0)点反时针方向转过的圈数,因此,式(5-79)中的R 可用G(s)H(s)绕(-1,j0)点反时针方向转过的圈数来确定。
由于物理可实现系统中,开环传递函数分母的最高次幂总大于分子的最高次幂,当s 在ΓS 的圆弧段取值时,通过G(s)H(s)映射到G(s)H(s)平面上的像是原点,这恰好是s 平面虚轴无穷远点映射到G(s)H(s)平面上的像,这就是说,当s对应虚轴上的±j ∞取值时,通过G(s)H(s)映射到G(s)H(s)平面上的像也是原点。这样,我们可以将G(s)H(s)中的复变量s 用jω代换,并令ω从-∞变化到+∞,(即![]() ,而G(jω)H(jω)正是系统的开环极坐标)绘制G(jω)H(jω)曲线,研究其绕(-1,j0)点反时针转过的圈数。
,而G(jω)H(jω)正是系统的开环极坐标)绘制G(jω)H(jω)曲线,研究其绕(-1,j0)点反时针转过的圈数。
当ω从-∞→0 和从0→+∞时,对应的两条G(jω)H(jω)曲线相对于实轴是互为镜像的,所以实际上只要绘制ω从0→∞变化时的曲线,这时对应的G(jω)H(jω)曲线绕(-1,j0)点转过的圈数N(反时针方向转过的圈数为正,顺时针方向转过的圈数为负)为
![]()
闭环系统稳定的条件是Z=0,则有
![]() (https://www.xing528.com)
(https://www.xing528.com)
若闭环系统不稳定,则闭环在右半s 平面的极点数为
![]()
奈奎斯特稳定判据:闭环系统稳定的充要条件是当ω由0 变到∞时,开环极坐标图G(jω)H(jω)绕(-1,j0)点反时针方向转过![]() 圈。P 为开环传递函数位于右半s 平面的极点数。
圈。P 为开环传递函数位于右半s 平面的极点数。
若开环系统稳定,即P=0 时,开环极坐标图G(jω)H(jω)不包围(-1,j0)点,则闭环系统稳定。
关于开环传递函数包含积分环节的处理如下:
当开环传递函数G(s)H(s)包含有积分环节时,则开环具有s=0 的极点,此极点分布在坐标原点上。其开环传递函数可用下式表示
![]()
由于s 平面上的坐标原点是所选闭合路径ΓS 上的一点,把这一点的s 值代入G(s)H(s)后,使|G(0)H(0)|→∞,这表明坐标原点是G(s)H(s)的奇点,为了使ΓS 路径不通过此奇点,将它作些改变使其绕过原点上的极点,并把分布在坐标原点上的极点排除在被它所包围的面积之外,但仍应包含右半s 平面内的所有闭环和开环极点,为此,以原点为圆心,作一个半径为无穷小的半圆,使ΓS 路径沿着这个无穷小的半圆绕过原点,如图5-38所示。
这样闭合路径ΓS 就由-jω轴、无穷小半圆、jω轴、无穷大半圆四部分组成。当无穷小半径趋于0 时,闭合路径ΓS 仍可包围整个右半s 平面。
位于无穷小半圆上的s 可用下式表示
![]()
下面讨论υ=1 时,令ε→0。将式(5-85)代入式(5-84)中,得
![]()
根据式(5-86)可确定s 平面上的无穷小半圆映射到G(s)H(s)平面上的路径。在图5-38中的a 点,s 的幅值ε→0,相角θ为-![]() 。对应|G(s)H(s)|→∞,φ=-θ=
。对应|G(s)H(s)|→∞,φ=-θ=![]() ,这说明无穷小半圆上的a 点映射到G(s)H(s)平面上为正虚轴上无穷远处的一点。在b 点处,ε→0,相角θ为0,对应|G(s)H(s)|→∞,φ=-θ=0,说明b 点映射到G(s)H(s)平面上为正实轴上无穷远处的一点。对于c 点,ε→0,
,这说明无穷小半圆上的a 点映射到G(s)H(s)平面上为正虚轴上无穷远处的一点。在b 点处,ε→0,相角θ为0,对应|G(s)H(s)|→∞,φ=-θ=0,说明b 点映射到G(s)H(s)平面上为正实轴上无穷远处的一点。对于c 点,ε→0,![]() ,对应G(s)H(s)→∞,φ=
,对应G(s)H(s)→∞,φ=![]() 。这说明c 点映射到G(s)H(s)平面上为负虚轴上无穷远处的一点。当s 沿无穷小半圆由a 点移到b 点,再移到c 点时,角度θ反时针方向转过180°,而对G(s)H(s)的角度,则是顺时针方向转过180°(如果系统的类型是υ型,则G(s)H(s)角度的变化是υ×180°),s 平面上的半圆abc,映射到G(s)H(s)平面上为无穷大的半圆abc,如图5-38所示。
。这说明c 点映射到G(s)H(s)平面上为负虚轴上无穷远处的一点。当s 沿无穷小半圆由a 点移到b 点,再移到c 点时,角度θ反时针方向转过180°,而对G(s)H(s)的角度,则是顺时针方向转过180°(如果系统的类型是υ型,则G(s)H(s)角度的变化是υ×180°),s 平面上的半圆abc,映射到G(s)H(s)平面上为无穷大的半圆abc,如图5-38所示。
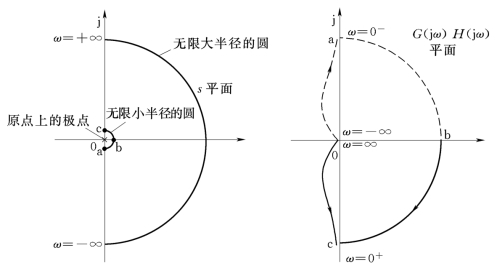
图5-38 G(s)H(s)包含积分环节时的ΓS 路径和极坐标图
开环传递函数有积分环节时,作如上处理,是将开环分布在坐标原点的极点当成分布在s 平面左半部的极点了。这样奈氏判据仍能应用。
【例5-6】 已知系统开环传递函数
![]()
试应用奈氏判据判别闭环系统稳定性。
解:1)画出系统开环极坐标曲线。
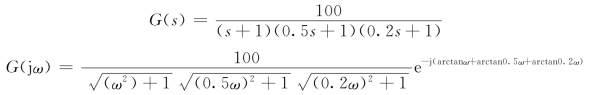
给ω一系列数值,可绘出系统的开环极坐标曲线如图5-39所示。

图5-39 例题5-6 系统的开环极坐标曲线
2)根据奈氏判据判别闭环系统稳定性。
由已知开环传递函数,可确定P=0,即开环系统稳定,开环极坐标曲线包围(-1,j0)点,所以闭环系统不稳定。
【例5-7】 已知系统开环传递函数
![]()
试应用奈氏判据判别K=0.5 和K=2 时的闭环系统稳定性。
解:1)分别作出K=0.5 和K=2 时开环极坐标曲线,如图5-40所示。
2)根据开环传递函数,P=1。
当K=0.5 时,G(jω)曲线1 绕(-1,j0)点转过的圈数为0,不等于P/2 次。所以,闭环系统不稳定。
当K=2 时,G(jω)曲线2,绕(-1,j0)点,沿ω增大的方向,反时针转过1/2 圈,正好等于P/2,所以闭环系统稳定。
从图5-40看出,当开环增益K 变化时,G(jω)曲线的形状不变,只是曲线成比例的增大或缩小。
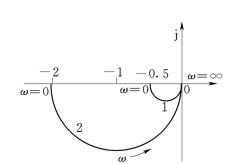
图5-40 例题5-7 系统开环极坐标图
【例5-8】 某单位负反馈系统的开环传递函数
![]()
试用奈氏判据判别闭环稳定性。
解:1)画出系统开环极坐标曲线,如图5-41所示。
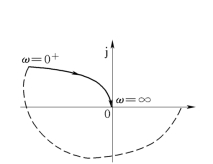
图5-41 例题5-8 系统开环极坐标图
2)开环传递函数有两个积分环节,则需要在开环极坐标曲线上ω=0+的点开始向反时针方向补画一个半径为无穷大的半圆。
3)开环正极点数P=0,而开环G(jω)曲线包围了(-1,j0)点,所以,闭环不稳定。
闭环特征方程正实部根的个数可由下式确定
Z=P-2N
式中,N 为极坐标曲线逆时针绕(-1,j0)点的圈数,由图5-41可知,G(jω)曲线沿ω增加的方向,绕(-1,j0)点顺时针转了一圈,所以N=-1,则有
Z=0-2(-1)=2
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




